I have decided to rescind this model because it is not logically consistent, the great gap was between the field equation and equations of motion. I completely accept that scalar gravity models as they appear in the literature are inconsistent with large amounts of data showing that starlight is bends due to gravity. Many of those models do have the magnitude of bending in time and space consistent with data, but since the two change in the same way, there is no bending. I will see if I can create a logically consistent model where the changes in time and space are of the same magnitude, but one gets larger while the other gets smaller. I will keep the orginal blog as is.

Newton's Universal Gravity Law was the first modern physics law that built a bridge between motions in the heavens as they are on Earth. To this day, the law remains useful. For an engineer, the only time one needs more than trusty old Newton is when the craft in question carries an atomic clock or other measurements of exquisite accuracy.

There are at least three issues with the Universal Gravity Law. One is how light is handled. The mass of light is zero. The force equation will provide the tautology that zero equals zero. The first published calculation of light bending was done by Johann Soldner in 1801 (English or the original German). I am unsure how concerned I should be that for a photon somewhere in any such calculation there will be a ratio of zero divided by zero which is not a well-defined animal. Canceling zeroes is math malpractice, no? As pointed out in comments to another blog I wrote, the answer to how much light bends in the limit of the mass approaching zero is different from when the mass is actually zero. I am at a loss for the words to describe that situation other than it does not sound good (almost inconsistent, which is a bad thing for a model). Even using the limit as the mass goes to zero answer, Newtonian gravity gets the change in absolute time right, but misses out entirely on any changes in measurements of space.

A cleaner way to see the problem of light is to consider the coupling term in the Newtonian action, the test mass m times phi the potential. For photons, there is no coupling, there is no way for the photon and the gravitational field to interact. Both will be fine without each other, and there is no bending, except of course there is bending of light and Newtonian gravity theory is flawed.

A second killer problem is that Newtonian gravity theory requires Galilean symmetry for space-time (no capacity for time to rotate into space as happens with boosts in a reference frame). The field equations have no dependence on time or derivatives of time. Any boost would shift spatial terms into time terms which are not there.

A third problem is that the law is too conservative: energy cannot be emitted by a gravitational system. Binary pulsars do lose energy in a predictable way, one consistent with the lowest mode of emission being a quadrapole instead of a dipole. There are two aspects to this test of the strong equivalence principle. The first is that a proposal needs to be simple. If one adds other fields as happens with the Rosen Bi-metric model, that usually leads to a dipole mode of emission which is not consistent with observations of binary pulsars. One good thing about an upgrade of Newton's law is that it stands a decent chance of having this quality. A second required feature is that there must be a mode of emission. In earlier blogs and comments, I had claimed incorrectly that Newton's model should satisfy the strong equivalence because I only thought of the first requirement, simplicity. With no dependence on time, there can be no gravity wave and thus no loss of energy. Newton's law is not consistent with tests of the strong equivalence principle. Few models are.

A Modern Variation on Nordström's Opening Move

After the miracle year of 1905, Einstein and any who understood special relativity could spot the problem of instantaneous change required by Newton's scalar gravity theory. Many other people have tried to construct scalar theories, and as can now be expected, there is a list of models on wikipedia. Typical efforts involved keeping the flat Minkowski metric while playing with potentials and time derivatives.

One of the first efforts was by the Norwegian physicist Gunner Nordström. For a complete analysis of that effort, read John Norton's "Einstein, Nordström and the early demise of scalar, Lorentz covariant theories of gravitation", good but not light reading at 74 pages. Start with the Newtonian field equations:

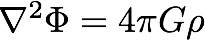
Rho is the source of the gravitational field, the mass density.

Nordström made the obvious first move: if time dependence is needed, add a couple of time derivatives.

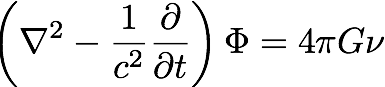
where nu is the rest mass density which is invariant under a Lorentz transformation. Why the change in the transformation properties of the source? The operator is the negative of a D'Alembertian which transforms like a scalar operator. Since the potential is a scalar, the right hand side must also be nothing but scalars.

What Nordström proposed for the rest mass density was the Lorentz invariant trace of the stress energy tensor. Before the eclipse experiment in 1919, Nordström did not know that bending of light was a requirement of any gravity model. In a previous discussion, a consensus was reached that from a modern perspective, Nordström's proposal is certain to fail to bind to the electromagnetic field whose trace is zero. If the EM field does not bind the gravity field, then there will be no bending of light which is plain old wrong. Light could bind to gravity if the source was a contraction of the complete stress energy tensor.

I believe Einstein's modus operandi was to guess field equations based on his intuition, a fine method for someone that skilled in the theoretical physics craft. The modern approach is to write down an action.

My opening move is to write the scalar 4D action ("s4D") for the field equations:

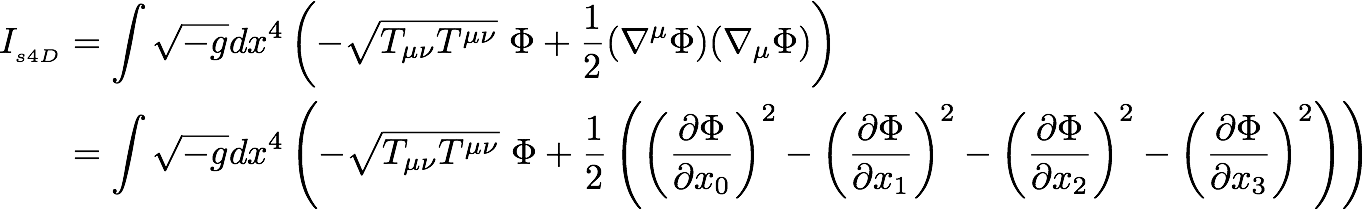
This action has Lorentz symmetry instead of Galilean symmetry, a significant upgrade from the Newtonian action. An EM field would necessarily be included in the interaction term. Note that does not mean at this point that one can say what will happen to the path of light in a gravity field. That will depend on the equations of motions for the scalar 4D model.

Apply the Euler-Lagrange equation to generate the field equation (note that is singular, there is only one scalar field and thus one field equation):

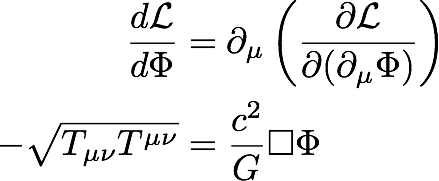
The box is the symbol for the D'Alembertian operator. Note: the operator does get considerably more complicated in curved space-time, but let's skip those details. The form of the scalar 4D field equations is strikingly similar to the Maxwell equations written in the Lorenz gauge. In both cases, a D'Alembertian operator acts on a potential which is equal to a source. The scalar 4D gravity model only has one field equation in contrast to the four for Maxwell. In the linear Maxwell field equations, the 4-current density and 4-potential both have 4 degrees of freedom. In the scalar 4D action, a complex stress-energy tensor is contracted down to a scalar which could make the field equation nonlinear. I acknowledge that the scalar potential may appear to be too small a house, but will work in this small space for now. A justification for the striking similarity between Newton's Universal Gravitational law and Coulomb's force law is now apparent.

The Simplest Solution

There is an unending list of solutions to a 4D wave equation, all depending on the boundary conditions. Dynamic solutions are simple to dream up with this wave equation. One goal of my recent blogs is to find some competition for general relativity. Therefore I will use the same constraints as apply to the Schwarzschild solution of general relativity: outside a static source that is spherically symmetric, non-rotating, and uncharged. What this accomplishes is to pack all the energy density of the source into the T₀₀ term of the stress-energy tensor in a simple form. The solution looks down right Newtonian:

The constants can be determined in the next section.

Equations of Motion for a Test Particle

An issue I puzzled over was what would it mean to say a proposal was "pure geometry"? For general relativity, the starting place is the Riemann curvature tensor. That is composed of derivatives of a metric that transforms like a tensor. The Hilbert Lagrangian has the contraction of the contraction of the Riemann curvature tensor, known as the Ricci scalar and the stress-energy tensor.

What is a core message of general relativity? Space-time is curved. Test particles follow geodesics. Here is the action to use for a test particle with mass m in flat space-time, a path parameterized by lambda, and no external force:

Small note: I am glossing over an issue here, how to write this in a manifestly covariant way, choosing Euclidean orthonormal coordinates and bunching a 3-vector together. At least I have confessed my sins to keep the equations in a simple form.

Worry sidebar: I sent a large amount of time worrying about the test particle's mass m above. Aren't I set up to fail in the case of a photon with a mass of zero? Am I repeating a mistake I made before with the interaction term? Well, that is not the interaction term, it is the inertia term. The reason there is no interaction term is due to the assumption that this is a test mass with a trivial amount of mass. This is only about how the trivial test mass moves.

Apply the Euler-Lagrange equation to derive the equations of motion:

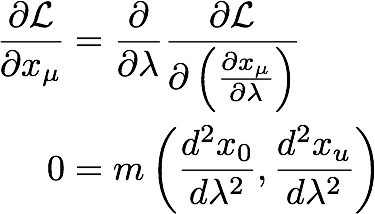
There is nothing going on, so there is no acceleration, and the velocity is constant.

In curved space-time, there is no acceleration, but the velocity is not constant. In free fall, you feel free, not heavy. Jump on a scale during free fall and see all your weight disappear, even if your mass is unaltered. Yet someone watching you fall can record changes in your velocity. If one requires an action without any acceleration, it must have the same structure as the action for flat space-time (and reduce to it when there is no gravity). I propose the following gravity-dependent transformation of the velocity:

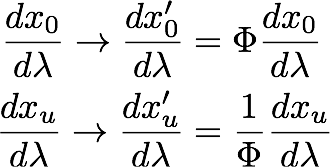
Notice the unusual way the scalar field couples with the 4-velocity. What's up with that? Shouldn't a scalar field simply change the scale of the 4-velocity? That is what happens with every scalar gravity proposal I have come across. Changes in time caused by the gravitational field are the same as changes in space. As such, all scalar gravity proposals predict no bending of light, in "violent disagreement" with experiment. Such a characterization is imprecise: the magnitude of the changes in time and the changes in space may be correct, but because they are both getting smaller or larger together, there is no bending. Recall the bigger picture of an action: a variation of the action should reflect how Nature works. In a gravity field, space-time is curved, meaning measurements of time and of space are not like they are in empty space-time.  Let me quote from an earlier blog of mine:

"The marriage of space and time is tense. They have different units. A factor of c is required to compare the two (you choose who gets the c). In flat space-time, one can contract a space-time vector and get a number that all inertial observers agree upon. That calculation grants positive values to one partner and negatives to the other (you choose who bears the minus signs). The difference in signs has major consequences to the outcome of special relativity.
What happens to space-time due to gravity was unexpected. In the contraction of a space-time vector, the previous constant values of plus and minus one were changed to dynamic values. The dynamic value was the ratio of gravitational source mass to distance. Just as important, what happens to measurements in space is approximately the inverse of what happens to measurements in time."

At this point the constants can be determined. The second constant k₂ must be unity so when there is no gravitational field one gets back the velocity in flat space-time. It is known experimentally that in a gravity field, the dynamic term in front of the time term gets smaller while the one with the space term(s) gets larger. The velocity transformation proposed here demands the potential is dimensionless. For a static, non-rotating uncharged, spherically symmetric source:

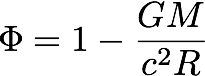
The action has the same form as before, with primes to indicate the transformation. There is no acceleration, so here are the constants of motion:

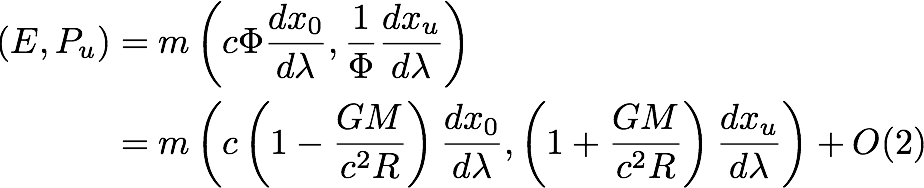
Calculate how much bending of light is predicted by the scalar 4D model. For light, the energy will equal the momentum. Solve for the deflection velocity:

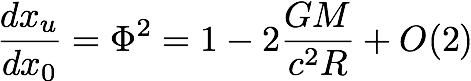
Here I can lift text from an earlier blog.

"Consider a photon flying by the Sun, setting z=0:
The total transverse deflection will be the integral over all of x of the derivative of the velocity with respect to y.


There remains a historical debate about how good the initial data was for light bending during an eclipse.  Work done by researchers at the Haystack Observatory a few miles from my home using radio astronomy has confirmed that gravity bends light precisely this amount to first order.  A measure to second order is currently beyond our reach."

There should be a discussion about whether the action is well-formed (something like manifestly covariant, but I am unsure of the jargon). The way the scalar gravity field couples to the 4-velocity in Cartesian coordinates is:

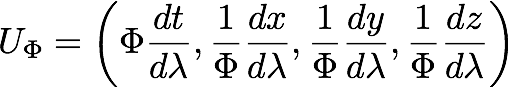
In spherical coordinates, the gravity from a point source only changes the radial component:

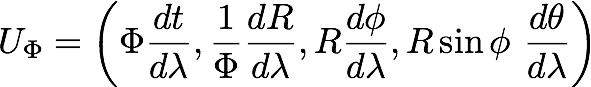
The details of the coupling of the scalar field are connected to the choice of coordinates, but those details can be figured out. I know a similar kind of thing happens when writing the Schwarzschild metric: all the change can be packed into dR in spherical coordinates or spread out over dx, dy, dz in Euclidean coordinates. Since this proposal is a coupling of a scalar field to the 4-velocity instead of a metric, it is not exactly the same but may share enough similarities to be OK.

I will proceed assuming this is not a deal breaker for readers.

Dynamic Intervals

Is there a way to view the scalar 4D model as a metric theory? No. A symmetric, rank 2 tensor has ten degrees of freedom, and a scalar model has but one. There is a way to view the scalar 4D model as having a "dynamic interval" (a phrase I am making up to label this situation), but some care is required in viewing it this way. Write the action for the equations of motion like so:

This is good because the displacement velocity can be calculated based on the "metric" like so:

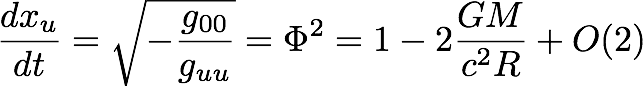
This is the same deflection velocity as before, so gets the same light bending.

Care is required in applying Euler-Lagrange. If one jumps in and takes the derivative with respect to the velocity, then the constants of motion depend on the square of the potential and inverse. That predicts twice the amount of bending than is measured, all with the same action so is internally inconsistent. The problem was taking the derivative of the Lagrangian with respect to the velocity in flat space-time. The proposal is internally consistent if one uses the transformed velocities (a Phi in just the right place).

Harder Tests to Pass

First and foremost, it would be nice if people commenting on this blog voiced their opinion on whether they think the scalar 4D model as detailed above does pass the light bending tests to first order. I have an established record of rescinding models, albeit I don't go down without some struggle. I have been slow to post this blog because I do want to be right. That could be considered a big deal since all other scalar models I read about predict exactly zero bending of light and so are wrong.

For the alpha-zeta Parameterized Post-Newtonian formulation, there are ten parameters. In GR, gamma and beta equal unity while the rest are zero. It is clear to me I don't have the intellectual horses to go through the 9 step process described on the wiki page to determine the full set of parameters. Yet it is also clear this model is considerably simpler than GR. There are no odd parts to mess up energy or momentum conservation. Presuming a simple map to this 10 parameter world, the scalar 4D model has gamma equal to one but beta equal to a half.

Later on that wiki page, it is claimed that two types of tests have determined the value of beta is equal to one. The first to 3 in 10^-3 is the perihelion shift. I did the perihelion shift for Mercury in a blog. At no time did I use beta. Does anyone know why a perihelion shift calculation would put a restriction on the value of beta in the PPN formulation?

A second justification for beta equaling one is the Nordtvedt effect, a violation of the strong equivalence principle (to 2.3 x 10^-4). Tests of the strong equivalence principle are the hardest for a proposal to pass. Recall the weak equivalence principle requires the inertial test mass is exactly the same as the passive gravitational mass. Just like Newton's proposal, the scalar 4D model works well with the weak equivalence principle. The strong equivalence principle requires that gravity is exclusively about a dynamic metric. For example, binary pulsars lose energy via gravity waves at a rate consistent with the lowest mode of emission being a quadrapole (picture a wobbling water balloon). A dipole mode of emission would dissipate energy faster than observed. I have argued above that this scalar 4D proposal could be viewed as a dynamic interval model, a phrase I made up to indicate it cannot be a full fledged metric model but does share a tested property of metric models.

At this initial point of development, I cannot write down the energy loss predicted by the scalar 4D model. A binary system is rotating and not a point source, so a different potential is required to describe the system. There are plenty of wave solutions to the 4D wave equation (not that I am too familiar with the subject).

Gravity Probe B provides tests for two effects. The first is the geodetic effect (or de Sitter precession). This is caused by taking something with a vector quantity - in this case the angular momentum of a gyroscope - and moving it around a point source of gravity. It is a first order effect in terms of the source mass, so the scalar 4D proposal should make the same prediction as general relativity.

Frame dragging, or the Lense-Thirring effect, involves a gravitational source that has angular momentum. At this initial stage of the scalar 4D model, I can imagine that angular momentum will go into the stress energy tensor, but don't know what the potential solution in that case would be. It is an open and important question to address.

The Big Picture

The scalar 4D model tries to be simple, but not too simple like other scalar gravity models. The key complication is how the scalar field couples differently between time and space. The scalar 4D model makes the approximate inverse relationship between the measurements of time and space exact.

What is the scalar field? I think of it as a dynamic history of stress-energy in the Universe: what has happened where, as seen from every point in space-time. What is most important are the local sources of stress-energy. In my case, that would be the Earth, the Sun, and the Moon, in that order. It reminds me of Mach's Principle, made more local and precise. To quote the wiki:

A very general statement of Mach's principle is "Local physical laws are determined by the large-scale structure of the universe." (Hawking and Ellis)

The variation I see in the scalar 4D proposal goes like this:

Local physical laws depend most strongly on local stress-energies, but all stress-energies in the Universe count, nearly all of which will never be detectable because they are so trivially small.

Everything goes into the contraction of the stress-energy tensor. This makes the equations of motion non-linear, a good thing.

Epilog

The Norwegian Magnus Carlsen was recently crowned world chess champion. I am a casual fan of he game. A comment he made stuck with me (source, NYTimes magazine) He said in preparing for the match, he studied opening theory. He could have focused on other parts of the game or his opponent. Instead he knew tha the initial moves set up all the possibilities that followed.

The biggest problems in physics today involve gravity: a stable, uniform start to the big bang, the acceleration of galaxies going on now, and the motion of stars within galaxies. The initial effort to make Newtonian gravity consistent with special relativity has been largely ignored, worthy only of a page long problem in Misner, Thorne, and Wheeler. I hope this re-examination of scalar gravity from a modern perspective may create a new line of attack on gravity problems because solving the scalar 4D field equations is far simpler and possibly relevant to large scale cosmology where the system is not static and non-rotating.

Note to commentors: please stick to the topic at hand, the scalar 4D gravity model.  I reserve the right to delete your comments and will do so after leaving my own comment as to why.  If you have a great solution to a problem, congrats, blog about it on this website, just not in this particular blog.