In this blog, John Wheeler's delayed choice thought experiment will be explained. The idea briefly is to ask if a single photon goes down a specific path or if the solitary photon goes down two paths so it can interfere with itself. In 2006, the thought experiment was made real by Alain Aspect and his collaborators. The paper provides the simple equations I was able to use to make quaternion animations of the process. The reader will be able to see animations of quantum interference for the first time.
click or skip this reading of the blog
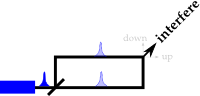
Here is a sketch of John Wheeler's nightmare:
The intensity of the source is adjusted so that it emits one photon at a time. The photon comes to a beam splitter. The solitary photon can either stay down, or turn and go to the up path or perhaps the silent solitary one decides to go on both paths as part of a plan to create an interference pattern (photons are devilishly clever). At the detector box, the experimentalist makes a choice: see if the photon took the down path, or the up path, or both paths as would be needed to see an interference pattern. The decision about what type of measurement to do is delayed until after the photon has passed by the beam splitter (technically, a spacelike separation is required). Wheeler argued that the odd logic of quantum mechanics demands such schizophrenic behavior.
Side bar: The single photon red herringWheeler's thought experiment was made real by Alain Aspect and his collaborators. The paper was fun to read and reread. I think the experimentalists got it right. Here is the entire abstract:
Intensity has never been an issue in quantum mechanics since the day Einstein explained the photo electric effect. People will nod along with the statement that intensity is not relevant to quantum processes. The consequence of the statement is that lowering the intensity to one photon a day does not change an effect except to slow the rate the experimentalist collects data. Water molecules hold hands using hydrogen bonds, so water waves are changed by intensity. Photons are isolationists, whether as solitary skaters in this experiment, or if sent as a swarm of a billion a second. The photons never hold hands or work together. Looking at a quantum effect one photon at a time is a red herring. People love their herrings and will defend their right to focus on the fish. I intend to swim on by.
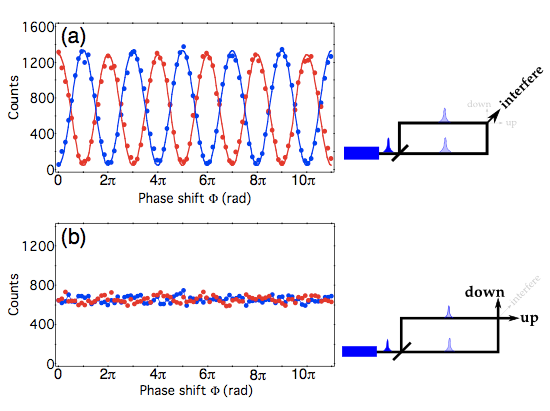
ABSTRACT: The quantum "mystery which cannot go away" (in Feynman's words) of wave-particle duality is illustrated in a striking way by Wheeler's delayed-choice Gedanken Experiment. In this experiment, the configuration of a two-path interferometer is chosen after a single-photon pulse has entered it: either the interferometer is closed (i.e. the two paths are recombined) and the interference is observed, or the interferometer remains open and the path followed by the photon is measured. We report an almost ideal realization of that Gedanken Experiment, where the light pulses are true single photons, allowing unambiguous which-way measurements, and the interferometer, which has two spatially separated paths, produces high visibility interference. The choice between measuring either the 'open' or 'closed' configuration is made by a quantum random number generator, and is space-like separated -- in the relativistic sense -- from the entering of the photon into the interferometer. Measurements in the closed configuration show interference with a visibility of 94%, while measurements in the open configuration allow us to determine the followed path with an error probability lower than 1%.
With the information provided so far, I don't think this story can make sense. People defend the idea that this story must be accepted as is, after all it is supported by the following data from the paper:
This situation reminds me of something I learned about illusion in the film "The Prestige". That was a great film by the way, one that has to be watched two or three times before you get it. An illusion has three parts:
- The Pledge
- The Turn
- The Prestige
In quantum mechanics today, I feel we must live with the Turn. People who study and know some of the vital experiments in quantum oddness like the delayed choice experiment will tell you that is the way, accept that you cannot understand. A small circle of fringe folks will holler about their own approach, one which shows no understanding of the Pledge or Turn of quantum mechanics. A real illusionist would know exactly where the answer was placed. I put the answer in plain English, but surrounded it with words that would make the reader focus on a different subject. It was in the illustration, but let me now supply some detail:
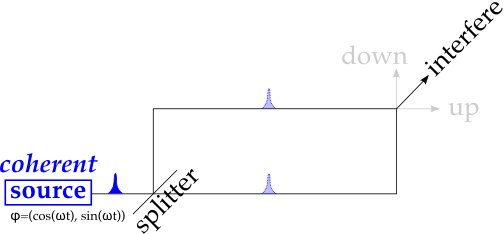I mentioned the source was coherent, but only in the context of intensity. The math of the source is treated as ordinary, even if it isn't.The up/down path detector is another herring, albeit more tempting given the name of the thought experiment. No matter what the source is, we can detect if it went on one path or another after a beam splitter. That is not a mystery. What needs to be understood is the interference for a non-interacting particle of a coherent source.
The source is so not random. Write out the wave function that would account for both ports, the complete picture:
Take the norm in order to calculate the probabilities of being in port 1 or 2:
This is unity as it must be. Observers, sitting as they do at the spatial center of their own Universe (0, 0, 0), get probabilities of seeing an event from the source by taking the norm.
Let's use the quaternion animation software to look at the amplitude of the wave function as is, equation 1, even though no one can see it.
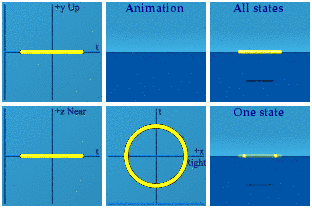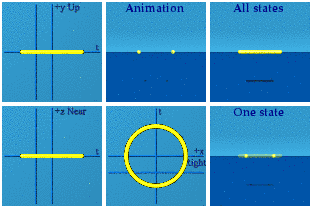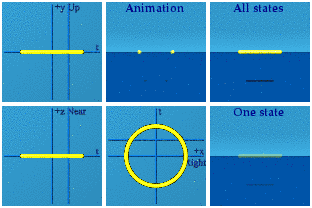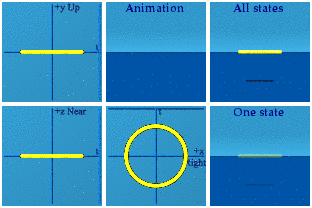
The animation has the symmetry U(1), a unit circle in the complex plane of Right-Left+time.
The animation reveals a problem with the visualization. When the phase shift is introduced, it will all be in the x direction. That shift will be darn near impossible to notice. To aid visualization, take the shift in x, and also create a corresponding shift in y. This spreads out what is happening along x.
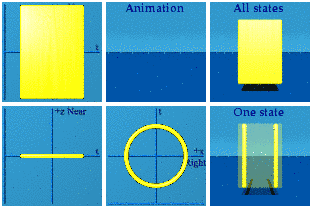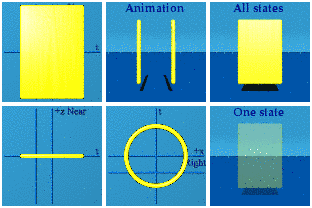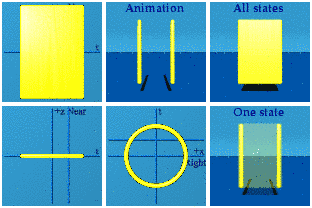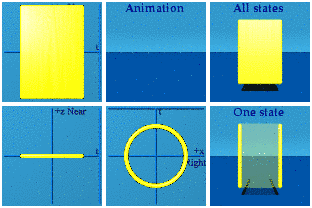
Two walls collide. Is it possible to follow one value of the phase? Again we are not being physical because individual photons cannot be marked in red, but the software can do the job:
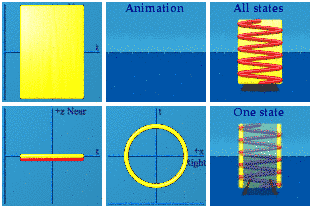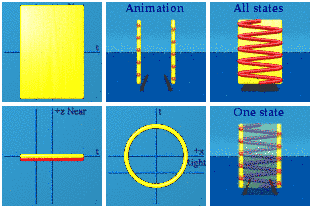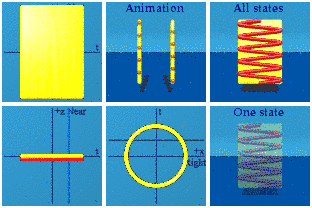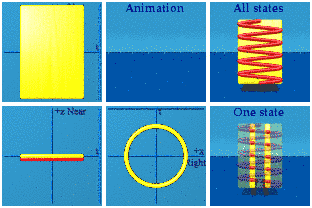
Why are there so many points in this animation? Because every point in spacetime can be mapped to this unit circle.
Label the two paths A and B. A is never shifted, B is shifted anywhere from phi = 0 to 10 pi. The data in figure 3 of the paper involves 4 calculations:
A* B - interference (3a)
B* A - interference (3a)
A* A - no interference (3b)
B* B - no interference (3b)
We can see the lack of ambiguity for the no interference case. The first two are going to be more complicated. For a fixed value of phi and omega = 1, vary t and plot:
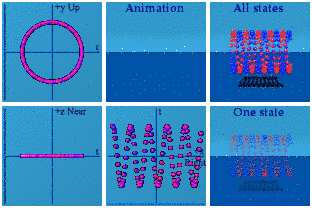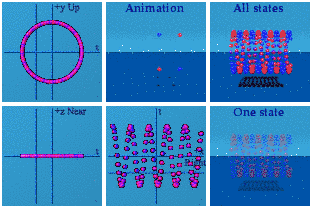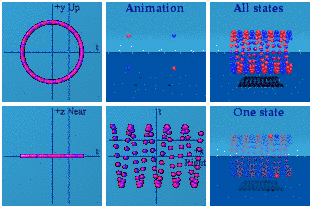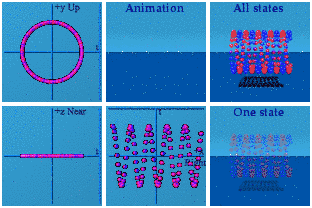
"Animations of equations 4&5 with additional shift"
This is what quantum interference can look like: the combination of three complex plane images: a straight line, a circle, and something sinusoidal. No wonder this is tricky!
(one technical detail: for the way my software is designed, I had to swap the roles of x and y, as you can tell since the circle is now in the ty plane instead of the tx plane. A bigger and smoother version of this animation is available).
I am not going to market these images as trivial to understand as that would mock any earlier efforts to have a visual interpretation of quantum interference. Instead I can point out why these images are a challenge. Time is a scalar, space is a vector. In quantum mechanics, the scalar is not a dull, monotonically increasing function. Instead, time toys with space, but mapping it back into the same space, thus hiding its hand. I needed to take what was only happening between time and one dimension of space and use another dimension to get a better handle on what was happening.
"What does one plus equal?" That is good English, math gibberish. "Did the photon go on the up or the down path?" While the question is perfect English, its is a poorly formed question for quantum interference. Poorly formed questions can never be answered. "Was there a photon at this location and at this time?" is a well-formed question. If you know exactly when a photon is seen, then a second prior to being detected you can make a statement about where it was, no matter what detector was used. Say the beam splitter was 2 light seconds away from the detector. Then there is a 50-50 chance the photon was at the half-way point of the up or the down path. If the down detector saw the photon, then the photon was at the half-way point in the down path. Notice I said both time and space locations. The photon was not in some arbitrary place along the down path a light second before detection.
What can be said if the interference detector was used? If the interference saw the maximal constructive interference, then one light second before detection, the photon was a the half-way point between either up or down. If the interference was at the maximal destructive point, then there was definitely no photon at the halfway point in either branch. For interference value between these two extremes, it sets the odds on a photon being at the halfway point a light second before being detected.
The coherent source is exceptionally well organized. It is the exquisite organization of the source that one sees in the interference pattern. Let messengers from the neat source house of particles travel down two paths of different lengths, and the resulting pattern looks like interference. The emissaries have no need to interact with each other, the proverbial bump into each other.
From my perspective, the height of absurdity in theoretical physics today are those trying to work without time. No doubt they think the delayed choice experiment is on their side. The event of the beam splitting and the choosing the type of detector is spacelike separated (a feat that was technically a great challenge to accomplish). A physics illusionist would point out that spacelike separation is a calculation done on two events in spacetime.
The results look rational, the visual part of my brain is happy.
Doug
Snarky puzzle: Supersymmetry has superpartners to build super friends between particles that take different amounts of time to jog around a circle. Animate this:
Notice how the tx takes 4 pi to get back to go, ty needs 2pi, and tz zips around in pi radians.If you like a three-way as much as I do (in theory at least), please discuss.
Google+ hangout: 11:00-11:45pm Eastern time, Tuesday-Friday. http://gplus.to/sweetser
This could be an efficient way to exchange a few ideas. If you have a question or two, hangout.
Bet against the Higgs being found,
Comments