The hypercomplex gravity and unified GEM Lagrange densities was wrong.
Nice clear admission of error, so rare these days. My critics think my fix remains wrong, so you will have to be the judge. Skepticism is a good thing. Here is the fix:
The conjugate operator is the *, basically I am removing a mirror. As much as is practical, I will go through my 30+ blogs and make the correction (should not be many posts). I have stopped the global sales of all t-shirts since the errant conjugate appears on the back. The redesign is complete, but new shirts have not been printed.
click or skip this reading of the blog:
To a fault, I have a hope that my equations will be super similar to those of EM. The current coupling term and field strength tensor of EM are invariant under 3D rotations and boosts. When I started to work with hypercomplex products, I wanted them to have that property too. It was easy to do for the current coupling term - that is why I hung a conjugate on the J. Nice, simple, direct. There are conjugates needed for the field strength.
What I did not calculate was how the hypercomplex field equations transformed under 3D rotations and boosts. Why not? There turns out to be a mountain of detail in such a calculation. I did try to do it, but did not complete the effort. That happens. So what I did since I didn't know the answer was to ask a snarky puzzle question about it, to force myself to answer the question.
Several sharp readers could see what the answer was: the hypercomplex field strength tensor was not invariant under 3D rotations and boosts. It did take me ten days to do my own effort and confirm their observations. All well and good.
Not really though. If one term in a Lagrange density is invariant under a Lorentz transformation and another one isn't, that is a problem. I actually did not spot that internal inconsistency at the time.
Let's go back to two things I did derive. I got Gauss's law for EM:
In the static case, this reduces to:
Looks old school.
Here are my hypercomplex gravity field equations:
In the static case, this reduces to:
This one appears in Misner, Thorne, and Wheeler as a good old field theory for gravity (not my invention). Not much different between those two forces or those two equations except a sign. Like charges repel for EM, but attract for gravity.
Both of those equations have similar, but not the same solutions. It is a really cool cancellation that solves the vacuum equation, when there is no rho. What is darn tricky is showing that the q/R solution works when there is a rho. It does work, if and only if rho is negative. That's how it goes in EM.
To get a solution for the gravity equations takes more thought. There is a wonderful article on the subject by Kevin Brown, "Why Maxwell Couldn't Explain Gravity". It is well worth the read. Maxwell was so sharp. He wanted to treat gravity as something that had positive, definite energy. Yet the phi needed a minus so that like charges attract. He realized that by the rules of integral calculus, one could staple on a HUGE positive value to the phi to keep it positive overall. Unfortunately, he was not able to justify that move, so he remained puzzled about this subject to the end of his days.
What Brown argued was the Schwarzschild solution to the field equations of general relativity resolved this issue. The first two terms of the Taylor series expansion of the square root of g00 as R goes to infinity could be used to define phi:
Almost no one includes that big factor of 1. I call this this Ed Miksch big factor of one. He is an older guy, going to APS meetings, talking about negative mass. Personally, I think he is channeling the issue Maxwell knew and solved but could not justify until after his death, with the work of Einstein and Schwarzschild.
So to my eye, I think I have delivered to the Science20 community field equations where like charges attract. That has not changed at all, even with the above admission of error which does not alter the first field equation.
The super tricky thing is that everything absolutely has to fit in together perfectly. That phi up there, that is the one I have to use in whatever force equation I derive. I did say I had never done that before right? Oh, I had done the EM Lorentz force lots of times, but not one for gravity.
People are so much more comfortable with forces than field equations. Forces appear so direct, good old pushing and shoving. There is a direct link between the force and field equations. This was in the Bible according to Purcell, "Electricity and Magnetism, Vol 2", p. 24
"We call the statement in the box [Gauss's Law] because it is equivalent to Coulomb's [force] law and it could server equally well as the basic law of electrostatic interactions, after charges and fields have been defined. Gauss's law and Coulomb's law are not two independent physical laws, but the same law expressed in different ways."He does add a footnote that Gauss's law is more general that Coulomb's force law.
Here was my logic thinking that, in general, I must have a force equation where like charges attract. Coulomb's law says like electric forces repel. To be consistent with that, Gauss's law must also say that like electric forces repel. Newton's field equation is the opposite of Gauss's field equation, so like charges must attract. That must result in a force law where like charges attract.
That is not a circle of logic, it is a path, from Coulomb, to Gauss, to Newton, to a force law. I could say with utmost confidence that my field equations demand that like charges attract.
So where was my force equation?
I didn't have one.
Oh, I had tried a couple of times, but the calculation never worked out. I figured I was doing something wrong. It was one of the rare times when I made a file and put the calculation away. I knew I would have to do the direct calculation someday. I would revisit it from time to time, but when it flopped I just figured I was not bright enough to do it.
And getting the form of the equation is not enough. The same solution has to work between the force and the field equations. I was slow to pick up on that constraint. It is easier to treat them independently, which was my own fault.
In this derivation series, several people said the force equation, the one I had not figured out how to calculate, showed that like charges repelled. This is what drove me to pull out the folder and try again. Last weekend I was able to see what they said, that the standard derivation of the Lorentz force equation of EM always gave the Lorentz force equation of EM if one used the same current coupling term. Like charges repel for the Lorentz force equation.
The derivation was always ending up in the house of EM were like charges repel. The details that bothered me last weekend as it did in the past was I got all kinds of cross products. The entire thrust of the hypercomplex gravity proposal was symmetric cross products took the place of the standard cross product. That was not happening. Why?
Like the thorough experimenter I am, I decided to challenge an assumption I had made a few years ago, that the current coupling term for gravity should be a Lorentz invariant scalar. I erased the conjugate operator, repeated the calculation, and got my symmetric curls. The form was good. Too bad there was no way to find a solution that worked for both of them. A few more fair kicks to the groin by the critics, and I saw how to make the force equations and the field equations use the same solution. That is all I will present here, not the less than elegant process that got me this far.
Here is how I will proceed. I will derive the Lorentz force for EM nice and neat, so those folks who like the math can follow along. I will include the extension that gets to Coulomb's law. No matter which side of the fence you sit on in regards to my own work, that derivation will be a value or review. I will then repeat the calculation, side by side, so you can spot both Coulomb's law and the one Newton wrote down a good number of years ago. He did not derive the gravitational force this way, what with the calculus of variations a few years off into the future, relying instead on observational data.
The derive series was focused on fields. This is the modern way to do physics. I actually had some trouble switching back to Lagrangians for good old particles. That is what is needed to derive the Lorentz force. This is about pushing around a particle. There are two things one varies: position and velocity. I don't have the time/energy/stamina to do that, show this should look familiar to the standard Euler-Lagrange, but differing in some detail, like using the total time derivative (a critical detail by the way).
We start with a Lagrangian - no longer a density - that has a kinetic energy term and one for the current coupling and... nothing else. This is some serious minimalism. [Update: included the free field terms]
The V is the velocity. There is a real charge q instead of current densities. Here is the relevant equation:
This has a similar structure to the Euler-Lagrange equation used before because it is a non-relativistic variant. An important difference is that total time derivative.
Who changes with space (R)? The potentials phi and A. Who changes with respect to velocity (V)? The kinetic energy term and the current. Write that out:
Give the force an entire side:
Total time derivative sidebar: The total time derivative is made up of two parts. One is the partial derivative with respect to time, and the other has to do with moving changes in space. Recall the definition of the E field:
Notice the change in space has the same sign as the change in time. So the total time derivative of A can be viewed as this partial time derivative:
It takes a serious dose of work with vectors to prove that one, but please accept it for this blog. There is another bit of magic sauce/fancy vector identity I will use soon enough:
Ouch. I did check that one this weekend, takes about ten minutes, but not easy to summarize, sorry, other than the one that goes on the left is dotted twice.
Sidebar complete.
Plug in the partial derivatives for the total derivative of A:
That is the proof of the Lorentz force law, at least the non-relativistic form.
So that is enough, right? No. This was my own failure up to sometime late on Monday. One has to take the phi one found as a solution to the field equations, plug that equation in here, then show that the Lorentz force law indicates like charges repel (the force is positive).
The solution was Q/R, the derivative of that with respect to R is -Q/R2, so in the static case:
Good old Coulomb's law, first guessed by Joseph Priestly.
To do the hypercomplex gravity proposal, here is my Lagrangian [updated to include the free field terms]:
There is one vital difference when evaluating the total time derivative. The field used is small e:
Therefore changes in time have the opposite sign from changes in space for the hypercomplex gravity proposal.
Here is the side-by-side derivation of the Coulomb and Newtonian gravity equations via the hypercomplex Lagrangian:

The ink is drying on this one. Based on previous efforts, it should take about two weeks for me to come up with the Mathematica notebook.
[The image above was updated. Based on a discussion below, the initial version had a simpler proposal for the total derivative term, which unfortunately lead to terms that could not be express in terms of the fields e and b. Since the hypercomplex product has the symmetry of Z2xZ2, it may make sense to treat those terms with 2 spatial components as the space parts as was done in the above calculation.]
I wish to thank my critics who pushed me to make the solution to the field equations consistent with the force equations. The process is rarely pretty in any business, but I feel better about having a force equation after hoping it would appear for quite a few years.
Doug
Snarky puzzle. Show how to derive the Coulomb force equation if you start from Gauss's law. If you get stuck, read chapter 28-5 of David Halliday and Resnick, "Physics", part 2.
Google+ hangout: 11:00-11:45pm Eastern time, Tuesday-Friday. http://gplus.to/sweetser
This could be an efficient way to exchange a few ideas. If you have a question or two, hangout.
The tentative new t-shirt design, not yet for sale:
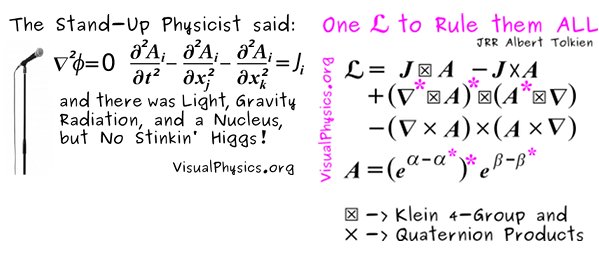
Next Monday/Tuesday: Gauge symmetries




Comments