Sixth Snarky Puzzle Answers

The sixth Snarky Puzzle Answers leads off with the story of a minor controversy.

[Click or skip this video reading on YouTube.]
Two related Snarky Puzzles
September 20, "Deriving the Maxwell Source Equations Using Quaternions (2/5)"

Snarky puzzle: This blog was too long. Make the author suffer. Let him figure out why B² - E² is invariant under a Lorentz boost.

October 4, "Deriving The Hypercomplex Gravity Field Equations (4/5)"

Snarky puzzle. Show that b² - e² is invariant under a Lorentz boost. I am pretty sure I did that calculation once.

Background
The short answer is that both B² - E² and E.B are invariant under a Lorentz boost. Despite how the question is phrased, the difference of the field b² - e² is not Lorentz invariant. The detailed calculations were done in a Mathematica notebook available here. Two commenters of the October 4 blog were able to spot the error in the question.

In my first job out of MIT, I was a lab tech. I didn't worry so much about the big picture, that is what the principle investigator did. What I focused on was thoroughly asking the question, making sure there were plenty of controls. It was fun to use that attitude to resolve this issue.

Experimental setup
There are two 4-vectors that get used in this analysis: a current density J and a potential A. The 4-derivative Del transforms like a dual 4-vector, the mirror image of how a 4-vector transforms.

There are three operations to do on these three:

Nothing
A 3D rotation around Z
A Lorentz boost along Z

Nothing is easy. Really, doing nothing for the first set is not a challenge.

The 3D rotation requires a little work that goes back to the 1850s. Quaternions remain a one-trick pony for doing the best 3D rotations in the business (fewer math operations, easier to correct for errors, and no gimbal lock). One needs a unitary quaternion. Let's use this one for a rotation around the Z axis:
$U = (cos(\alpha), 0, 0, sin(\alpha))$
The norm of this is unity because cosine square plus sine squared equals one. To do a rotation, escort any quaternion on either side by this unitary matrix and its conjugate:
$R \rightarrow R' &= U R U^*$

Do this little number on J, and one gets this rotated 4-vector:
$J \rightarrow J' = (\rho , Jx ~cos(2 \alpha ) - Jy~ sin(2 \alpha), Jy ~cos(2 \alpha ) + Jx ~sin(2 \alpha), Jz)$

The first and last terms are untouched, with the terms in the middle play trig games. Similar things can be done with the 4-vector A and the dual of Del. Those kinds of repetitive details are in the Mathematica notebook.

The way to do a Lorentz boost along Z using quaternions is not well known. As far as I can tell, such a trick is not in the literature. This means quaternions can be ignored by professionals for a valid reason: Lorentz boosts are too important.

All that is needed is a variation on the 3D rotation machine. Toss in hypercomplex functions instead of the regular trig functions:
$H = (cosh(\beta), 0, 0, sinh(\beta))$

This matrix is not unitary. Drop it into the same structure as a 3D rotation, and, oops, that does not work. Correct the flaws. Here is how to do a boost along the Z axis:
$B \rightarrow B' = H B H^* + ( (H H B)^* - (H^* H^* B)^* )/2$

As an example, boost the J vector along the Z axis:
$J \rightarrow J' = (\rho \cosh(2 \beta) - Jz \sinh(2 \beta), Jx , Jy , Jz \cosh(2 \beta ) - \rho \sinh(2 \beta))$

Similar boosts can be done for the potential A and dual of Del (in the notebook).

Three players - J, A, and Del - with three operations - nothing, a rotation, and a boost - make a set of nine possibilities.

There are two ways to form products: quaternion rules and those of the California representation of hypercomplex numbers, aka the Klein 4-group or quaternions without any minus signs.

These are the target products:
$\\ J \times A \\ J^* \boxtimes A \\ (Del \times A - (Del \times A)^*) \times (A \times Del - (A \times Del)^*) \\ (Del \times A - (Del \times A)^*)^2 - (A \times Del - (A \times Del)^*)^2 \\ (Del^* \boxtimes A - (Del^* \boxtimes A)^*)^* \boxtimes (A^* \boxtimes Del - (A^* \boxtimes Del)^*)$

If a product is invariant under a Lorentz transformation, then the first term of that product will be the same if one does nothing, a rotation or a boost.

There is a simple approach: do the rotations, the boosts, in different situations, and compare the results. There is a large volume of detail, all of which must be done perfectly. For $300, one can get Mathematica Home Edition for those outside of academia. Mathematica does not insure success as calculations can be set up incorrectly. The key to doing any experiment a good set of controls. I knew for example that the scalars of these must be exactly the same:
$\\ J \times A \\ JRotZ \times ARotZ \\ JBoostZ \times ABoostZ \\ J^* \boxtimes A \\ JRotZ^* \boxtimes ARotZ \\ JBoostZ^* \boxtimes ABoostZ$

That is a control for all the tools needed in this experimental setup: rotations, boosts, conjugates, quaternion and hypercomplex products. I also knew that these two must be invariant under the rotations and boosts:
$\\ (\nabla \times A - (\nabla \times A)^*) \times (A \times \nabla - (A \times \nabla)^*) \\ (\nabla \times A - (\nabla \times A)^*)^2 - (A \times \nabla - (A \times \nabla)^*)^2$

Answer
That left one experimental calculation:
$(Del^* \boxtimes A - (Del^* \boxtimes A)^*)^* \boxtimes (A^* \boxtimes Del - (A^* \boxtimes Del)^*)$

The first term for this product varied when rotated or boosted.

Discussion
The smarties in the class will say I wasted time proving what should be obvious. I prefer a thorough calculation since it can point out assumptions I may be making along the way.

Does this result mean the hypercomplex gravity field equation proposal took a bullet to the head? What other equations break global Lorentz symmetry?

General relativity
Loop quantum gravity (kinda the same thing)

Perfect, absolutely perfect. We might get into a bitter fight about global versus local symmetry breaking, but at least the hypercomplex gravity field equations are hanging around with the right kids in field theory.

September 13, "Deriving How To Derive Field Equations (1/5)"

Snarky puzzle

This one is lifted straight from the start of Chapter 19. Here is the path integral for a ball in a gravitational field.
$S =\int_{t_1}^{t_2} \left[ \frac{1}{2} m \left(\frac{d x}{d t} \right)^2 -m g x \right] dt.$
See if you can spot Newton's law of gravity here.

Answer
$m \frac{d^2 x}{d t^2} = -m g$

Discussion
What Feynman wondered about was how Nature did this kind of calculation on the fly. Answers to the simplest questions remain out of reach.

September 27, "Deriving the Maxwell Homogeneous Equations Using Quaternions (3/5)"

Snarky puzzle

Take one of the quaternion derivative ways to write the E and B fields and square it. Notice that the scalar is a Lagrange density that will be able to generate all four of the Maxwell equations via the Euler-Lagrange equation... [correction: NO, generates the homogeneous equations, not the source equations.]
Math overdose, scary-as-shit bonus problem: do something with the two 3-vectors generated [from the product that makes E.B].

Answer-free discussionAt 1am or so, I thought about
$scalar(0, -\vec{E} + \vec{B})^2 = -E^2+ 2 E \cdot B - B^2$

The Maxwell source equations need the difference of the two squares, but these have the same sign, so cannot be used to generate the Maxwell source equations, my bad.

I was able to do a bit of the math overdose problems since all the tools where there in a Mathematica notebook. These are the kinds of dense collections of partial differential equations one needs to look at over a long period of time to see if one can spot some sense in them. No can do tonight.

October 11, "Deriving The Unified GEM Field Equations (5/5)"

Snarky puzzle

I doubt it is meaningful, but do the sum of the gauge dependent Lagrange densities instead of the difference. Practice, practice, practice. Someday those equations might solve a deep mystery. Or not.

Background
I like to be complete. It struck me that working with only the difference of the gauge-dependent fields was not complete.

Answer
The Lagrange density has only the cross terms, which have contributions from each of the four positions in the 4-derivative or 4-potential. Once run through the Euler-Lagrange equation, one of the four symbols bows out, like so:
$\rho = \frac{\partial ^2 Ax}{\partial y\partial z}+\frac{\partial ^2 Ay}{\partial x\partial z}+\frac{\partial ^2Az}{\partial x\partial y} \\ Jx= \frac{\partial ^2Ay}{\partial t\partial z}+\frac{\partial ^2Az}{\partial t\partial y} -\frac{\partial ^2\phi }{\partial y\partial z} \\ Jy= \frac{\partial ^2Ax}{\partial t\partial z}+\frac{\partial ^2Az}{\partial t\partial x} -\frac{\partial ^2\phi }{\partial x\partial z} \\ Jz= \frac{\partial ^2Ax}{\partial t\partial y} +\frac{\partial ^2Ay}{\partial t\partial x} - \frac{\partial ^2\phi }{\partial x\partial y}$

Discussion
These field equations are mildly amusing. The first equation has rho, then dodges things like phi or time derivatives. A similar pattern holds for the rest. There is no reason to take this particular set of equations seriously at this time.

Doug

Google+ hangout: 11:00-11:45pm Eastern time, Tuesday-Friday. http://gplus.to/sweetser

This could be an efficient way to exchange a few ideas. If you have a question or two, hangout.

Bet against the Higgs being found, buy the t-shirt

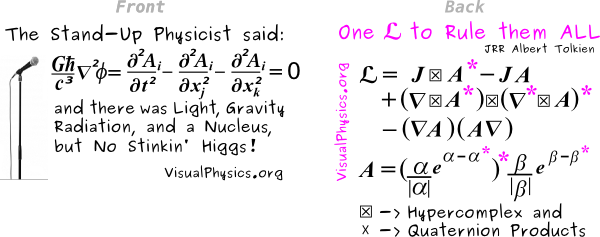
Next Monday/Tuesday: Gravity is a Mystery (in words, no equations)

Related articles

Comments

Know Science And Want To Write?

Donate or Buy SWAG