Velocipedological science
Cycling is more than just a pleasant way to keep fit: it is a pleasant way to learn some interesting velocipedological science facts. Don't just exercise your muscles: exercise your brain by cycling for science.
Scientists with too much time on their hands have spent more than a century trying to understand how bikes ride and steer and fail to fall down in the way they do.
Phil Daoust
The first and most important scientific fact about the bicycle is that you can never own enough bikes. This fact may be expressed as a formula:
Bi = Bc + 1
where, in most countries, Bi is the ideal number of bicycles to own and Bc is the current number of bicycles owned.
Although somewhat whimsical, Bi = Bc + 1 expresses two ideas:
1 - if you own zero bicycles you really should get one;
2 - there is no such thing as the ideal bicycle.
A bicycle ideally suited to climb hills is not ideally suited to race down them. A puddle-jumper or rock-hopper (trail or mountain bike) is not ideally suited for touring on tarmac roads. Whatever type of bike you own you will always find a purpose or terrain to which it is not suited: time to buy another bike!
Tensegrity
Buckminster Fuller coined the term tensegrity and developed many design ideas and concepts within that branch of engineering.
R. Buckminster Fuller was a 20th century inventor and visionary who did not limit himself to one field but worked as a 'comprehensive anticipatory design scientist' to solve global problems. Fuller's ideas and work continue to influence new generations of designers, architects, scientists and artists working to create a sustainable planet.Tensegrity structures are mechanically rigid structures based on components loaded in compression combined with components pre-loaded in tension. The most common tensegrity structure is the wire wheel as used worldwide for bicycles, motorbikes, carts etc.
The Buckminster Fuller Institute

Some of the author's wheels.
Photo credit Babatunde Olagunju
The radial spoke bicycle wheel, if one discounts the axle and bearings, is a pure tensegrity structure. It consists of a rim in compression joined to a hub maintained in radial tension by pre-tensioned spokes. The spokes being pre-tensioned place the hub in circumferential tension and the rim in circumferential compression. The flange on the hub which takes the spoke ends is subjected to forces which tend to "unzip" the flanges along the line of the holes.
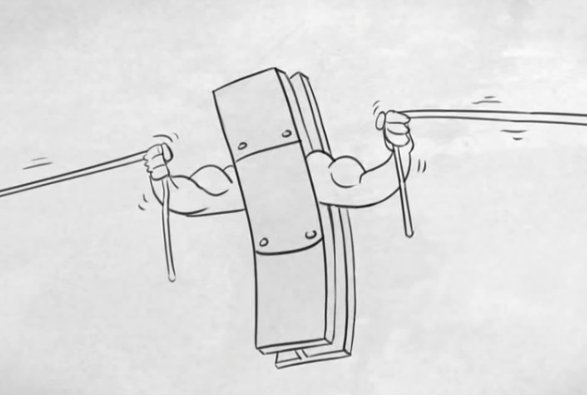
Screen shot from Ephemeralization - Doing more with less
(video below)
In the case of the tangentially spoked wheel the hub is subjected to tangential forces which are less likely to lead to hub breakage. However, the radial model of a rim in compression with spokes and hub pre-tensioned is still applicable to explanations of how the load of rider and bike frame is transmitted through the spokes to the rim, tire and ultimately the road.
Which spokes bear the load?
Some schools of thought would have the hub hang from the topmost spoke/s, others would have it stand on the bottom spoke/s. Both are wrong - or it might be said not even wrong. The greatest tension is experienced by those spokes which support the hub "tightrope fashion". In order to return the hub to the exact center of the wheel the spokes b and c in the diagram below would need to be tensioned to an infinite amount.
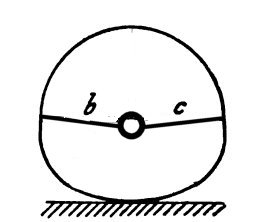
Spokes seen as a tightrope
Load transmission in a tension-spoke wheel.
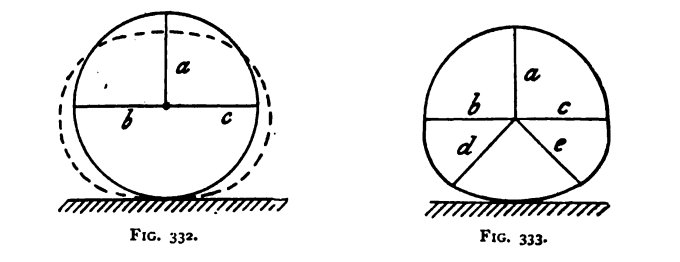
The method of action of the tension-spoke wheel may be shown as follows. Suppose the hub connected by a single wire, a, to a point on the top of the rim, a load applied at the centre of the wheel would be transferred to the top of the rim and would tend to flatten it, the sides would tend to bulge outwards, and the rim to assume the shape shown by the dotted lines (fig. 332). This horizontal bulging might be prevented by connecting the hub to the rim by two additional spokes, b and c. If, now, a load were applied at the centre of the wheel, the three spokes, a, b, and c, would be subjected to tension, and if the rim were not very stiff it would tend to flatten at its lower part, as indicated in figure 333. Additional spokes, d and e, would restrain this bulging. Thus, by using a sufficient number of spokes capable of resisting tension, the load applied at the centre of the wheel can be transmitted to the ground without appreciable distortion of the rim.
Bicycles&Tricycles, Archibald Sharp, 1896
Contrary to the opinions of many otherwise knowledgeable writers the weight of the rider and bicycle is never transmitted to the rim via compressive forces. Under normal conditions the load is transmitted from axle and hub via tensile forces to the rim and from the rim to the ground via compression. Imagine a wheel built using string in place of the spokes. You will see at once that no spoke transfers load in compression, simply because it is impossible to push a piece of string. Consider also that the spoke nipple is a free fit in the rim. If the hub could push a spoke it would simply cause the spoke nipple to protude - there would be no transfer of load from hub to rim whatsoever.
Compliance
Compliance, in simple terms, is the property of a first object pressed against a rigid second object or surface such that the first object complies with the resultant forces and assumes the shape of the contact area of the second object or surface.
The wire wheel, being a rigid tensegrity structure exhibits very low compliance in normal use.
The pneumatic tire with which most wire wheels are equipped acts in a combination of tension and compression to greatly increase the compliance of the wheel as a whole, thus relieving the metal parts (and the rider) of a great amount of impact loading.
The wire wheel, or more correctly the pre-tensioned-spoke wheel is much lighter than its forbears. In the field of velocipedology weight-saving is highly valued.
to be continued >>>
Related - and highly recommended - video
.



Comments