Spaces
Manifolds and Tangent Spaces
Einstein did something very different with his General Theory of Relativity. Something that had not been done in science anytime before that. He actually separated the space "where we put a box"—the space of "places" or locations—from the space of "directions" or vectors (velocity, acceleration, momentum, electric and magnetic fields, etc.).1
The space of locations is called a manifold. This is probably an unfamiliar term for many (except that those familiar with automobile engines know about intake and exhaust manifolds). You can just think about a manifold as being the set of all possible locations, possibly on some high dimensional curved "surface".2
When viewed very close to a single location—a single point—a smooth manifold will look like a flat space—a vector space. The tangent space is the vector space that is tangent to the smooth manifold at a single point—the one that looks the most like the smooth manifold at that point, when viewed very closely.
We are all familiar with a curved manifold, and the tangent spaces to that manifold: The surface of the Earth (whether considered to be a smooth sphere, or as a sufficiently smoothed version of the actual location complete with hills, mountains, and valleys) is a two dimensional manifold. The tangent space to that manifold, at any given point on that manifold, is a mathematical (Euclidean) plane, which we can imagine—or, in some cases, partially
construct—at any given point on the Earth's surface. Some ways in which we may partially construct or realize a tangent space at a point on the surface of the Earth is when we level a portion of the ground for the foundation of a building, or lay a board or sheet of glass on the ground.
So, from here on, we shall be only considering the tangent space—the vector space. So we will no longer have to consider the collection of locations that is the manifold, even if it is flat.3
Vector Spaces
OK. Now that we are focusing on the tangent space—a vector space—what is a vector space?
Mathematicians define a vector space in the following manner (underlined words/phrases are terms that are being defined):
Let F be a (mathematical) field (like the Real or Complex numbers). A vector space over F (or F-vector space) consists of an abelian group4 (meaning the elements of the group all commute) V under addition together with an operation of scalar multiplication of each element of V by each element of F on the left, such that for all a,b ∈ F (read a,b in F, or a,b elements of F) and α,β ∈ V the following conditions are satisfied: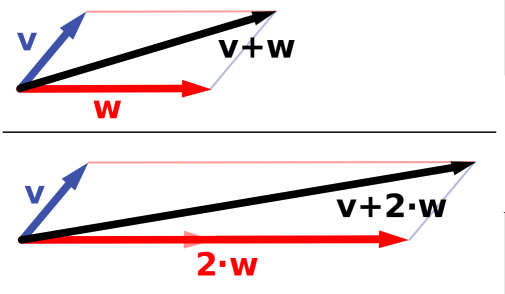
V1) aα ∈ V.
V2) a(bα) = (ab)α.
V3) (a+b)α = (aα) + (bα).
V4) a(α+β) = (aα) + (aβ).
V5) 1α = α.
The elements of V are called vectors, and the elements of F are called scalars.
Well, some of you have probably seen a definition like this before. Some of you may not recall ever having seen a definition like this before, but are OK with this definition. Others are scratching their heads and wondering whether they are going to be able to follow this series at all, if we're going to be having stuff like this!
 The important takeaway message is that a vector space contains things we call vectors, that have some "amount" in some "direction" (hence the reason we tend to depict them using arrows of various lengths pointing off in different directions). These vectors can be added together, without having to worry about what order we add them (just like with ordinary numbers), to produce new vectors. We can multiply these vectors by scalars—numbers like Real or Complex numbers—to also produce new vectors. And the operations of adding vectors and multiplying by scalars can be combined in what would seem to be the "usual way" from our experiences with plain old ordinary numbers (Counting Numbers, Integers, Real and Complex numbers), via the operations shown in V2 through V5. Other than that, the definitions simply make sure everyone is working with these things in exactly the same way, to avoid misunderstandings.
The important takeaway message is that a vector space contains things we call vectors, that have some "amount" in some "direction" (hence the reason we tend to depict them using arrows of various lengths pointing off in different directions). These vectors can be added together, without having to worry about what order we add them (just like with ordinary numbers), to produce new vectors. We can multiply these vectors by scalars—numbers like Real or Complex numbers—to also produce new vectors. And the operations of adding vectors and multiplying by scalars can be combined in what would seem to be the "usual way" from our experiences with plain old ordinary numbers (Counting Numbers, Integers, Real and Complex numbers), via the operations shown in V2 through V5. Other than that, the definitions simply make sure everyone is working with these things in exactly the same way, to avoid misunderstandings.
Remind me, why are we concerned about "vector spaces"? Because, like the picture to the right, we use directions and "amounts" of things (like distance, speed, acceleration, electric and magnetic field, etc.) both in everyday life, and especially in physics. Such seem to be reasonably natural, quite expressive, and useful.
Now that we have vectors, and vector spaces, we've got everything we need, right? No. Not quite. Some readers may have notices that I kept referring to nebulous things like "amount" and direction when talking about vectors. Shouldn't I have been talking about magnitude and direction? After all, that's how most have heard of such things when talking about vectors.
The problem is that, at this point, we don't have any real way to determine magnitude, and even direction—especially of one vector relative to another—is not well defined.
Not well defined?!? I hear some shouting. What's not well defined about such things? You simply...
Inner or Dot Products
OK. Let's take care of this magnitude and direction issue...
By a show of hands, who has heard of an inner or dot product of vectors? I suspect that practically everyone here that has heard of vectors, before this article, has also learned about the dot or inner product of vectors, and how this relates to magnitudes and directions of vectors.
However, how many of you know that just because you have a vector space does not guarantee that you have a dot or inner product? You see, just because you have vectors, in a vector space, does not, necessarily, mean that you also have the ability to take dot/inner products of such vectors! The ability is an additional feature in addition to the structure of a vector space.
All right, so what's so mysterious about having a dot or inner product? Well, the real question is what is the inner or dot product?
Remember, the vector space has vectors, and these numbers called scalars. In the case of the "real world" the only numbers we truly have to deal with are (drum roll, please ...) the Real numbers.5 ;) So, from here on, we shall focus only on vector spaces over the Real numbers, or Real vector spaces.6 Therefore, the scalars we will be dealing with will be Real numbers.
The thing to recognize is that the dot or inner product is another binary operation (· or <,> or <|>), or function, g, that takes two vectors, from the vector space, and yields a scalar from the number field associated with the vector space (the Real numbers, in our case). So for all α,β,γ ∈ V, α·β = <α,β> = <α|β> = g(α,β) ∈ F (which is the Real numbers, in our case), and satisfies the following (we will simply use the dot notation, α·β):
D1) α·β = β·α (conjugate symmetry becomes simple symmetry for Real numbers)
D2) (aα)·β = a(α·β) and (α+β)·γ = α·γ+β·γ (linearity in the first argument)
D3) α·α ≥ 0 with equality only for α = 0 (positive-definiteness)
This can all be succinctly summarized (for those that are comfortable with the terms) by stating that the dot/inner product is a positive-definite Symmetric bilinear (Hermitian) form.
So, an inner product space is a vector space with the addition of this inner product operation or function. If we don't have this additional operation or function, we cannot determine the magnitudes of vectors, nor the relative directions, or angles between vectors. Similarly, if we are able to determine magnitudes (lengths, etc.) of vectors, and angles (relative directions) between vectors, in a consistent manner, then we have, or can construct this very operation or function.
The truth is, we now have, with this inner or dot product, the METRIC (hear sound of this shout, in a deep bass voice, reverberating off the mountainsides...). We simply need to take a closer look, expanding the vector space in terms of a basis (as we always can do for a vector space), and, ultimately, relaxing condition D3, the positive-definiteness condition.
That's what we will be addressing next time.
1 Bernhard Riemann, a mathematician, created the geometry that caries his name in the nineteenth century in order to handle the geometry of curved surfaces without having to consider how such surfaces may be embedded in some higher dimensional space.
2 The inner or outer surfaces of intake and exhaust manifolds can be considered as examples of two dimensional manifolds, in this sense.
3 A flat manifold can be identified with its tangent spaces: All the tangent spaces can be identified with one-another (made "the same"), and the flat manifold can then be considered to be "identical" to this tangent space. This is what "allows" the usual physics where vectors, such as velocity, etc., can "appear" on the same space as displacement vectors (straight line movement from one location/point to another), and actual locations/points (and collections of such, like boxes and other objects).
4 An abelian group (over addition) is a group where all elements commute: So, for a,b ∈ A (read a,b in A, or a,b elements of A), a+b = b+a. Mathematicians define a group in the following manner:
A group <G, *> is a set G, together with a binary operation * on G, such that the following axioms are satisfied:
G1) The binary operation is associative: (a*b)*c = a*(b*c).
G2) There is an element e in G such that e*x = x*e = x for all x ∈ G. (This element e is an identity element for * on G.)
G3) For each a in G, there is an element a' in G with the property that a'*a = a*a' = e. (The element a' is an inverse of a with respect to *.)
Some will note that this list of axioms is missing "closure". Very good! This is because the text that I have used defines a "binary operation" in the following manner:
A binary operation * on a set is a rule that assigns to each ordered pair of elements of the set some element of the set. So, in this case, the definition of a binary operation * on a set already includes the concept that the set is closed under the operation *.
5 I know that Quantum Mechanics "needs" the Complex numbers. However, even then, the only numbers we humans ever see from a Quantum Mechanical experiment are, again, always Real numbers. Besides, we are dealing with classical level "things" (like velocities, accelerations, electric and magnetic fields, etc.) for the sake of this series.
6 It's actually not difficult to generalize an inner product space to being over the Complex numbers. It's just that it will help (I believe) if we are a little bit more focused, here.
Articles in this series:
What is the Geometry of Spacetime? — Introduction (previous article)
What is the Geometry of Spacetime? — What is Space? — Inner-Product Spaces (this article)
What Is The Geometry Of Spacetime? — What Kinds Of Inner-Products/Metrics? (next article)



Comments