It is the issues/questions of the metric, its relationship to the inner or dot product, and what forms it may take that we shall address in this installment. As for how the possible forms of the metric relate to the usual "strangeness" of the Special Theory of Relativity, we may be able to address such within the comments section. If not, we'll have a fourth installment.
We Have the Metric, You Say
 OK. You will recall that we defined the inner or dot product, on our vector space(s) (the tangent space[s]), thus giving us an inner product space(s).2 So, the question, now, is how does the inner or dot product relate to what is called the metric, or the metric matrix (or tensor).
OK. You will recall that we defined the inner or dot product, on our vector space(s) (the tangent space[s]), thus giving us an inner product space(s).2 So, the question, now, is how does the inner or dot product relate to what is called the metric, or the metric matrix (or tensor).
Recall that from the definition of the inner or dot product we may take any two vectors, such as x,y ∈ V (our vector space), and obtain a scalar (from the associated mathematical field, F, to our vector space) by way of the operation x·y = y·x = g(x,y) ∈ F (which is the Real numbers, in our case).
OK. Fair enough, but how do we "find" these scalars? Can we simply pick them "out of a hat", so to speak, or is there some more specific procedure?
Recall, again, that we are dealing with a vector space, V (our vector space), and vector spaces have certain features and characteristics.3 So, we can use these features to always set up a "basis" for our vector space.
A Basis for Our Vector Space, and Expanding the Inner Product
 I will not go into the proof here, but suffice it to say that for any finite dimensional vector space, of dimension n, we can obtain n linearly independent vectors, called basis vectors, such that any and all elements of our vector space can be written as a linear combination of these basis vectors. That is, we can obtain a set of n linearly independent basis vectors, β1,β2,…,βn ∈ V (our vector space), such that for any and all x ∈ V, we can find (unique) scalars, a1,a2,…,an ∈ F (the Real numbers, in our case), so x = a1β1 + a2β2 +…+ anβn = Σi=1n aiβi.
I will not go into the proof here, but suffice it to say that for any finite dimensional vector space, of dimension n, we can obtain n linearly independent vectors, called basis vectors, such that any and all elements of our vector space can be written as a linear combination of these basis vectors. That is, we can obtain a set of n linearly independent basis vectors, β1,β2,…,βn ∈ V (our vector space), such that for any and all x ∈ V, we can find (unique) scalars, a1,a2,…,an ∈ F (the Real numbers, in our case), so x = a1β1 + a2β2 +…+ anβn = Σi=1n aiβi.
Therefore, for all x,y ∈ V (our vector space), we can expand the inner or dot product using the chosen basis (so x = Σi=1n aiβi, and y = Σi=1n biβi) in the following manner: x·y = y·x = g(x,y) = Σi=1n ai g(βi,y) = Σi=1n ai g(y,βi) = Σi=1n Σj=1n ai bj g(βj,βi) = Σi=1n Σj=1n ai bj g(βi,βj). Since for any choice of basis vectors, β1,β2,…,βn ∈ V, the inner or dot product of any two vectors will always be given in terms of the symmetric set of scalars, g(βi,βj) ∈ F, we may simply codify these scalars as a symmetric matrix gij = g(βi,βj) = βi·βj (a Real Gramian [or Gram] matrix).
This should be recognizable as the usual, symmetric matrix (or tensor) representation of the metric. All it took was expanding the inner or dot product in some (any) chosen basis for the vector space.
Other Restrictions on the Inner or Dot Product?
OK. The inner or dot product can be characterized by a symmetric matrix (or tensor) of scalars (from the Real numbers, in our case), but is that it? Are there no other restrictions?
The more observant readers will have noticed that only the first two conditions placed upon an inner or dot product by its definition were used in the expansion, above (namely symmetry, and linearity in the first argument). However, there is a third condition placed upon inner or dot products, namely positive-definiteness.
Since the condition of positive-definiteness is expressed in terms of the inner or dot product of any and all vectors with themselves, we need to expand this requirement in terms of the chosen basis, as well. Recall that the condition states that for all x ∈ V, x·x ≥ 0 with equality only for x = 0.
Using the expansion in terms of the chosen basis, namely x = Σi=1n aiβi, we first see that x = 0 implied that all the coefficients ai = 0 (since the basis vectors β1,β2,…,βn ∈ V are required to be linearly independent). However, expanding the first part of the condition yields: 0 ≤ x·x = Σi=1n Σj=1n ai aj gij, for all a1,a2,…,an ∈ F (the Real numbers, in our case), with equality only for all the coefficients ai = 0.
So, the positive-definiteness requirement on an inner or dot product translates directly to a similar requirement upon the metric matrix (or tensor). We say that the symmetric matrix, gij, is required to be positive-definite (where that is defined by the condition, above).
What Kinds of Symmetric Matrices are Possible?
Now that we have the inner or dot product expressed in terms of a symmetric matrix (or tensor), it can be quite useful to ask: What kinds of symmetric matrices are possible? Are they all different, or are there similarities? Can they be classified/categorized?
Remember that our choice of basis vectors, for our vector space V, is quite arbitrary. The one and only condition/requirement is that the basis vectors must be linearly independent (meaning that 0 = Σi=1n aiβi if and only if all the coefficients ai = 0). So we may choose any other set of basis vectors, such as β'1,β'2,…,β'n ∈ V, to investigate the relationships between two sets of basis vectors.
One Basis in Terms of Another
Since all vectors within the vector space may be written as linear combinations of any set of basis vectors, we may certainly write any set of basis vectors in terms of another set. For instance, for all i ∈ {1,2,…,n}, β'i = Σj=1n Λij βj, and, similarly, βi = Σj=1n Λ'ij β'j., where the Λ and Λ' matrices represent their respective change of basis transformations.
Applying these transformations in a cycle (from the un-primed to the primed, and back again), we see that for all i ∈ {1,2,…,n}, βi = Σj=1n Λ'ij β'j = Σj=1n Λ'ij Σk=1n Λjk βk = Σk=1n (Σj=1n Λ'ij Λjk) βk. Therefore, since the basis vectors are linearly independent, we must have Σj=1n Λ'ij Λjk = δik (the identity matrix, with ones [1] along the major diagonal [i=j], and zeros [0] everywhere else). So Λ and Λ' are (matrix) inverses of one another. Therefore, the change of basis vectors, between any two sets of basis vectors, may be related by an arbitrary, invertible linear transformation.4
How do the Metrics Relate?
Now that we know how one set of basis vectors relates to another, how will the metric in one basis relate to that within another basis? Remember that the metric is really just the inner or dot product expressed within some chosen set of basis vectors. So, regardless of the chosen set of basis vectors, they are still expressing the same inner or dot product.
Expressing the same inner or dot product in two different sets of basis vector yields: gij = g(βi,βj) = g(Σk=1n Λ'ik β'k, Σl=1n Λ'jl β'l) = Σk=1n Λ'ik Σl=1n Λ'jl g(β'k,β'l) = Σk=1n Σl=1n Λ'ik Λ'jl g'kl. So, the metrics are directly related by the matrix congruence (transformation). Expressed as matrices, we have g = Λ' g' Λ'T (where the superscript T stands for the matrix transpose).
So, What are the Categories of Symmetric Matrices
So, now that we know how these symmetric matrices, that encode the metric, transform between choices in the set of basis vectors for our vector space, we can finally answer the question of what are the different categories. In other words, what sets of symmetric matrices do not transform into one another by way of this matrix congruence (transformation)?
Proposition: If two symmetric matrices are related by a matrix congruence (transformation), then we shall consider them to be in the same category. Corollary: All matrices related to one another, or, equivalently, to some representative matrix, by matrix congruences (or congruence transformations), are in the same category. So, if we can determine the complete set of such representative matrices for all such categories, then we will have a complete accounting of all such categories.
As it so happens, Real symmetric matrices (as we have) have a special quality: They can all be diagonalized by orthogonal transformations. So, for any Real symmetric matrix, g, there exist orthogonal transformations (O, for instance, so OT = O-1 [the matrix inverse of O]), such that OT g O = λ, a diagonal matrix (so the only non-zero values are on the major diagonal of the matrix).5 In fact, since changing the order of the elements along the diagonal of a diagonal matrix requires only another orthogonal transformation, and since the product of orthogonal matrices is also orthogonal, we can always arrange the order of the elements along the diagonal of λ to be any order we may desire.6
Now, in our case, we have all invertible, Real transformations at our disposal, not just orthogonal transformations, but they include all orthogonal transformations as well. So, not only can we diagonalize all of the symmetric real matrices we may encode (as metrics), we can actually change the values of the diagonal elements. At least, up to a point.
For instance, if we follow the orthogonal matrix that diagonalizes our symmetric matrix, g, by a diagonal matrix, d, we can rescale the diagonal matrix so produced (let M = d OT): M g MT = d OT g O d = d λ d, which is also diagonal. In fact, if we choose the elements along the diagonal matrix d to be just right (though the signs don't make any difference), the reader will notice that we may always "normalize" this diagonal matrix, d λ d, to have only elements in the set {-1, 0, +1} along its diagonal (and we may always group them in any order we may choose, since that can be accomplished as a part of the orthogonal transformation O).
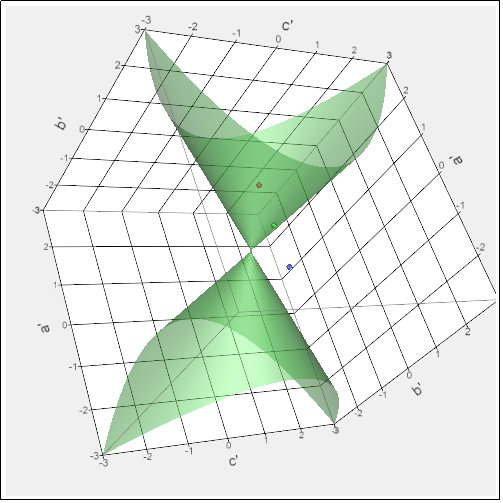 So, as candidates for the representative matrices for all of the categories of symmetric matrices (encoding our metric), we have diagonal matrices with n- -1 elements, n0 0 elements, and n+ +1 elements, such that n- + n0 + n+ = n (the dimensionality of our vector space, of course). Since all symmetric matrices are related to these matrices by matrix congruences (or congruence transformations) there are no other categories. All that remains is to prove that there are no fewer categories (we can call them congruence classes), by proving that none of these representative matrices are related to any other representative matrices by any matrix congruences (or congruence transformations). (This will be an assignment for the reader, if any so choose, but remember that the transformation matrices must be invertible [non-singular]. You may want to check into Sylvester's law of inertia.)
So, as candidates for the representative matrices for all of the categories of symmetric matrices (encoding our metric), we have diagonal matrices with n- -1 elements, n0 0 elements, and n+ +1 elements, such that n- + n0 + n+ = n (the dimensionality of our vector space, of course). Since all symmetric matrices are related to these matrices by matrix congruences (or congruence transformations) there are no other categories. All that remains is to prove that there are no fewer categories (we can call them congruence classes), by proving that none of these representative matrices are related to any other representative matrices by any matrix congruences (or congruence transformations). (This will be an assignment for the reader, if any so choose, but remember that the transformation matrices must be invertible [non-singular]. You may want to check into Sylvester's law of inertia.)
But we were Talking About Metrics
OK. So we now have a categorization of symmetric matrices that transform via matrix congruences (or congruence transformations). However, as noted under the heading "Other Restrictions on the Inner or Dot Product?", above, the positive-definite requirement on the inner or dot product restricts the metric matrix (or tensor) to also be positive-definite. So, which of the congruence classes are positive-definite?
Recall that the positive-definite restriction is expressible as: 0 ≤ x·x = Σi=1n Σj=1n ai aj gij, for all a1,a2,…,an ∈ F (the Real numbers, in our case), with equality only for all the coefficients ai = 0. We can recast this in matrix notation as 0 ≤ x g xT, for all x = (a1,a2,…,an) (a row vector), with equality only for x = 0 = (0,0,…,0) (a row vector of all zeros).
Recall that there exists an invertible transformation, M, such that M g MT is a diagonal matrix, d, with only elements from the set {-1, 0, +1} along the diagonal. So we may rewrite the positive-definite requirement once again as 0 ≤ x g xT = x M-1 M g MT (M-1)T xT = (x M-1) d (x M-1)T = x' d x'T, for all x', with equality only for x' = 0.
It is easy to recognize that if there are any diagonal elements of d that are zero or negative (-1), this condition will be violated. So, the only congruence class that is positive-definite is the class congruent with the identity matrix (n- = 0 = n0, and n+ = n). This eliminates a great many possibilities. Even for two (2) dimensions we are eliminating the negative of the identity (the negative-definite case, which is, as far as science can determine, physically indistinguishable from the positive-definite case), the Special Relativistic like case with one +1 and one -1 on the diagonal (1+1 spacetime), along with the Newtonian/Galilean like case with one zero (0) and one +1 on the diagonal, and the negative of that (not to mention the trivial zero matrix).
Furthermore, what makes anyone think that Nature (not the rag) would be bound by such an arbitrary restriction. Wouldn't it make far more sense to determine the congruence class of the physical metric—the one that is actually used by, or stems from Nature (not the rag)—from experimental evidence, rather than simply as some einsatz7 imposed by Mathematicians based upon little real-world experience?
Please let me know what you think, in the comments section.
1 I'm ever so sorry it has taken me so long to get this installment of this series out to you all. Life and work have simply been far too much for me, the last six months or so. Thank goodness for the Thanksgiving Holidays! :)
2 The thing to recognize is that the dot or inner product is another binary operation (· or <,> or <|>), or function, g, that takes two vectors, from the vector space, and yields a scalar from the number field associated with the vector space (the Real numbers, in our case). So for all x,y,z ∈ V, x·y = <x,y> = <x|y> = g(x,y) ∈ F (which is the Real numbers, in our case), and satisfies the following (we will simply use the dot notation, x·y):
D1) x·y = y·x (conjugate symmetry becomes simple symmetry for Real numbers)
D2) (ax)·y = a(x·y) and (x+y)·z = x·z+y·z (linearity in the first argument)
D3) x·x ≥ 0 with equality only for x = 0 (positive-definiteness)
This can all be succinctly summarized (for those that are comfortable with the terms) by stating that the dot/inner product is a positive-definite Symmetric bilinear (Hermitian) form.
3 Mathematicians define a vector space in the following manner:
Let F be a (mathematical) field (like the Real or Complex numbers). A vector space over F (or F-vector space) consists of an abelian group (meaning the elements of the group all commute) V under addition together with an operation of scalar multiplication of each element of V by each element of F on the left, such that for all a,b ∈ F and v,w ∈ V the following conditions are satisfied:
V1) av ∈ V.
V2) a(bv) = (ab)v.
V3) (a+b)v = (av) + (bv).
V4) a(v+w) = (av) + (aw).
V5) 1v = v.
The elements of V are called vectors, and the elements of F are called scalars.
4 Of course they must be invertible (non-singular) for how else could both sets of basis vectors be linearly independent sets (within each set, of course, since there is no requirement that one set of basis vectors be in any way independent from any other).
5 The reader will notice that the diagonalization of a symmetric matrix, by way of an orthogonal matrix, is also a matrix congruence (transformation).
6 This is all highly related to eigenvalues, eigenvectors, and eigendecomposition. We run into such things over and over again within Physics, though, sometimes, such involve vector spaces that are not finite in dimensionality.
7 I'm not absolutely certain that this is the correct German word, or the proper form. It is simply the closest I have found to the one I have heard and used verbally.
Articles in this series:
What is the Geometry of Spacetime? — Introduction (first article)
What is the Geometry of Spacetime? — What is Space? — Inner-Product Spaces (previous article)
What is the Geometry of Spacetime? — What Kinds of Inner-Products/Metrics? (this article)




Comments