In the Standard Model, the theory of fundamental interactions among elementary particles which enshrines our current understanding of the subnuclear world, particles that constitute matter are fermionic: they have a haif-integer value of a quantity we call spin; and particles that mediate interactions between those fermions, keeping them together and governing their behaviour, are bosonic: they have an integer value of spin.
The distinction between half-integer and integer values of spin has such an enormous impact on the phenomenology of fundamental physics that its extent always surprises me. Of course, the magic comes through the fact that these particles obey the rules of quantum mechanics. In particular, one rule (a by-product of conservation of angular momentum) demands that all reactions among particles involve only integer changes of the total spin of initial and final state. [Initial and final state denote the system before and after the reaction has taken place, in case you wondered].
The reason of the above rule is that there has to be a conservation of the total angular momentum of the system, whatever reaction takes place. Spin and orbital angular momentum contribute to the total angular momentum of a system. We can absorb integer changes of total spin by allowing for variations of the orbital angular momentum of the involved particles, but half-integer changes are unaccountable - so they simply do not take place.
Putting the rule to work
To see how profoundly this simple rule affects the phenomenology of particle reactions, let us first take a fermion f of spin 1/2. Can we imagine a reaction whereby f emits a copy of itself, effectively cloning itself - f --> ff ? The above rule forbids it, as there would be a spin of 1/2 in the initial state of the reaction, and a total spin of 0 or 1 (depending whether the final spins of the two outgoing f particles are aligned or anti-aligned along some pre-defined quantization axis) in the final state.
So fermions are disallowed to reproduce by parthenogenesis!
Now imagine you are a boson g of spin 1, say. If we do not specify anything else about you, quantum mechanics instead allows you to split into a pair gg of identical bosons of spin 1. The initial value of spin is 1, the final value of spin is zero or two, and you are good. The above is exactly what happens to gluons. Gluons can self-interact, such that the reaction g-->gg is allowed. And whatever is allowed, in quantum mechanics, forcefully happens.
Note that gluon self-interaction is possible because QCD, the theory of the strong interactions that have gluons as mediators, has a mathematical description that allows it; without that, gluon would not be prevented to undergo g-->gg splitting by the integer spin change rule stated above, but they would still not do it (in other words, a "more fundamental" disallowance would exist in the absence of the interaction responsible for the splitting). We have a very clear example of that if we consider the photon: the photon also has spin 1, but the reaction γ --> γγ does not take place because the underlying maths of Electromagnetic (EM) interactions does not have the required flexibility (in Physics lingo, EM theory is Abelian, QCD is non-Abelian).
And What About the Higgs Boson?
Does the gluon-spewing trick discussed above also apply to Higgs bosons? The Higgs has spin 0, so certainly h --> hh does not violate the spin rule: 0+0 is always 0. Does it mean it happens? Well, as before, it depends on whether the mathematical description of the Higgs boson has the necessary flexibility to allow for it. Now, that is surprisingly still an open question, one which the LHC is burning a lot of rubber to address (see the promising graph of acquired luminosity in this year's run below).

(Above, the integrated luminosity of 2018 until July 5th is the darkest curve on the left, which shows a very high-slope trend during the non-shutdown times until mid June).
The task is complex, as we need to experimentally observe the production of a pair of Higgs bosons in the same collision - a rare occurrence!, and ascertain that the two bosons were produced by the splitting of a single Higgs, rather than emitted by initial-state particles in different space-time points. In fact, the simplest processes that lead to two Higgs bosons in proton-proton collisions include one which has a h-->hh splitting (the one on the right below), but also one which does not require the self-interaction process (the one on the left). In the diagrams, time flows from left to right. Gluons collide, create a loop of heavy quarks, and the heavy quark line produces either two Higgs bosons at separate points (left), or a single Higgs (right), which later splits into two.
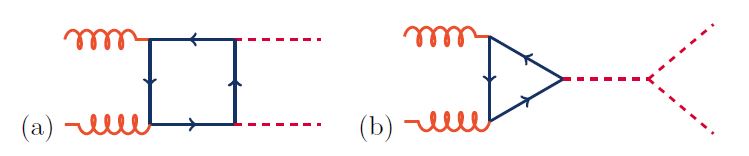
In-the-know readers could object that the Higgs boson is quite different from gluons and photons, as at variance with them it possesses a hefty 125 GeV mass. How can a 125 GeV object create two 125 GeV objects? This would violate a much more fundamental law, the one of conservation of energy! Well, that's true in principle, but quantum mechanics allows particles to waive that rule for brief instants of time. In other words, the energy conservation police will not consider it a violation if some imbalance is created for a really short instant.
More to the point for the present case, you should note that when we speak of the "mass" of a particle, we mean a number which characterizes the mean of a distribution, which has a characteristic shape (Breit-Wigner, or Lorentzian) whose width depends on the particle lifetime. So speaking of a Higgs boson produced with a mass of 250 GeV is not anathema. Two protons may collide, create a Higgs boson with a high "virtuality" (i.e., one which is highly off its nominal mass value, so "off-mass-shell"), and the latter can decay to two "on-shell" Higgs bosons.
I would like you to appreciate why the LHC is after this Higgs-pair-production process: it gives us access to a precise knowledge of the mathematical structure of the part of the theory dealing with the Higgs, the so-called Higgs Lagrangian. In general that all-important formula might include a term allowing for Higgs self-interaction, which we could write down simply as λh^3, with h the Higgs field and λ a real number. The existence of such a term would permit h-->hh reactions, like a similar term in the QCD Lagrangian does to gluons.
The goal is then to measure the λ parameter. If we find it equal to the SM prediction we can pat our backs and go home half-happy and half-sad. If we instead find it smaller or larger, we have new physics!
LHC: The Challenge Is On
The challenge is on, and ATLAS and CMS are devoting a lot of effort in searches for Higgs boson pairs in their datasets. There are heaps of ways to produce a pair of Higgs bosons in a proton-proton collision, and all of them must be exploited; their distinctive characteristics are invaluable to distinguish the signal from all backgrounds, so targeted searches are required. But also, the Higgs boson has this fantastic property of being able to decay into many different final states. Because of that, there are a lot of different possible ways to search for the process.
Say you produced two higgs bosons, in a proton-proton collisions. Now each Higgs decays, with the following rough probability shares:
b-quark pairs, 58%You are invited to mix and match the above final states of each Higgs decay, producing estimates of the fraction of Higgs pairs that end up in four b-quark jets (0.58*0.58 = 33%) or other combinations. Since the process is **very** rare to begin with, you realize soon that you can hardly afford to consider combinations where neither Higgs goes to a b-quark pair or a W boson pair.
c-quark pairs, 3%
tau-lepton pairs, 6.3%
muon pairs, 0.02%
gluon pairs, 8%
photon pairs, 0.2%
W boson pairs, 21.3%
Z boson pairs, 2.8%
Let me make a worked out example to clarify this. Suppose you take all the proton-proton collision data acquired by either CMS or ATLAS until now in 13 TeV energy running. This is something of the order of 100 inverse femtobarns of data. The predicted cross section of Higgs pair production is 40 femtobarns, so in those data you expect to have a chance to spot 40 fb * 100/fb = 4000 events of signal. Simple, ain't it? We just multiplied luminosity by cross section and got the number of produced collisions of that kind.
Now, say we want to spot events of the kind hh --> ZZ tau tau, for no other reason than sake of argument. We expect to have 4000 * 0.028 * 0.063 of them = 7 events ! That is quite small a number, as you must then consider that the typical efficiency of detecting Z bosons and tau leptons in either CMS or ATLAS is only of a few percent itself...
hh --> bbbb: The New CMS Result
So let us go for the hh-->bbbb reaction instead. Of course, that is the most frequent possibility - we expect to have about 1300 of these events in our data. The problem with the four b-quarks is that they are produced also by a nasty forest of QCD reactions, that collectively have a cross section of *many* orders of magnitude larger than the signal.
CMS just published a result of the search of 4 b-quark events in data they collected in 2016 - so 36/fb in total. In their analysis the name of the game was not just "beat the background" - by itself a very hard challenge, as after a selection of 4-b-jets-looking events they remained with over 180,000, with only a handful of signal events expected to have survived in that selected sample. Given the smallness of the signal in absolute terms, the crucial part of the study was in fact that of correctly estimating the background rate.
We used a very performant Boosted Decision Tree discriminant, tuned to best distinguish the hh decay from all QCD-induced events, and a multivariate technique called "Hemisphere Mixing" to generate artificial events to model the QCD background, which was otherwise difficult to simulate with computer programs. I have described the Hemisphere Mixing technique, which is a product of my research group, in a publication here (arxiv:1712.02538).
The distribution of the BDT classifier output has a high peak at low values (very QCD-like) and a very faint tail at the highest values, where the signal is comparatively more pronounced. Therefore, by precisely knowing these two shapes, one can fit them to best match the distribution observed in real data. The BDT output is shown in the graph below for data collected in a "control region" devoid of signal by kinematical cuts. The comparison of the data (black points) with the model (histogram, labeled "mixed data") in the left graph allows to evidence a oh-so-small but still significant bias in the prediction.
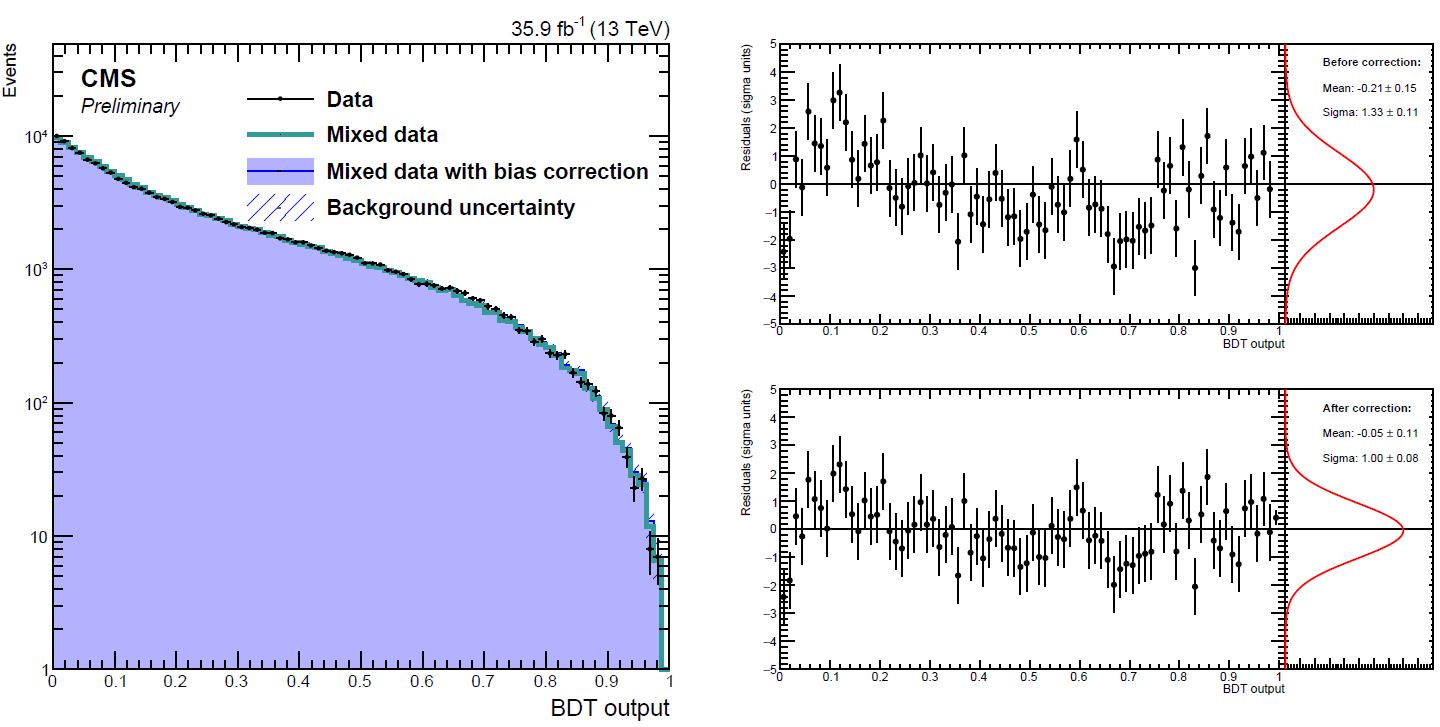
The graph on the top right shows the difference between data and model as a function of BDT output: a trend in the residuals is visible, and also evidenced by the wider-than-expected Gaussian profile of differences divided by uncertainty (top right). Once the bias is corrected, by a very complex resampling procedure, the agreement improves significantly (bottom left, the residuals after the correction).
A large number of additional studies of subtle effects were required to fully validate and trust the predictions of the hemisphere mixing model. But all checked out nicely. At the end of the day, the
data in the signal region is used to search for a HH signal, as shown in the graph below.
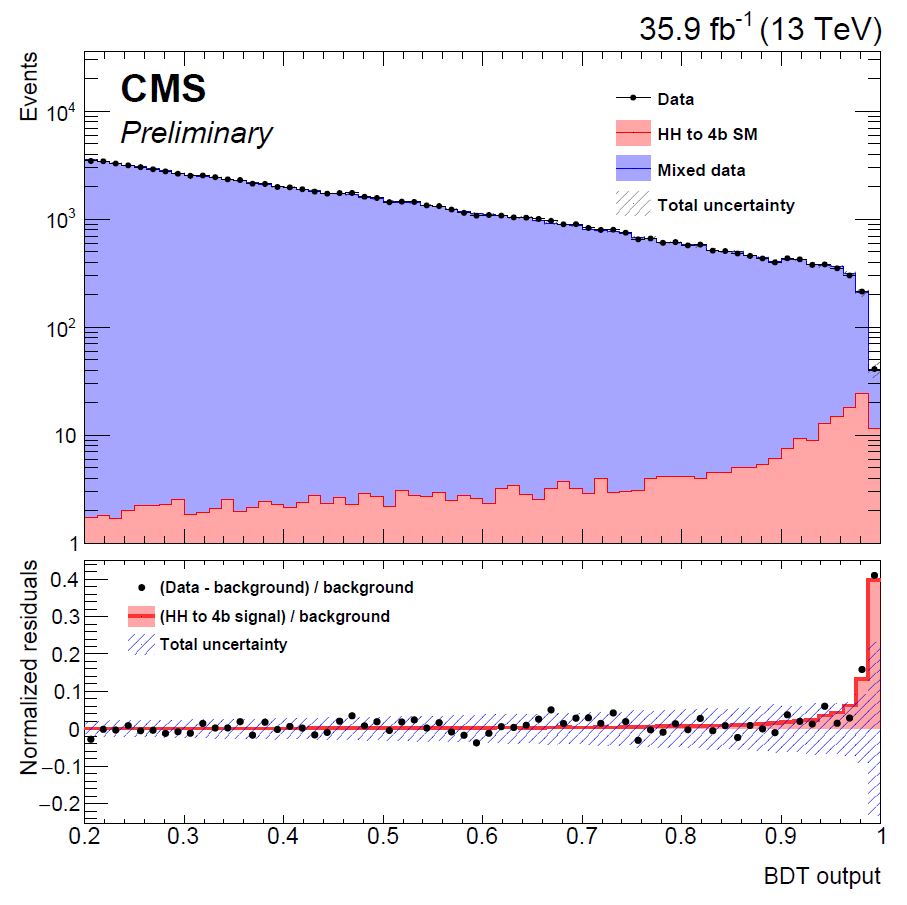
The top panel shows the data with overlaid pre-fit shapes of the background model (in blue) and signal (in red, normalized to the SM predicted rate). The bottom panel shows that after the fit the data, once subtracted of the background component, has a small signal-like excess at high BDT output; the red histogram shows in comparison how the Higgs pair-production signal would look like, normalized to the best-fit result (which corresponds to a rate of about 40 times the SM prediction). The fluctuation is within two standard deviations, considering the total uncertainty from the fit (blue hashed region).
Clearly, at this stage the analysis does not have the sensitivity to evidence the expected presence of a SM Higgs pair signal. For that, it will be necessary to wait for Run 3 of the LHC and to combine all searches for di-higgs production. For now all that can be done is to extract an upper limit on the cross section of the process - if the signal were 100 times larger than the SM predicted one, e.g., we would have detected it, while we did not, so we can exclude that possibility.
In the end, due to the small signal-like fluctuation observed in the high-BDT region, the observed limit set by the analysis (74 times the SM) is less stringent than the one expected (37 times the SM rate). The technique, however, is new, and can still be improved. It will be quite interesting to see how it scores when applied to the larger datasets CMS already has in store.
Meanwhile, CMS has also produced a number of other searches for HH events in different final states than the four-b-quark one. And some of them proved to be more sensitive, as in exchange for a lower branching ratio they are ridden by much more manageable backgrounds. The graph below, also a new result, shows the comparison of observed limits on the Higgs pair production rate obtained by the various searches, and their combination. You can find the details of the combination procedure in this document.
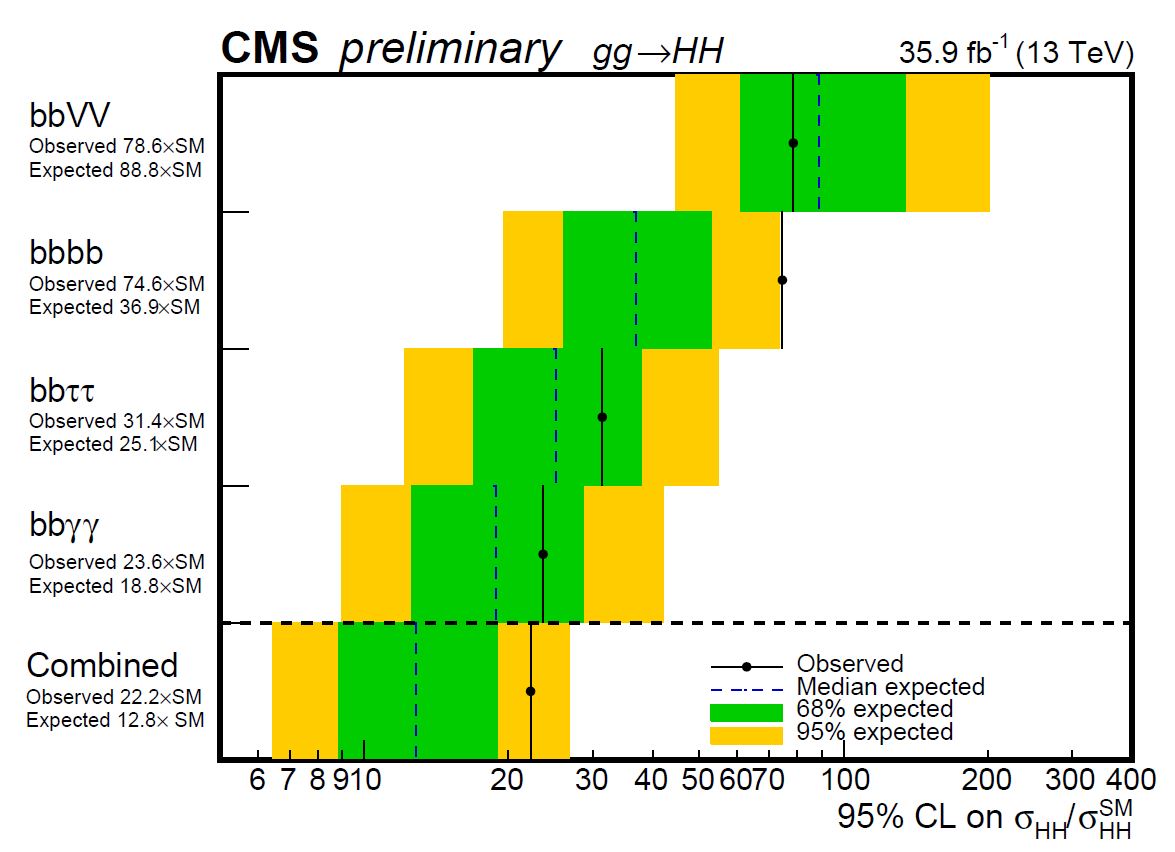
Above, the 95% confidence-level upper limit on the rate of HH production, in units of the SM predicted rate (horizontal axis) obtained by four recent CMS searches, and their combination. All in all, CMS had a sensitivity to exclude rates above 13 times the SM, but only excluded values above 22 times the SM because of observed signal-like fluctuations in some of the analyses.
The graph above, and the mentioned results, may look like a small achievement if you don't appreciate how much work was needed to carry out those analyses with a care of any detail capable of improving the sensitivity, and at the same time checking for all possible sources of systematic uncertainty. I would estimate the total personpower that went into producing the above graph and the included analyses at the level of 40 person-years of work. Yes, particle physics is not a pastime!
---
Tommaso Dorigo is an experimental particle physicist who works for the INFN at the University of Padova, and collaborates with the CMS experiment at the CERN LHC. He coordinates the European network AMVA4NewPhysics as well as research in accelerator-based physics for INFN-Padova, and is an editor of the journal Reviews in Physics. In 2016 Dorigo published the book “Anomaly! Collider physics and the quest for new phenomena at Fermilab”. You can get a copy of the book on Amazon.





Comments