The LHC is...
Let us start with the basics. What is the LHC ? LHC stands for "Large Hadron Collider". Located 100 meters underground at the CERN laboratories near the town of Geneva, at the border between Switzerland and France, the LHC is a 27-km-long synchrotron, a particle collider to be exact. The system of accelerating cavities and superconducting magnets is capable of accelerating trillions of protons at the speed of light in opposite directions inside a vacuum beampipe, bringing them to collide in the core of a few particle physics experiments at a rate of 50 or so collisions every 25 nanoseconds. [Edit: a reader is confused by my statement above that LHC protons travel at the speed of light. Indeed that's inaccurate by 0.0001% or so - that's the speed difference from the speed of light of 7-TeV protons...]
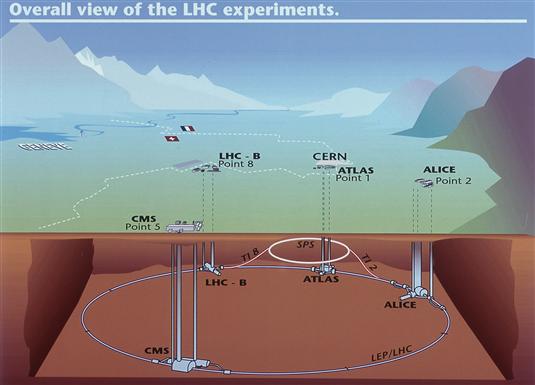
(Above: the LHC collider and its experiments)
As fantastically complex as it is, the LHC is not the only awesome technological marvel sitting underground at CERN. At the four points where the proton beams intersect sit as many giant detectors, ATLAS, CMS, LHCb and ALICE. The first two, in particular, are all-purpose instruments that collect information of the proton-proton collisions in search of hints of new subnuclear phenomena that may manifest themselves in the high-energy proton-proton
collisions.
And IceCube?
Ok, and what is IceCube? IceCube is a detector carved in antarctic ice. Located in the middle of nowhere near the south pole of our planet, IceCube consists of strings of light detectors inserted in holes dug in transparent underground ice. By deploying a large array of such strings, the ice acts as a detector for particles that travel at a speed higher than the speed of light in ice. This happens because light is slowed down when it traverses matter, while energetic particle may not. When a charged particle travels at a speed larger than the speed of light in a medium, it emits a flash of light called "Cerenkov radiation" which is not very different from the sonic boom emitted when a jet plane breaks the sound barrier - the phenomenon is the same from a purely geometrical point of view. The Cerenkov light allows energetic particles impinging in the cubic kilometer of ice watched by the light detectors to be identified, and their energy measured.
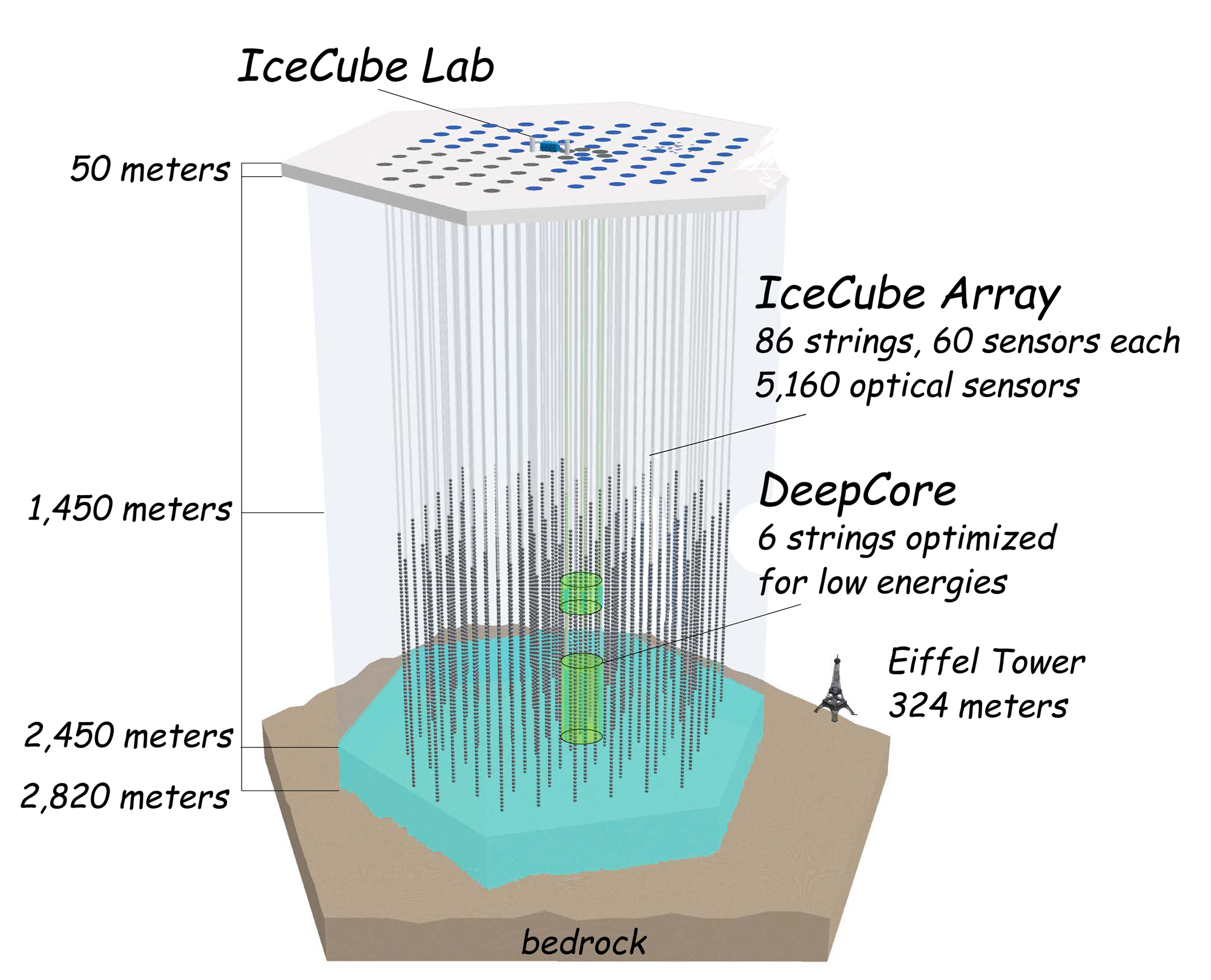
(Above: a sketch of the IceCube detector)
IceCube is meant to study energetic cosmic rays, of which an important component are neutrinos. Neutrinos are neutral, almost massless particles that interact very feebly with anything. Produced in huge numbers by weak interactions in the core of stars, neutrinos can travel for ages through matter without being stopped or slowed down. Because of that property, the neutrinos that are produced by proton-proton collisions in the core of ATLAS and CMS fail to get detected by those apparata, and escape unseen.
Neutrinos
The dominant process that produces high energy neutrinos at the LHC is the creation of a W boson. [Edit: a friend and colleague suggests that I should specify here how neutrinos are also produced, in collectively larger numbers, by weak decays of bottom and charm quarks produced in LHC collisions; however, they have a smaller energy spectrum and are less straightforward to collect. So let's carry on with real W boson decays.]
The W boson is the mediator of weak interactions. It is a massive, unstable particle that decays in a trillionth of a trillionth of a second. When it does it may emit an energetic electron and an electron neutrino (11% of the time), or an energetic muon and a muon neutrino (another 11% of the time). Other decays are less easy to identify in the detectors, but electrons and muons are seen with high effectiveness.
The Question
So, the question one might ask is: okay, those neutrinos escape the CMS detector (say) unseen, and all the physicists may reconstruct when that happens is an energetic electron or muon, isolated from anything else, and recoiling against nothing. This is sufficient information to effectively sort out W boson decay signals from other mimicking processes. But can those neutrinos be seen when they, by chance, end up crossing the cubic kilometer of ice that makes up the IceCube detector?
It is fun to carry out the calculation implied by the above question, but if you have never done something similar you may get lost quite quickly. It is my job today to walk you through the order-of-magnitude estimate of how often does it happen that a neutrino, produced by a decaying W boson created in a proton-proton collision in the core of the CMS detector at CERN, ends up whizzing through the IceCube array and produces a charged-current interaction there, which possibly allows IceCube to record its energy and direction.
[One word of warning: as all the calculations here are done by heart and on the fly, there's a high chance that some order of magnitude has been overlooked in the process. You are welcome to point out mistakes in the comments thread]
First of all, we need to compute how many W bosons are produced at the LHC. We will consider the whole data-taking campaign called "Run 2", which took place in 2016-2018 and allowed CMS and ATLAS to each record an integrated luminosity of 150 inverse femtobarns. Am I running too fast? Integrated luminosity is just a fancy quantity, expressed in even fancier measurement units, the "inverse femtobarns". Luminosity sizes up the number of collisions that have collectively taken place, and actually allows us to get what we want very quickly. Trust me and allow me to explain.
Nanobarns, femtobarns, and similar very small buildings
A positive W boson is produced at the LHC with a cross section of 100 nanobarns. This is effectively an area (a tiny one at that) that sizes up how likely it is that two colliding protons end up producing the W+ boson. If we multiply that number by the integrated luminosity collected by CMS, we get the number of produced W bosons. The calculation goes as follows:
100 nb x 150 fb^-1 = 100 x 150 x (1 nb) * 1000000 nb^-1 = 1.5*10^10
So we get 15 billion positive W bosons. Easy, ain't it? As for negative W bosons, they have a smaller cross section (they are negative, so it's a bit less likely that they get produced when you hit the positively-charged protons agains one another): their cross section is 80 nb, so in total we get 12 billion negative W's.
Now, only two ninths of those bosons can be detected with high efficiency - remember, we want W bosons to decay to electron-neutrino or muon-neutrino pairs. This occurs globally 22% of the time, so in total the useful W+ are 3.3 billion, and the useful W- are 2.6 billion.
I won't lie to you: CMS does not even get close to recording all these events; in fact, on one side they are too frequent -and too little informative- to allow their recording by the data acquisition system (at a total cross section of 100x0.22+80x0.22=40 nb, in high-luminosity running conditions they get produced at a rate of 2000 per second, while CMS can record overall no more than half that rate); on the other, they are not interesting enough to warrant the effort. But for the sake of arguing - and since in principle we could store all the data if we compressed it a bit - we can continue our calculation.
A W+ decay produces a neutrino, while a W- decay produces an antineutrino. It so happens that the former have twice the cross section of the latter when interacting with atomic nuclei. So we keep the number of neutrinos and antineutrinos (3.3 and 2.6 billions) separated.
A bulky, but very distant target
How many of those neutrinos ended up crossing the IceCube detector between 2016 and 2018? We need to consider that the decay of the W bosons is roughly isotropic - or in any case, we will not bother discussing the relative orientation of the LHC beams with respect to the ideal line going from CERN to IceCube. But the distance matters: it is about 10000 km. At such a distance, IceCube intersects a tiny fraction of the solid angle. In fact, out of the 4*pi*R^2 = 12.6*10^8 km^2 surface of a sphere of 10000 km radius centered at CERN, only one square kilometer is instrumented with IceCube light detectors. This makes the "acceptance" of IceCube for CERN neutrinos equal to a meager 0.8 billionths.
We end up with the rough estimate that overall, only 0.8*10^-9 x 3.3*10^9 = 2.7 neutrinos and 0.8*10^-9 x 2.6*10^9 = 2 antineutrinos made it through IceCube after being produced in the core of CMS together with an electron or a muon! Beware, here I do not even bother considering that a fraction of those neutrinos will have a chance of being stopped by the intervening matter they traverse on their way to Anctartica: that is a very small fraction anyway.
4.7 of them made it!
At this point you might already have lost interest - even if IceCube were a perfectly performant detector and it had been taking data uninterrupted during the data taking periods of CMS, a signal of 4.7 neutrinos would never be discerned from backgrounds looking like neutrinos coming from the CERN whereabouts acquired during three years! But let's get to the bottom of it.
Neutrinos have a very, very small cross section for interactions with nucleons: these equal, for a E=100 GeV neutrino or antineutrino (E is the order of magnitude of the energy the neutrinos emitted in W decay possess), about 680 femtobarns and 340 femtobarns, respectively. But one kilometer of ice is a lot of nuclei: let us calculate what it collectively amounts to.
The number of nucleons in a cubic centimeter is roughly twice the Avogadro number, 6*10^23. So in crossing 10^5 cm of ice, we can express the number of nucleons per square centimeter as 1.2*10^29. Since a square centimeter is 10^39 femtobarns (look it up if you don't trust me), the number of nucleons is 1.2*10^-10 per femtobarn. By multiplying this number by the above cross sections we get:
N(neutrino interactions in IceCube per 100 GeV neutrino) = 680 fb * 1.2*10^-10 fb^-1 = 8*10^-8,
N(antineutrino interactions in IceCube per 100 GeV antineutrino) = 4*10^-8
Voila. Now, we take the 2.7 neutrinos and multiply by 8*10^-8 to get 2*10^-7, we sum 2 antineutrino multiplied by 4*10^-8 to get 8*10^-8, and the total is less than 3*10^-7. The expected number of electron and muon neutrinos originated at CMS during Run2 which crossed the IceCube detector and produced a charged-current interaction there, making themselves visible (through the Cerenkov light that the produced electrons or muons yielded) is 0.0000003. A five-sigma effect!
No, I did not make it up, nor did I adjust the many numbers of this article which you no doubt won't go out checking. The result is surprising: the chance that we could, at least in principle, combine (through precise timing information between the CMS detector and IceCube, and careful directional information extracted from the recoiling electrons and muons) the signal of a high-energy electron or muon in CMS with the signal of a 100-GeV or so neutrino charged current interaction seen by IceCube, even admitting that the detector kept watching its ice for the whole duration of the LHC run 2, is of the same order of magnitude as the chance to obtain by a random fluctuation a signal of the strength of the original Higgs boson signal found by CMS in 2012. Food for thought, no doubt!



Comments