More than specific good leads for new research, the thoughts I share below indicate a diagonal way of thinking at our design problems, so I do not fear of getting scooped if I share them here. Besides, any one of the topics below requires significant investment of person-power and resources, and none of them is guaranteed to produce a groundbreaking result at the end, so spilling the guts here is quite safe! In fact, I am reminded of a very nice advice from Howard Aiken: "Don't worry about people stealing your ideas. If your ideas are any good, you'll have to ram them down people's throats!"
The general context is the one of thinking hard about ways to improve our particle detectors for the future tasks that we want to tackle (fundamental questions in particle, astroparticle, neutrino and nuclear physics, to be specific, but also derived spinoffs in industry), by exploiting whenever possible the new software technology available today - and tomorrow!
[The last specification is very important, although I cannot focus on it here: our detectors take long time to be commissioned, so it is crucial to align their design choices to the capabilities of future AI reconstruction and information extraction procedures.]
What can you get?
In proposing a continuous scan of the parameter choices in detector design (a huge space of possible choices and configurations, given an envelope of budget, commissioning time, and other external constraints), I am often led to discuss what kind of gains we may expect to reach over paradigm-driven, experience-driven experiment design, i.e. the way we have been doing this business until now, with very few exceptions. The question might be, "Even assuming you can simultaneously optimize hundreds of parameters and choices, is there really something to gain?"
One way to answer this question is evidence-driven. E.g., by working full time for eight months on a simulation/reconstruction/optimization, and writing 8000 lines of code in the process, then publishing a 60-page article, I have recently proven how an improvement by a factor of two in the relevant metric (the optimization target of the experiment in question, MUonE) could be obtained over the design originally proposed by the MUonE collaboration.
A factor of two in relative resolution is gigantic - it basically corresponds to saving 75% of the original cost, or having to run for a fourth of the time (say, one year versus four years), as data precision for Poisson processes scales with sqrt(N). The graph below is the summary of my results, where the relevant metric (the relative uncertainty in the squared momentum transfer q^2 of muon-electron collisions, as a function of q^2) is shown to decrease twofold after the optimization, especially where it is most important (high energy, i.e. the right part of the graph).
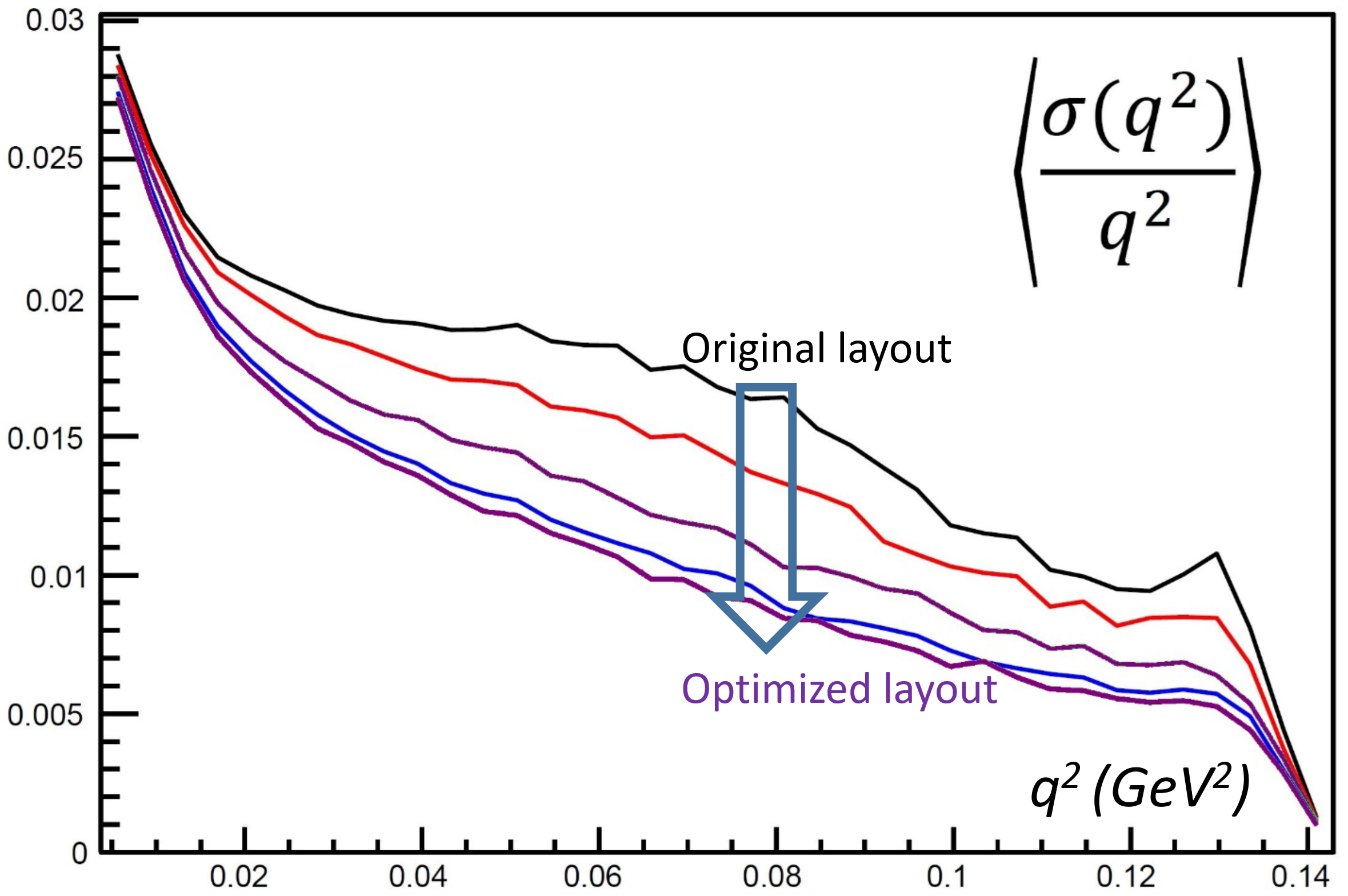
I have discussed this work elsewhere and I will not comment further, but it is obvious that if for a simple experiment (MUonE is studying a very straightforward process, only trying to do so with very high precision) we can double the precision with a relatively simple optimization study, it is very safe to assume that at least as big gains await us if we consider much more complex setups. I could also cite another couple of similar studies that reach very similar gains, but let's stop this here.
The other way to answer the question is a bit longer to explain, but let me try. We need to first of all consider how today the advanced deep-learning algorithms we have so far used for "simple" and well-defined tasks, such as classification to distinguish small signals from large backgrounds in LHC analyses, or anomaly detection, or pattern recognition in dense environments, can be applied with great prospects to the problem of end-to-end detector optimization. How can that be done?
We need to couple this question with another bit.
The second answer
There is a more specific way, albeit a diagonal one as I was mentioning, to think at how we could improve our instruments. We have learnt to exploit the curvature of charged particles in magnetic fields to measure their momentum, and built performant tracking devices that do precisely that. We have perfected dense detectors where charged and neutral particles alike can release all their kinetic energy and yield a measurable signal proportional to their energy. We have exploited even subtler phenomena such as Cherenkov radiation, ionization energy loss, etcetera, and whenever we did we gained some precision with our apparatus. But we are not done.
What I am thinking at is that there are some nuisance parameters that systematically affect our measurement of particle reactions, and that worsen our capabilities of attacking the "inverse problem" of inferring the underlying physics of the particle collisions from the observed electronic signals in our detectors. Every one of these nuisance parameters has a connection to something we do not know, or to some unmeasurable or unmeasured phenomenon that bears relevance to those we want to study.
Also, we have learnt that if we manage to constrain those nuisance parameters - either internally, by targeting their measurement in parallel to the measurement of the parameters of interest, or externally, by performing calibrations or independent measurements to constrain them - we win precision on the parameters we want to learn about. This is very well understood now, and the analysis tools that were deployed for the Higgs search by ATLAS and CMS in 2011 are capable to trace very clearly the interrelation of these nuisances with the physics we care about.
So the way to think about improving our detectors that is the topic of this post is: if there is a nuisance parameter, there is something to gain if we either build in our detectors the capability to handle and estimate it, or if we find ways to measure our physics phenomena by constructing observable quantities that "rotate away" the effect of the nuisances, i.e. that become robust to the imprecise value of those nuisance parameters.
An example of the second approach is the INFERNO algorithm which Pablo de Castro and I have developed a couple of years ago. Not surprisingly, INFERNO exploits differentiable programming tools to inject in a classification problem, handled by a neural network, the knowledge of the true optimization target of our measurement, as well as the existence and effect of nuisance parameters on that target. The network is thus enabled to learn a data representation, and a dimensionality reduction, which maximally decouples the results from the unwanted nuisance parameter uncertainty.
Nuisances to exploit
Below I offer a few ideas I came about with when thinking diagonally at our detector optimization tasks. The examples below are not thought at very deeply, but they should give an idea of a fruitful (I think) way of interpreting the problems.
1 - One example that has been duly exploited since ages, but which is an easy way to understand the diagonal thinking, is the one of nuclear de-excitations in calorimeters.
In a calorimeter the energy of incident particles is converted into electronic signals that are proportional to it, by exploiting the multiplication process taking place as the incident particle creates others, gradually losing its original energy. Although below I speak about hadrons, let us consider electromagnetic showers first, to explain how these instruments work.
Electrons and photons can be measured precisely by exploiting the electromagnetic shower that takes place when these particles interact with strong electromagnetic field of heavy atoms inside dense materials. An electron, e.g., will emit an energetic photon, and the photon will later materialize into an electron-positron pair, and so on - at the end of the shower, the number of particles produced is proportional to the incident electron energy.
For hadrons life is not so easy. Protons, pions, kaons, neutrons that impinge on a hadron calorimeter suffer from the existence of processes that do not yield a proportionality between incident energy and number of released secondaries. These processes are typically "nuclear de-excitations" and recombinations that fail to generate readable electronic signals in the active material.
So the idea exploited already at the end of the last century was to build hadron calorimeters with Uranium. Uranium nuclei, when broken by a hard interaction, will release some extra energy from their fission. By calibrating the response, one may get back the energy lost in the processes that do not produce a proportionality of secondary particles in the shower. This "calorimeter compensation" has been exploited in a number of modern detectors.
So the above is an example of how a nuisance can be turned to our advantage, improving the performance of our instrument. But let us talk about bringing this idea further.
2 - At high energy, particles radiate some of their energy away in the form of soft photons. In a calorimeter this energy can be measured and is not a problem, but for a muon, e.g., things are different - the standard way of measuring a muon's energy is by its bending in a magnetic field. This cannot be done when the muon is too energetic (say above a few TeV), because at that energy the muon does not bend any longer in even the strongest magnetic fields.
However, something else happens in that regime: the soft photons radiated by the muon can be used to measure its energy with higher precision that what the curvature can provide. This has been demonstrated in a paper (actually, two papers - one using CNNs and another using the k-NN algorithm for the regression of muon energy from the pattern of soft photon radiation in a granular calorimeter) we published recently. So here is another example of how exploiting subtle physical phenomena that may be a nuisance to our main measurement task can be turned to our advantage.
3 - Trackers of charged particles have traditionally been built by using very light material - gas mixtures or very thin layers of sensitive detectors (silicon). The reason is that when a charged particle hits a nucleus, it can produce a reaction that creates multiple secondaries. These become hard to reconstruct and the energy lost by the incident hadron reduces our capability to measure its energy by the curvature of its track. However, with deep learning coupled with precise sensors we may be able to reconstruct nuclear interactions. What do we gain? We potentially gain information about the originating particle species, as different hadrons (protons, pions, kaons, neutrons) have different probabilities to originate a nuclear interaction.
The above idea can only be exploited if we build in our reconstruction software two things: one, the capability to effectively reconstruct these nuclear interactions; and two, the flexibility to exploit probabilistic information on the particle identity in the estimation of the total energy flow in the event. So this is also an example of how new software ideas and hardware ideas must play in together: to exploit the phenomenon one needs both to perfect the event reconstruction (by injecting probabilistic information at all levels) and to optimize the layout of the tracker by inserting, in suitable spots (e.g., at large radius, when most particles have already been tracked reasonably well) a dense layer followed by a precise tracking layer.
4 - A similar idea is to exploit our knowledge (and insufficiently precise knowledge, a.k.a. modeling systematics, a.k.a. nuisance parameters) on the fragmentation function that describes how quarks and gluons end up producing streams of hadrons of different energy and type. When we reconstruct jets with the so-called "particle flow algorithm", which is state-of-the-art at the LHC, we would benefit greatly from knowing that an incoming track is, with 70% probability, a proton, or that another one is more likely a pion. As mentioned above, by rewriting particle flow reconstruction as a probabilistic program we can use this information. By coupling the a-priori knowledge of what is the chance that different hadrons with different momenta hit the calorimeter (extracted from our fragmentation function models) we can certainly improve the reconstruction task.
5 - Parton distribution functions (PDF), the mathematical functions that model the probability that inside a proton you find a quark or a gluon with a given fraction of the proton's energy, today come endowed with a recipe to estimate the impact of their uncertainties (40 or so eigenvectors, the last time I looked). As PDF uncertainties play heavily in the precision of our measurements, it seems very intriguing to consider, given a parameter of interest, what particular combination of observable quantities is the most robust to their effect, by training a ML algorithm to find the subspace where the answer we search is the least affected by the variations of the PDF. By doing this study in a systematic way we could learn that there are specific observables extractable from our event reconstruction procedures which are more robust than others. We sort of know some of this already, but the next step is to consider if this may have an impact in the way we construct our instruments, as we certainly want to measure things that are more robust to this particular uncertainty.
I stop here, but I guess I have clarified how by thinking at our systematic uncertainties (nuisance parameters, in statistics terminology) not as enemies but as friends, we may have a way to inject in our detector design the flexibility to exploit the subtle physics processes that govern them, to our advantage. Again, it seems crucial to think at this before the design of our instruments is frozen, because even if we presently have no capabilities to perform the precise reconstruction required for some of the above ideas to work, we may well have it by the time the experiment goes in commissioning - 10 or 20 years down the line!
---
Tommaso Dorigo (see his personal web page here) is an experimental particle physicist who works for the INFN and the University of Padova, and collaborates with the CMS experiment at the CERN LHC. He coordinates the MODE Collaboration, a group of physicists and computer scientists from eight institutions in Europe and the US who aim to enable end-to-end optimization of detector design with differentiable programming. Dorigo is an editor of the journals Reviews in Physics and Physics Open. In 2016 Dorigo published the book "Anomaly! Collider Physics and the Quest for New Phenomena at Fermilab", an insider view of the sociology of big particle physics experiments. You can get a copy of the book on Amazon, or contact him to get a free pdf copy if you have limited financial means.






Comments