However, in this post I will give an example of something qualitatively different to providing an improvement of a measurement: one where a deep convolutional network model may extract information that we were simply incapable of making sense of. This means that the algorithm allows us to employ our detector in a new way.
The case I am discussing is one which I have studied in some detail in the past 18 months, together with a few colleagues who are expert in machine learning and detector signals reconstruction. It involves the question of whether we may rely on electromagnetic radiation emitted by energetic muons to estimate the muon energy.
Muons are heavier replicas of electrons. If they are endowed with significant momentum, they can penetrate large amounts of material leaving only little energy behind, and getting scattered only a little bit off their original path. Because of this penetrating power, muons are detected by the outermost detection systems in particle collider experiments, in a region where all other particles have hit nuclear matter of the calorimeters and have thus been stopped. E.g., look at the cutaway view of the CMS detector below: the muon system is the one on the far right, and is usually reached only by muons.
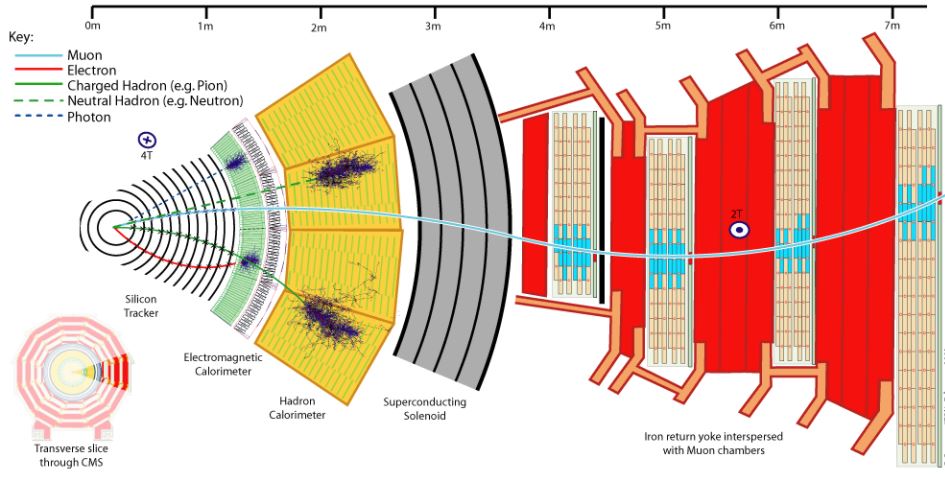
Because of their peculiar properties, and because of the rarity of their production in proton collisions at the Large Hadron Collider (LHC), muons are precious signals of rare, interesting phenomena. We detect them with muon chambers, but in truth we rather rely on the inner tracking system to determine their energy. This is because their energy can be assessed by measuring the amount of curvature their trajectories withstand in a strong magnetic field, which is produced by the solenoid (the grey barrel in the picture above).
When muons are very energetic, they curve less. In fact, there is a linear relationship between the energy of the muon and the radius of curvature, given a fixed magnetic field. When a muon reaches an energy of 1 TeV (one teraelectronvolt, or about 7% of the total collision energy of the LHC) its radius of curvature in the ATLAS detector (which has a 2 Tesla magnetic field in its core) becomes of 1660 meters. That's a big circle, and in fact the muon trajectory at that energy ceases to be distinguishable from a straight line - we therefore lose our capability to measure the energy of highly energetic muons, which by the way are the rarest and most precious potential probes of new physics processes we have in LHC collisions!
In reality things are not so dramatic - the energy of a 1-TeV muon can still be measured with some 10-20% resolution, so we can still do business. But the linear relationship also means that the resolution scales linearly with momentum. For a 2 TeV muon the resolution doubles, and for a 4 TeV muon it reaches 80% in the worst case - which means that you can't really tell a 4-TeV muon from a 2-TeV one very effectively. While at the LHC this problem is not keeping us awake, what will happen in a future, more energetic collider?
If the LHC, with its 14-TeV collisions, produces muons that exceedingly rarely surpass 3 or 4 TeV, a future circular collider might produce collisions of 50, 80 TeV, and muons could appear with momenta of 10 TeV and above. At that energy, the magnetic bending is really ineffective as an energy measurement. But on the other hand, very energetic muons start to behave like their lighter cousins, electrons: they radiate more electromagnetic energy when they traverse dense media.
We exploited this "relativistic rise" in the electromagnetic radiation off energetic muons to verify whether it is possible to measure muon energies in a granular calorimeter. A granular calorimeter records the energy left by the particles in small cells, so that for a very energetic muon you may get to read out a few hundred independent energy depositions along the track and a little off it. What you can do is to add up all the energy depositions, coming up with an estimate of the total energy release, and use the latter to infer the muon energy. But this is highly ineffective, as even a multi-TeV muon often leaves only 1 or 2 percent of its energy in a thick calorimeter, and the result is subjected to enormous fluctuations.
Deep learning methods can treat the problem of inferring the muon energy as one of regression in a multidimensional space - the space is spanned by all the coordinates and energy depositions that the muon gave rise to. The question then is: can we exploit the _pattern_ of the energy deposition of muons to add information to the sheer total energy release, and improve our energy estimates?
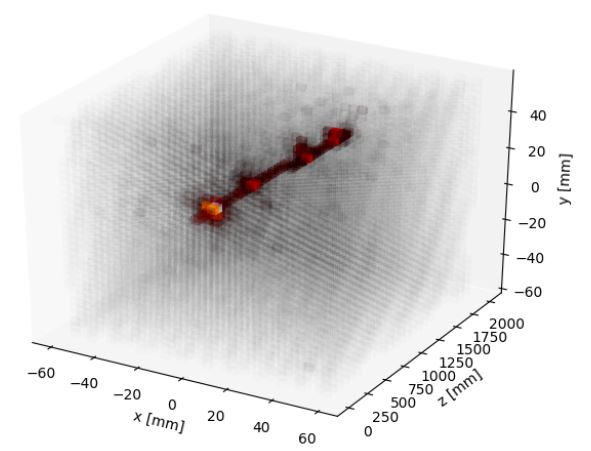
The answer is, surprisingly, yes. We demonstrated it and documented our results in an article that has just been accepted for publication in the journal JHEP (the article is however still presently only available as an arxiv posting). Our study makes use of simulated muons impinging in a very high-granularity, homogeneous calorimeter made of lead tungstate crystals (the same material of the CMS detector's electromagnetic calorimeter). A muon impinging in such a device looks like the image below:
We employed a very complex convolutional neural network architecture for the regression task. Our study is indeed rather difficult to describe in detail here, but I want to show a "money plot" which summarizes the results of our efforts. Before we get there, let me explain that the quantity of interest in a measurement of muon energy is the total resolution, which can be contributed by variance and bias.
Indeed, let's examine the resolution (on the vertical axis) on true muon energy (on the horizontal axis, in GeV) produced by the deep learning model, which is shown for different input data: 1) if we only use the total energy read out in the calorimeter (blue), 2) if we also use high-level variables that a human (me) could cook up, and which somehow trace the peculiarity of the shape of the energy deposition pattern (orange), 3) if we use the full spatial information provided by the granular calorimeter (green), and 4) if we use that along with the high-level variables (red).
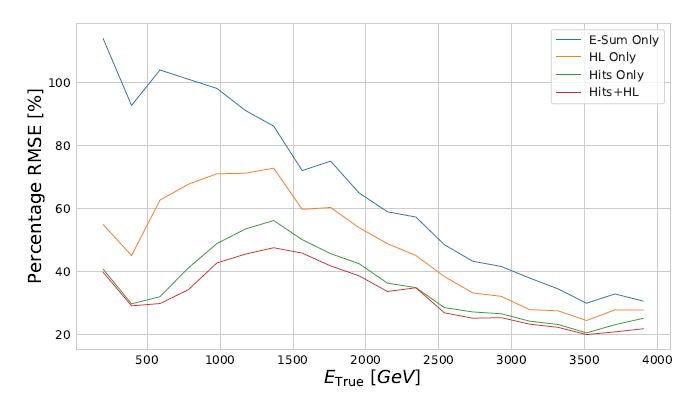
As you can see, the resolution offered by a calorimeter that disregarded the spatial pattern of energy deposit (blue) is good but not great: for a 3-TeV muon, e.g., it is of the order of 40% (at 3 TeV, by comparison, a 2-Tesla magnetic measurement would typically produce a 60% resolution, so a worse result already). But if you add spatial information as a human can do, you get to some 30%. And if you unleash the full power of a neural network, you get closer to 20-25%. All of this means that in the future, we will still be able to measure muons of extremely high energy in a collider, even if our magnets cannot be built with arbitrarily large fields (in fact, the 4-Tesla of CMS are about as much as we can reasonably get, since the technological hurdles of produce larger fields in very large spaces are enormous).
Also interesting is to ask ourselves what would happen if we combined the calorimetric measurement we obtain through our deep learning model to the measurement that a magnetic bending may provide. The latter "breaks down" at high energy, while the former should actually improve at high energy (due to the "relativistic rise" I mentioned earlier). In the end, the combination of a tracker and a finely segmented calorimeter produces a good measurement (better than 30%) across the board, from 0.1 to 4 TeV of energy (and above):
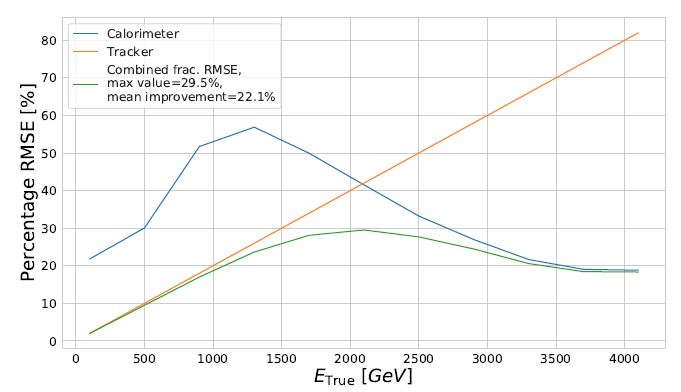
In summary, deep learning can significantly boost our measurement potential, if coupled with instruments that provide highly granular information which we would otherwise be unable to fully exploit. Even better, they sometimes provide new solutions to problems that would otherwise seem untreatable.
I of course offer congratulations to the co-authors of this study: Jan Kieseler (CERN), Giles Strong (INFN-Padova), Lukas Layer (INFN and University of Naples), and Filippo Chiandotto (University of Padova). Well done folks, we pulled it off!
---
Tommaso Dorigo (see his personal web page here) is an experimental particle physicist who works for the INFN and the University of Padova, and collaborates with the CMS experiment at the CERN LHC. He also coordinates the MODE Collaboration, a group of physicists and computer scientists from fifteen institutions in Europe and the US who aim to enable end-to-end optimization of detector design with differentiable programming. Dorigo is an editor of the journals Reviews in Physics and Physics Open. In 2016 Dorigo published the book "Anomaly! Collider Physics and the Quest for New Phenomena at Fermilab", an insider view of the sociology of big particle physics experiments. You can get a copy of the book on Amazon, or contact him to get a free pdf copy if you have limited financial means.





Comments