True, I am older and have seen and done much more in outreach than I had until 2012. For one thing, I have 12 more years of blogging experience (but I already had 8 back then); also, in these past 12 years I have given something like 30 public lectures to students or general public, on topics ranging from the Higgs boson discovery to artificial intelligence. But the added experience has probably only refined my skills, not necessarily deepened my understanding of the matter.
In the end, I decided that the old article, which had been rather unfortunate -probably in the proceedings book where it landed it has never been read a single time- deserved to be revamped, and I invested some time in reviewing critically what I had written, then improved it. The result is going to appear next month in the next issue of the magazine, but I will share below a quick and dirty translation (sorry for the rather unrefined translation, courtesy google - with minimal interventions).
-------------------------
The Analogy: a Powerful Instrument for Physics Outreach
The analogy is a widely used rhetorical figure in written and spoken language. It is sewn in the very fabric of our language (sometimes mixed to hyperbole, or other mechanisms). Often we do not even realize we are thinking by analogy: phrases like “He loves his cat like a daughter”, or “I feel as if the world had collapsed over me” come spontaneously and allow us to communicate effectively in a figurative manner of the characteristics of the source (the cat in the first example,
or myself in the second) through the evocative power of the target of the analogy (the daughter, or
respectively me under the rubble).
If you look closely, we all make on a daily basis use of analogies, small or large, stated or imperceptible, in composing reasoning in oral or written form. Although we might not be conscious about it, we also use them constantly in actions that do not pass through a verbal phase (for example, when we use for a contingent purpose a tool designed for a different function). The analogy is indeed one of the most powerful cognitive processes, and is considered one of the fundamental tools of learning. Through analogy we are able to extrapolate our knowledge and skills to more complex systems, reducing their difficulty.
In the exact sciences, however, we have the problem of not being able to deform at will some parts of the system: if we ignore the quantitative aspect of physical laws or mathematical equations around which we would like to adapt our or others' intuition, to make them more accessible, we usually miss an important part of the explanatory power of the analogy that we construct. Or if in the absence of anything better we settle of imperfect analogies, which describe only part of the functionality or characteristics of the concepts for which we seek a simplification,
we risk confusing instead of clarifying. It therefore becomes useful to ask whether there exists a
recipe, or if there are at least some guidelines, to decide whether an analogy is useful or not.
I will try to answer the question here within the scope of the popularization of particle physics, a field in which I have accumulated some experience, or at least a habit. The place where I collected most of the information on power and on the limits of analogies created to explain concepts of particle physics, over the past 20 years (twenty years!), is my blog, “A Quantum Diaries Survivor”. The blog receives over one million visits per year. Even if over the years I have slowly decreased my
dissemination commitment with that medium, due of understandable shifts in my work priorities, I still publish there several articles per month.
One of the recurring themes in these articles is to comment and explain to a mixed audience (partly made up of students and researchers, but predominantly made up of simple readers interested in science but not provided with a specific background in fundamental physics) recent physics results coming from experiments to colliders, and other topics related to those. Recently, in correspondence to a greater research commitment towards computer science topics, I shifted the focus to articles discussing new techniques in machine learning and artificial intelligence, nevertheless maintaining fundamental physics as the goal of developments and techniques discussed.
During the years of my greatest dissemination commitment, which coincided with the years when blogs were still very fashionable, my blog articles used to receive an average of a dozen comments in the first days after online publication; the comments usually sparked interesting and sometimes controversial discussions , which enriched the value of the published pieces. The comments were and they are the main tool for understanding how suitable the texts are for readers and their background, and whether the concepts covered and the expository language are within their reach and respond to their interest.
In fact, commentators often offer, directly or indirectly, useful information on the effectiveness of an explanation. Reasoning on the most effective methods for explaining difficult physics concepts, in a continuous attempt to bring taking non-experts by the hand towards understanding the importance and meaning of the measures in particle physics, I thus found myself thinking about the construction of the analogy.
To start a discussion on the analogy as a communication tool, it is appropriate to consider a well-known phrase by Albert Einstein:
“In the explanation of physical phenomena, everything should be made as simple as possible, but not simpler than that”.
A danger is therefore excessive simplification: in an attempt to make familiar what is foreign to us, we include too little detail in the analogy, deteriorating the correspondence between target and source and preventing understanding of the latter; or worse, we distort physical reality to make the rhetorical figure work, thus adapting our goal to the tool instead of the other way round. We can put Einstein to the test of his standards of him citing an analogy of his invention:
“You see, wire telegraph is a kind of a very, very long cat. You pull his tail in New York and his head is meowing in Los Angeles. Do do you understand this? And radio operates exactly the same way: you send signals here, they receive them there. The only difference is that there is no cat.”
This analogy is undoubtedly simple. But is it as simple as it needs to be, or too simple? This depends on the listeners you are addressing: for a child the explanation is perfect, while if offered to students of a course in communications technology it would be embarrassing. Hence the degree of complexity
of an analogy, just like the level in general of an explanation, must be calibrated appropriately.
It therefore looks reasonable to ensure that we have two things very clear in our mind when constructing an analogy to explain a concept in physics: first of all, what the skills of our listeners are; and secondly, what do we want the listeners to hear really internalize when exposed to the analogy that we build. It is therefore useful to try to recognize some factors that allow us to judge
if an analogy is appropriate for ours listeners, if it allows the goal to be achieved, or if it is too complicated, and potentially distracts from the goal. We may focus on these factors through the analysis of a example: a well-constructed analogy but which in reality has no real explanatory power.
Let us take the explanation of the breaking of the electroweak symmetry through the behavior of diners ad a circular table, an analogy due to Abdus Salam, one of the theoretical physicists who originally formulated the standard model of electroweak interactions. So let us imagine to try to explain how the choice of one of the possible vacuum states of a constituted physical system from a doublet of complex scalar fields ϕ = [ϕ1 + iϕ2, ϕ3 + iϕ4] breaks the symmetry of the system. We could try with the following text:
“You are at dinner and, together with the others diners, sit around a table round. Notice the vegetable dish it is located to the right of your plate, but also to the left of the plate
diner seated to your right. You don't know which dish to take, until until someone takes that to the own right. Now that the choice was Once done, the system is no longer degenerate, and there is only one logical answer to what that is your vegetable dish! Similarly, in the Lagrangian of the Higgs field there is a degeneration, a multitude of equivalent possible states, and the choice of a particular value of ϕ determines what the physical realization is of the system."
Personally I have always found this analogy not very effective, despite its elegance. If we carefully examine the way we use it, in fact, it becomes apparent that we are spending maybe twenty seconds to create in the listeners the image of the laid table and to place them vis-a-vis with the dilemma of which vegetable dish to choose, implicitly identifying them with the unstable quantum vacua. But what do we obtain with this operation? Have we in any way explained how this choice occurs, or what happens to the degrees of freedom that are transferred from the Higgs field to the mass of vector bosons? These questions remain in the air and cannot find response, as there is no correspondence in the construction between the physical concepts they evoke and the elements of the laid table. That which we have explained is actually uniquely in what consists the removal of a degeneration. But there was certainly no need to set a table to achieve this modest result!
It is therefore appropriate to always ask ourselves what is the actual value of an analogy. In the specific literature the value of an analogy is usually identified with its predictive power of the unknown characteristics of the source. This can be evaluated using properties of the similarity between source and target that they are linked to the strength of the analogy that can be drawn among them: the relevance of the similarities to the characteristic or function object of logical inference, their number, and their variety. However, in case of educational applications, there are additional units of measurement that provide an important evaluative meter. For example, critical issues are the listeners' familiarity with the target, how brief the necessary description is, and how well known is the part of the target that is the object of the inference. Those mentioned are elements that depend on the listeners we are addressing to; a more general element is instead how much actually coincides, in target and source, the phenomenology of the part object of the inference. The similarity might in fact be only accidental, or lexical, and render the analogy ineffective or sterile.
In the example of symmetry breaking, the degeneracy removed from the choice of the dish or from the state of the vacuum does not possess characteristics able to extend the deduction. Where are the analogue of the Goldstone bosons removed by the choice? It would be nice to be able to say that the first diner ate them, but it doesn't work. By contrast, in Einstein's analogy seen above, in addition to the predictive power (signals can propagate both through a wire and along the nervous system of a cat) the explanatory power lies both in the familiarity of the target as much as in the predictability of the cat's response (meowing) to solicitation (pulling its tail). Furthermore the phenomenology is coincident, a quite surprising fact that embellishes the construction: in fact in both cases, cat and telegraph, it is an electrical signal what propagates!
It is also useful to identify some typical problems that poorly constructed analogies can present, and which make them ineffective or unsuitable for the intended purpose. First, it should be noted that the analogy must have as its objective the one of extending our understanding of the source through the study of a familiar target. Sometimes however the already known characteristics of source and target are very similar, while the ones we want to explain they are not at all similar or poorly lend themselves to a deduction. In other words, the analogy is missing any real deductive power.
Secondly, we need to ask ourselves if it is easy to concentrate on the characteristics object of the inference, or whether rather the chosen target is complicated or present features that risk distracting the listener: in other words, the analogy may not be economical, and can in this case make it difficult
focus on the characteristics that interest us of the chosen target. There is also the danger of looking for too many similar characteristics in source and target, taking too far a good analogy and thus distracting us from the original purpose, missing the objective that we had placed to ourselves.
There may also be contraindications external nature to an otherwise valid analogy. R. Dawkins in his book “The God Delusion” talks about an “ultimate burqa” that allowed us for centuries to see only a small part of the world through a crack; science gradually opened this crack, bringing the hope of one day being able to free ourselves completely from that burqa. This analogy has some merit,
but it can be offensive to a Muslim: caveat emptor.
Another example comes from the office of a gynecologist, who in the definitely noble effort to explain the situation to a patient, launches into the contruction of the following hypothesis: “Imagine that this room is your vagina”. The person who reports this sentence explains: “He should have invented an analogy that did not involve imagining him standing inside my vagina. He caught me so off guard that I couldn't remember which wall was my cervix".
An otherwise good analogy may turn out to be imperfect: an important difference between source
and target can then make fallacious the conclusions that arise from it, if its domain of applicability is not limited. Take for example the famous, and otherwise fruitful, analogy that may be used to explain weak charged current interactions with the help of the knowledge of electromagnetic ones: both interactions act by means of the exchange of a bosonic carrier (a photon in electromagnetism, or a boson W in the weak interaction); this allows us to understand some properties of the source, and also to build quantitative calculation methods in almost perfect correspondence. However the weak hypercharge does not propagate along the fermion lines connected to the emitted or absorbed W boson, as electric charge does. This fact could be erroneously transmitted to those who listen to us if we do not pay attention to limit the application context of the analogy we used.
To conclude, it is useful to note how they exist comparisons between systems that are not related at all of correspondence between them in the above part which the emphasis is placed: these are false analogies. The most common case is when the object property of inference or deduction is the essence of what distinguishes source and target. Taking on mistakenly that it exists in a stage by definition grass to run on, a player could show up at the ice stadium with shoes soccer.
∗ ∗ ∗
I would now like to briefly discuss some examples of analogies, both original and otherwise, used in my blog to explain basic concepts in particle physics, identifying, when possible, their strengths and weaknesses according to the approximate categorization outlined above. Let's start with a rather complicated concept: the intrinsic weakness of weak interactions.
We know that the large mass of W and Z bosons, which mediate such interactions, is the reason for their weak intensity: their mass prevents bosons from mediating long-range interactions, and it is a parameter that determines the intensity of the interaction. We can propose the following text:
"To understand how a massive mediator can be less effective and act more weakly than one without mass, consider a cup of hot chocolate and a chocolate bar: the hot steam disperses around the cup many very small, light particles, which can be easily smelled from a distance. In contrast, the chocolate bar can only release a few small solid flakes of chocolate if you get very close and inhale forcefully. The flakes are more massive and less abundant than the particles that evaporate from the cup, and are therefore incapable of transporting the scent of chocolate far; furthermore, even at a short distance, the smell from the chocolate bar is less intense due to the smaller amount of flakes released when you smell it."
Before discussing the advantages and disadvantages of this analogy, let's see how I used it in the blog, trying to extract the maximum meaning possible from it.
"The behavior of the chocolate odor from the cup and from the chocolate bar can be compared to the behavior of electromagnetic and weak interactions at low energy: the former appear much more intense. But now imagine building a device, a sniffer, that analyzes the odor of solid bodies and liquids in the same way: the test object is vaporized and the spectrum of vapor absorption is analyzed. The sniffer will find that hot chocolate and the chocolate bar have the same intensity of perfume. Similarly, electromagnetic and weak interactions become equally strong at high energy, once the mass of particles of chocolate or flakes, or photons and Z bosons, becomes irrelevant."
It should be noted that despite the explanatory bonus of the second part of this analogy, which introduces a new element (the sniffer) to explain electroweak unification, it would probably have been better to stop at part one: we fell too in love with the analogy and used it to explain multiple aspects beyond the original scope. The analogy was also criticized for the lack of explanation of the finite radius of the strong interaction (which is mediated by gluons, which also have zero mass). However, this does not appear to be a valid criticism for the same reason already mentioned: not every analogy must necessarily explain more than expected. Acknowledging that the second part of the analogy is too far-reaching, and perhaps only useful in a different area from the didactic one of the blog, as it addresses the overly complex concept of high-energy electroweak interaction unification, let's focus on its first part.
We can first assume that our listeners are familiar with the target and that there is a fair relevance of common characteristics (emission of particles of different masses), which are not, however, numerous or varied. The phenomenology (intensity of the smell/intensity of interaction) is instead a weak point of the analogy: it is only apparently traceable to the same behavior of the characteristics object of logical induction, since the smell actually comes from single molecules vaporized, not entire corpuscles. However, the analogy has good predictive power, and the target is economical. According to these criteria, the analogy in question turns out to be a reasonable and effective tool for explaining the concept under discussion.
A second example from which we can draw is the explanation of the so-called "naturalness" problem of the Higgs boson mass. The mass of the Higgs boson receives quantum corrections due to diagrams containing loops of virtual particles. These corrections depend on a cutoff parameter: it is the maximum energy value of the virtual particles that circulate in these loops. If we assume that the cutoff is an enormous energy corresponding to the Planck mass (MPl), these corrections are gigantic; this fact has led some theoretical physicists to speculate that new physics exists at a much lower scale than MPl, which provides a corresponding smaller cutoff, making the coincidence (the mutual cancellation of these huge numbers). The problem has been explained by Michelangelo Mangano with an interesting analogy:
"Imagine asking ten friends to give you an irrational real number between -1 and +1. Add up the ten numbers thus collected, and discover that the result is different from zero only to the thirtieth decimal place (0.000000000000000000000000000001). What do you conclude? Do you consider it a coincidence, or do you take it as evidence that your friends agreed?"
If we examine this analogy carefully, we realize that its deductive power is not clear. What do we know about the target that we don't know in the source? The small probability that the sum of large numbers gives a small number is not a concept that requires an analogy to be absorbed. The listener is certainly able to consider the ten-number game, but that system has nothing in common with the quantum corrections to the Higgs boson mass, which are easier to understand in the target than in the source. Additionally, using a range from -1 to +1 is perhaps elegant, but it distances from the idea of the enormity of the MPl cutoff, which is an important characteristic of the source.
We can improve Mangano's analogy by constructing a target system with the size of the ten numbers as a parameter: from the smallness of their sum, we can deduce the size of the parameter and the need for a cutoff. We are then led to propose a text like the following:
"Let's imagine that a friend plays the roulette game, and places bets on red ten times. The amount of the bet is decided absolutely randomly (for example, by generating a random number with a computer), but lower than a certain maximum limit M by default:
Bet amount = MR, (with R between 0 and 1). After ten rounds, the friend ends up with a profit of one euro. What can we deduce about the maximum M that he had set for each round? Would we think that M = 1000 billion euros? No! We are obviously led to believe that the maximum M was just a few euros!"
This version is better than the original one seen above because it allows us to understand more quickly how theoretical physicists deduce that there must be a cutoff, new physics at an energy scale not too high. The focal point of the analogy is not so much in the paradox of the cancellation of large numbers, which is also apparent in the source, but in the logical inference that is possible to operate on M.
Let's now consider the improved version of Mangano's analogy and analyze it critically according to the parameters discussed previously. First of all, the target is certainly familiar to our listeners. Additionally, the features object of the deduction (large numbers) are relevant to the inference (their mutual cancellation). This is not a very forceful analogy: the number of common characteristics between the two source and target systems is very small. The phenomenology, a crucial point, is coincident: the deduction that M (the scale of new physics, or the maximum bet) cannot be large focuses on the coincident phenomenological basis, here simple arithmetic, or if you want, even a Bayesian inference. As for the deductive power, it is certainly present and strong; however, the analogy is not very economical, as we have to call into question a particular method to calculate our bets. Overall, it is an excellent analogy, capable of helping people understand immediately a rather elusive concept: the deduction that new physics must be around the corner. It's also worth noting that the source system is extremely complicated to explain, while the target is simple and potentially familiar to listeners.
In 2012, I presented to the readers of my blog the considerations on the use of the two analogies seen above to explain the problem of naturalness. An interesting online discussion ensued, during which a reader proposed the following improvement to the proposed versions of the analogy in question:
"Suppose the sum of profits and losses of ten companies is equal to ten euros. Knowing only this, and assuming that the profits and losses are more or less equally probable, what size can we estimate for the proceeds of each company? One might expect typical lemonade stand profits! Instead, we would be very surprised if they told us that these companies have revenues in the billions of euros each, as it would be very unlikely to obtain a sum equal to such a small number like 10 euros. Therefore, we would doubt anyone who put together the list very carefully of companies to purposely obtain a total profit so close to zero. Similarly, physicists suspect that the unnatural, almost perfect balance of quantum corrections to the mass of the Higgs boson is due to a hidden structure that we have not yet discovered."
The advantage of this version over the previous ones is clear: as well as presenting a situation more familiar than a "random bet" or a collection of irrational numbers, the analogy of the budget of a company, with profits and losses, is also very simple and direct. The creation of this analogy demonstrates the effectiveness of the review process and self-evaluation of the pros and cons of proposed texts.
Finally, let's consider the attempt to explain the behavior of quarks and gluons in the proton using an analogy with the extension of a spring. It must be acknowledged that this analogy is a natural temptation for a physicist: the interaction potential of the strong force increases with inter-quark distance, akin to the potential energy of a spring. However, the analogy is only partial. Unlike a spring, which deforms if extended too far but does not break, and where the extremes are not essential parts of the system, the behavior of quarks and gluons in a proton is more complex. Without a clear understanding of the appropriate level at which to apply the analogy, the listener may become confused.
Given the limitations of the spontaneous analogy between a spring and the strong interaction string, the crucial question arises: what do we want the listener to understand? Clearly, we aim to convey the notion that quarks are confined within hadrons by the strong force and to explain intuitively why this is the case. Focusing on our goal, it becomes evident that a well-conceived graph (see figure below) can be a much more effective tool for explaining the details of quark behavior. Indeed, graphical visualization of physical phenomena often proves to be a preferable alternative to simple description and analog comparison. With carefully designed graphs and thorough explanations of their contents, we can highlight the characteristics that need to be understood and seemingly explain complex concepts in a simple manner, without losing sight of the specifics of the physical system under consideration.
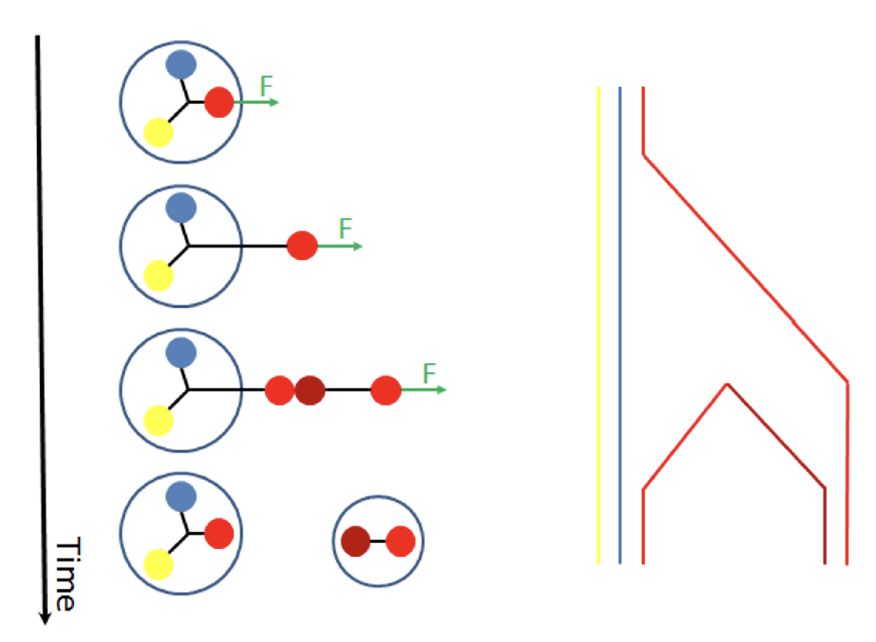
Figure 1. The attempt to extract a quark (red ball in the left graph) from a proton (composed of three quarks of different colors) by means of a force F leads to the stretching of the force line connecting the quarks together. As soon as the energy invested in the stretching becomes sufficient, it transforms into the mass of a new quark-antiquark pair (third diagram from the top). The new quark eventually returns to the proton to replace the one removed, and the remaining quark-antiquark pair stabilizes into a meson. The right graph schematically depicts the position of the quarks corresponding to the four configurations shown on the left; each colored line here represents the propagation in space-time of a quark.
In conclusion, this brief discussion underscores the role of analogy as an essential tool, though not the only one, in explaining physics. Its utility increases with the need for simplification, particularly when there is a significant gap between the level of preparation of the audience and the complexity of the concepts being conveyed. The pros and cons of an analogy must be carefully evaluated on a case-by-case basis, taking into account factors such as predictive power, audience familiarity with the target, and the correspondence between sources and targets. Engaging in self-evaluation of these and other characteristics of the analogies used in our teaching endeavors is a valuable exercise that I highly recommend.





Comments