But what is spin? Spin, for a macroscopic object, is connected to the rotation of a body around an axis passing through its center of gravity. For elementary particles, however, that description breaks down - how can you define a rotation for a point-like object? Still, that is a mysterious property of elementary particles, that behaves a lot like macroscopic spin, and makes all the difference: particles of half-integer spins make up matter, and ones of integer spins make up forces.
The W boson is a member of the family of integer-spin interaction carriers. It is a very heavy particle: its mass is as large as that of 86 protons; because of that, the interaction it mediates is very weak - it is indeed called "weak force". The weak force might be irrelevant to our lives, were it not for the fact that without it stars would not burn, and we would never have come to existence. So, let's pay some respect to the W boson!
The W particle was discovered in 1983 by a CERN experiment led by Carlo Rubbia, who was the first to realize that the most effective way to pull it off was to collide protons with antiprotons at an energy large enough that those particles could be created in sufficient numbers. He consequently led the effort that produced that result. He got a Nobel prize in physics for the discovery.
Nowadays, W bosons are still quite important for particle physics research. Their production in energetic collisions provided by the Large Hadron Collider signals that a weak interaction has taken place, something that is rare and indicative of interesting physics going on. But besides studying physical processes that produce W bosons, the LHC can study the W boson itself in great detail, too - for there's a lot we still do not know about this fascinating particle.
One of the things we would like to do is to catalog as precisely as possible the different ways that a W boson disintegrates, sizing up the relative probability of each. At a glance, the W is quite democratic in the way it decays: the simplest modes involve the production of a pair of fermions, provided that the process does not break any rule of quantum mechanics. Let me explain what I mean by "democratic" below.
The W can, e.g., decay into a pair of quarks; but since the W boson carries one unit of electric charge, the two quarks must collectively also carry that unit; so two up quarks would not work, as the up quark has a charge of +2/3 of an unit, and two up quarks would add up to a charge of +4/3, thus implying the creation of an extra 1/3 electric charge from nothing. Could it decay to an up -antiup pair ? Well, the anti-up quark has a charge of -2/3, so the total charge of an up-antiup pair is zero; again, this violates the rule of charge conservation. Instead, an up-antidown combination does the trick: the anti-down quark has a charge of +1/3, so +2/3+1/3=+1 and the W can, and indeed does, decay into an up-antidown pair.
Similarly, the W may decay to a charm-antistrange pair (charm has charge of +2/3, antistrange +1/3). Instead, the W cannot decay into a top-antibottom pair (which would be the third set of quarks we can pair up with the correct charge composition) because the top quark itself is more massive than the W boson: that decay would violate the conservation of energy.
W bosons can also decay into leptons, the other kind of half-integer spin matter particles. A possible combination is a positron-neutrino pair: the positron (the positive-charged version of the electron) has a +1 charge, and the neutrino has zero charge. Similarly, a muon-neutrino pair does the trick, and so do tauon-meutrino pairs.
If we add things up, we see that the W boson may decay in five different ways: up-antidown, charm-antistrange, and three leptonic modes. However, the quark modes are actually three each, as quarks come in three different colours, so the W may produce a red-antired up-antidown pair, or a blue-antiblue up-antidown pair, or a green up-antidown pair, and these are distinct things in the quantum world; and similarly for the other quark mode. So the possible distinct decays are nine. Now, I said before that the W is democratic. That means it decays one ninth of the time into each of the above combination of fermions. Collectively, quark modes get 2/3 of the share, because of colour.
Things do not stop there, if we want to accurately study the physics of W boson decays. That's because when the W produces quarks, these particles cannot just fly away in opposite directions: they carry colour, and a unbreakable rule of quantum chromodynamics (the theory that specifies the dynamics of quarks and gluons, objects subjected to the strong colour force) states that colour cannot exist in observable particles. So those up and antidown quarks must somehow bind into colourless hadrons (that's the name given to particles subjected to the strong force, which indeed contain quarks in their interior).
Because of the above, it is possible that the W boson produces a quark pair and this quark pair just recombines into a single colourless hadron. The lightest of these particles is the pion (an up-antidown combination, indeed). But this process cannot happen alone: the two quarks are shot in opposite direction in the reference frame where the decaying W is sitting, so it does not make sense that a W decays into a single pion - this would not conserve momentum, another thing that is totally forbidden both by quantum mechanics and by newtonian mechanics in fact.
However, what is possible is that the W produces a up-antidown pair, and in addition, an energetic photon is emitted. The photon allows momentum conservation to check out, and the two quarks can merrily unite and form the pion. From the outside, what you will be allowed to see is only an energetic photon flying out in one direction, and a pion coming up in the opposite direction!
The W boson decay to a pion and a photon is a rare process, because it calls for the action of two distinct interactions: the weak decay, plus the electromagnetic photon emission. Theoretical calculations of the rate are affected by large uncertainties, so we do not really know how frequent the decay is. It could occur once per million W decays, or just once every billion. So it's quite interesting to try and measure it experimentally... But of course, we need loads of W bosons to pull this measurement off!
The CMS experiment at CERN recently produced a search in its large datasets of proton-proton collisions. While the result of the search is not the most precise to date, it is quite interesting for its use of W bosons produced in the decay of top quark pairs. Since top quark pairs are copiously produced and easy to collect by CMS, and each event yields two W bosons and two bottom quarks, one may select them based on those general characteristics, and then search for the signature of W to pion-gamma decay in the collected set.
The money plot that summarizes the search is shown below. It shows the reconstructed mass of pions and photons in top quark event candidates selected by CMS. A bump at 80 GeV would signal that some W bosons decay indeed to pion-photon pairs; but as this is a quite rare process, the dataset is dominated by backgrounds, and one can only place an upper limit on the process.
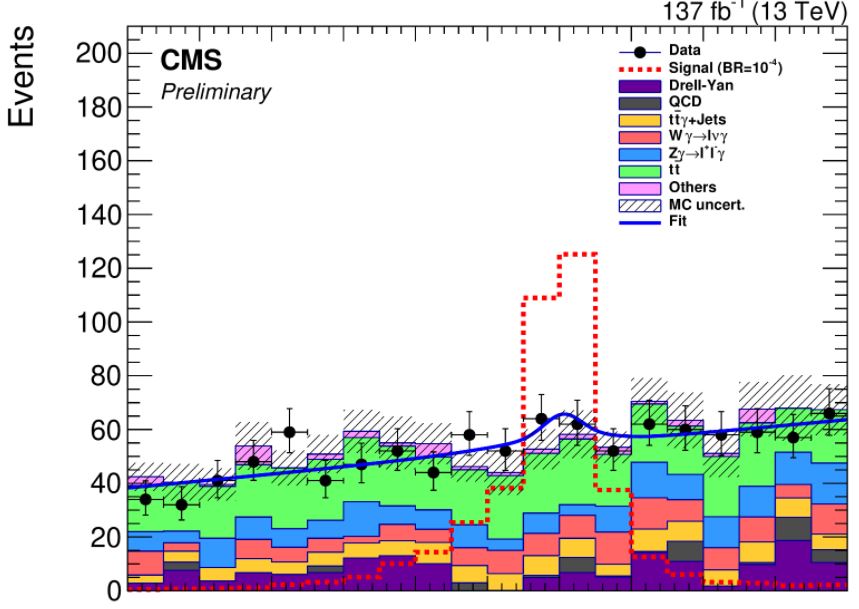
The small bump in the fitting curve overlaid to the histogram shows that CMS cannot rule out a small contribution from signal events in the data, and that translates into the upper limit on the decay probability: a part in hundred thousand. We are thus still far from the interesting region of rates, which may actually probe the predictions of different theoretical calculations; but we are getting closer with larger datasets. I fully expect that the LHC will ultimately see this process in the future!
---
Tommaso Dorigo (see his personal web page here) is an experimental particle physicist who works for the INFN at the University of Padova, and collaborates with the CMS experiment at the CERN LHC. He coordinates the European network AMVA4NewPhysics as well as research in accelerator-based physics for INFN-Padova, and is an editor of the journals Reviews in Physics and Physics Open. In 2016 Dorigo published the book “Anomaly! Collider physics and the quest for new phenomena at Fermilab”. You can get a copy of the book on Amazon, or contact him to get a free pdf copy if you have limited financial means.






Comments