J/Psi mesons
Let me begin with a very simple peak: the invariant mass of electroon pairs in the 3-GeV whereabouts. This plot contains the signal of J/Psi meson decays, of course. The J/Psi particle is a bound state of a charm and an anticharm quark, and this particle decays to electron pairs 6% of the time.
By itself, this is an important thing to note: particles composed of hadrons decay to leptons (electrons, muons, taus) with a significant rate only when there is something preventing the usually more frequent decay into lighter hadrons by strong interactions. In the case of the J/Psi, two things conspire: one, the mass of the J/Psi (3.097 GeV) is smaller than twice the mass of the lightest hadron containing charm, the D0 meson: this makes the decay J/Psi -> D0 anti-D0 impossible. Note that in such a reaction the two charm quarks would retain their identity: strong interactions cannot change the flavour of quarks.
But strong interactions might turn a charm-anticharm state into a non-charmed state if they managed to proceed through the annihilation of the charm with the anticharm of the J/Psi ! Indeed, the J/Psi has zero total "charmness", a quantum number which is +1 for charm quarks and -1 for anticharm quarks, and which for composite systems simply adds up. Let us see how that zero-charm-in-zero-charm-out strong reaction could proceed: the two charm quarks in the J/Psi get close together, annihilate, and produce gluons; the gluons then materialize into lighter hadrons.
Let us see if that is possible with one gluon. No, it is not possible! The J/Psi does not have a net colour charge, while a single gluon does. So the reaction violates the conservation of colour charge, and simply does not happen. Two gluons ? Well, two gluons may combine to have zero net colour charge, but there is then another quantum rule that prevents a J/Psi to turn into two gluons: the J/Psi is a vector particle -it has spin 1, and negative charge-conjugation quantum number- and so do the gluons. The conservation of C-parity of strong interactions prevents two gluons as a final state (and not, as I too quickly wrote here earlier in a failed attempt to trivialize, because a spin of 1 cannot be decomposed into two spin 1 particles, since this is not true).
The above may sound very weird to you, but you need not be bothered further by it. The result is important though: the J/Psi meson can decay through strong interactions only by emitting at least three gluons. And emitting three gluons means that the reaction pays the price of three strong-interaction vertices: this makes it much less frequent than it might be, and electromagnetic decays have a chance to steal some of the J/Psi mesons from their hadronic fate, producing instead pairs of electrons or muons. That is the reason why we were able to discover the J/Psi meson in 1974, and why we can see it clearly with cleanly identified electron-positron pairs even with a relatively small dataset with CMS today.
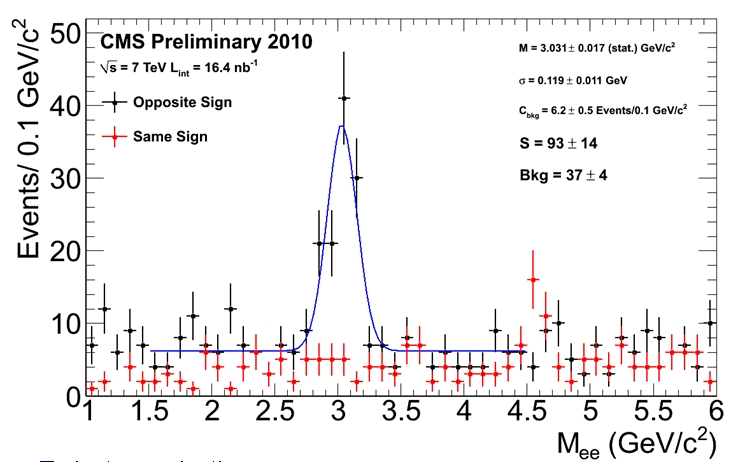
The figure above shows the invariant mass of electron pairs of opposite sign (black points) and same sign (red points). Of course, same-sign electron pairs are accidental backgrounds (due to other processes which need not concern us here). The opposite-sign distribution instead evidences a tall peak of J/Psi mesons, as expected. A blue line fits well the excess to the J/Psi hypothesis, and reveals a signal of 93 candidates on top of a background of 37.
W bosons!
The first W boson signals at the LHC have been shown two months ago in event-displays by ATLAS and CMS. However, seeing the collective behavior of the decays of these particles in histograms of the most tale-telling kinematical variables is a totally different matter!
W bosons are identified easily when they decay to muon-neutrino or electron-neutrino pairs. This happens about 11% of the times for each channel: the W always decays by weak interactions, and weak interactions share evenly the final state among the possible fermion-antifermion pairs that W bosons produce. The only constraint, of course, is that the final state has a total electric charge of one unit!
So for a W+ particle we have the chance to produce a antielectron-neutrino pair, or a antimuon-neutrino pair, or a antitau-neutrino pair. Fine. But also quark pairs can be produced: a up-antidown pair, or a charm-antistrange quark. Top-antibottom pairs instead are prevented by the fact that the top quark is twice as heavy as the W boson, so that reaction would violate energy conservation!
Let us take stock: three lepton categories, two quark categories. But quarks count for three each!!! In fact, quarks have colour charge, and there are thus three kinds of each. Weak interactions are extremely democratic, so each quark pair counts for three. So three leptons, 2x3=6 quark pairs... Nine possible final states. Therefore, each final state gets a 11% chance! Easy, is it not ?
The distribution below shows the transverse mass of electron-neutrino pairs identified by CMS in its early 7-TeV dataset. The transverse mass is computed by ignoring the component of motion of the electron and neutrino along the beam axis: only two-dimensional momentum vectors are used. The reason is that, while for the electron the z-component is well-measured, for neutrinos it is not measured at all. The neutrino momentum is in fact determined by the imbalance in the plane transverse to the beam direction of the total momentum of particles produced in the collision. The component of the neutrino momentum in the beam direction is impossible to measure, because we do not measure all the particles that escape along the beams...
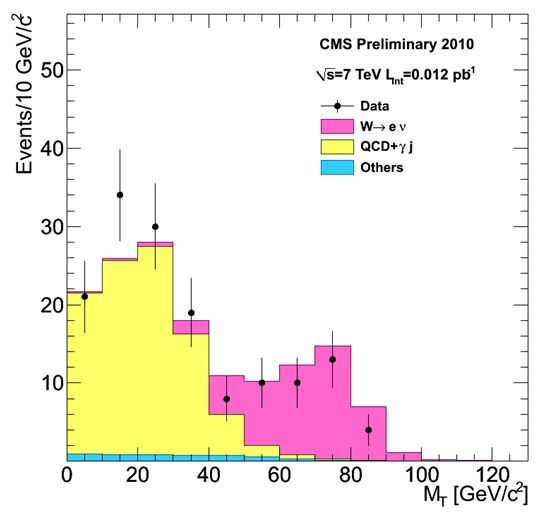
Transverse mass has a funny shape: it is not a normal Gaussian-like peak, rather it is a peak with a long high tail on the left. Still, it is a quite distinguishing feature! So you can see the data (black points) compared with predictions of the simulations: the pink histogram is the contribution expected from W boson decays. There is a very good match. Note the yellow contribution from "QCD" backgrounds: these are in part events with a photon faking the electron signal, and in part events where the electron is in reality a hadronic jet, and the signal of missing energy is due to a mismeasurement. The contamination can be easily removed by improving the purity of the selection.
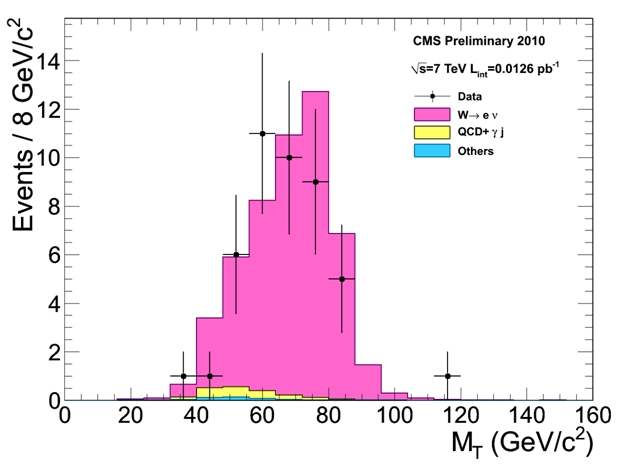
And in fact, even better is to see what happens if one applies those basic selection cuts, to improve the purity. The figure below shows that CMS can easily detect W decays with very small backgrounds!
Z bosons
Finally, Z bosons. Z boson decays to electron-positron pairs are ten times less frequent than W decays to electron-neutrino pairs, because of two things. One is that the cross section of W production is three times larger than that of the Z; the other is that the Z much prefers to decay to quarks than to leptons -a result of the electroweak interaction which I cannot explain here in detail.
So we see fewer Z decays than W decays, but still, when we find an electron-positron pair with a invariant mass close to 90 GeV, we are almost certain that it is a genuine Z decay, because there are very few backgrounds capable of producing pairs of electrons (real or fake) with such energy.
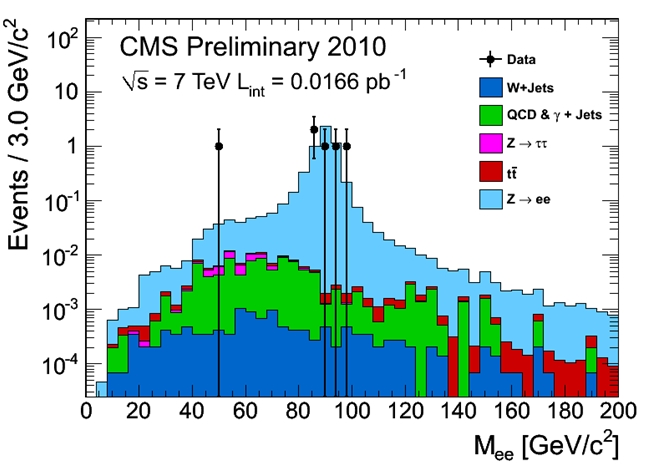
In the figure you see five Z candidates (black points) clustering around the nominal Z mass. A further event with smaller mass may still be a genuine off-shell Z decay, but let us forget about it. What matters is that Z bosons are there, and backgrounds (shown in dark blue, green, red, and purple) are small!




Comments