One of the three new resonances is likely to be the same as a particle already identified for the first time by the competitor LHCb experiment, while the other two are new finds. LHCb is also a LHC detector, but it is one optimized for heavy hadron spectroscopy; while CMS is a "general purpose" detector built with the primary goal of finding the Higgs boson (a 2012 success) and searching for new phenomena at the highest-energy frontier.

[Above: the CMS detector in an open configuration for servicing]
Before I show you the data and discuss the results of CMS, I wish to try and explain the multitude of things that are given for granted in the above two paragraphs. So, what is a resonance? What is a hadron? And what the heck is a J/Psi meson? Worry not, you are about to find out.
Resonances
Resonance is a very common phenomenon in physics, and one which occurs at all length scales. There are resonance orbits of bodies in the solar systems, resonance phenomena in musical instruments, and resonant frequencies in molecules. In all cases, what happens is that an oscillatory motion of a system can be amplified if stimulated at special frequencies (the natural frequencies of the system).
What happens is that a resonating system can store energy in two different ways - as kinetic and potential energy; the transfer of one form of energy to the other occurs without loss (damping) when the system is subjected to an oscillating force that has frequency close to its natural frequency of oscillation. This results in an amplification of the resulting oscillation.
You can easily observe this phenomenon when you hit a low-pitch note on a piano and all chords are left free to vibrate (by pressing the pedal on the right side), this produces an amplified vibration in other chords that have natural vibration frequency equal to multiples of the chord you hit. But similarly, you can observe that your voice sounds much louder when you sing at specific frequencies inside a shower enclosure. Or you can try tapping your glass of water and see if you do it at the right frequency, when the water will suddenly "shoot up".
In particle physics, the term "resonance" indicates something slightly different, though. In this article we talk of hadron resonances, which are particles composed of quarks and antiquarks. These systems have a mass which is contributed by the oscillation energy of their components. A quark-antiquark pair, e.g., will have the components jiggle around one another at a specific frequency, and this provides the composite system with kinetic energy. The system is unstable and liable to decay - in some cases in a mindbogglingly short time - when the total energy is released in the form of two or more decay products.
The shorter the lifetime of the resonant state is, the more "uncertain" is the vibration energy, and hence the energy of the decay products. By studying the energy distribution of the latter we can infer how long lasted the original resonance: the shorter the lifetime, the larger the spread of energies we observe. This way, we have access to precisely measure the lifetime of particles that live a time so short that light cannot even traverse an atomic nucleus in the meantime.
The resonances observed by CMS were discovered by identifying and measuring with precision the decay products they yielded in their disintegration. In all three cases, these were two J/Psi mesons. And what are these?
J/Psi mesons
The J/Psi is a very special particle, for at least a couple of reasons. Their simultaneous discovery by two US laboratories in November 1974 granted a small shower of Nobel prizes because of its importance. In fact, its observation proved that they, as well as a host of other particles previously discovered, were made of quarks.
Such a paradigm-changing realization occurred basically overnight, also thanks to the earlier work by several theorists who had predicted that one special kind of quark, the charm, had to exist, and be massive enough to make another particle decay exceedingly rarely in a way that would otherwise have to be observed copiously. This was the so-called "Glashow-Iliopolous-Maiani mechanism", by the way. The J/psi, weighting twice as much as the charm quark, was immediately recognized as a composite hadron made of a charm and an anticharm quark. A resonance itself!
J/Psi mesons are copiously produced in LHC proton-proton collisions, and they are very cleanly identified because they decay, a few percent of the time, into a pair of muons - and muons are very easy to detect and measure precisely. Nowadays we exploit the dimuon decay of J/Psi mesons as a very clean way to study particles that themselves decay into J/Psi mesons. We just have to "wait" for the produced J/Psi to yield muon pairs, and measure those. Saying we wait for the J/Psi to decay is a bit of a joke, as the decay is instantaneous for all practical purposes - it takes a few billionths of a billionth of a second to take place.
The CMS result
CMS looked for _pairs_ of J/Psi signals in their data, by sorting out events that contained four muons and verifying that the two opposite-charge pairs each had a total energy corresponding to the mass of the J/Psi meson, 3.097 GeV. If you perform such a selection the resulting data sample is very pure, as muons are rare objects to begin with, and they are identified with very little background by the CMS detector. Further, the J/Psi resonance is quite narrow, and the energy resolution of muons is very good: hence, if you measure two muons with a total mass of, say, 2.8, or 3.3 GeV, you are certain that they are _not_ due to a J/Psi decay, but something else. Only those pairs whose mass piles up at 3.1 GeV are those you care about.
Once you have pairs of J/Psi mesons beautifully reconstructed into muon pairs, you can again ask the question - what is their combined energy in their rest system, or to be precise, their invariant mass? That corresponds to the mass of the object that decayed into the pair. Note, though, that in general you should not assume that if you have seen two J/Psi mesons there has to have been a heavier particle that decayed into them: in fact, the opposite is true, until you can prove that indeed, in some of the cases that's exactly what happened.
How, then, can you prove that a heavy resonance was produced and then decayed into the two J/Psi mesons? Well, if the two J/Psi mesons "resonate" at a very specific mass value, that kills it. What you look for is again a peak in the invariant mass distribution - this time, of the two J/Psi mesons. The invariant mass distribution obtained by CMS this way is shown below.
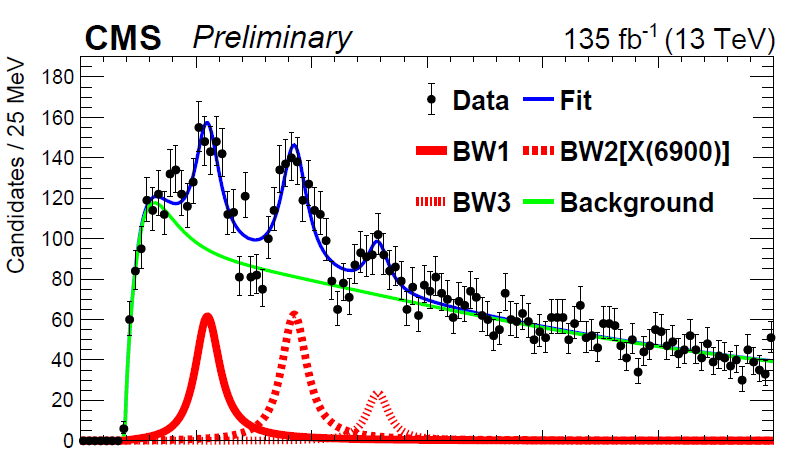
As you can see, the data in the histogram (black points with vertical uncertainty bars) can be well interpreted by a "continuum" - a smoothly falling mass distribution, in green - on top of which lay three distinct peaks (in blue, whose shapes are also reported in red). The peaks are the signature of the three discovered resonances.
To be precise, CMS cannot claim with confidence that all three peaks are new hadrons: the third one is not significant enough, although by a small margin. The significance of a peak in a distribution like the one above is computed by a statistical procedure that asks the question "what is the probability to observe data that departs at least as much as these from the background-only hypothesis, if the data is indeed only composed of background?", for each of the three resonances in turn. In other words, the procedure quantifies the probability of a background fluctuation similar or more striking than the one seen. The probability is then converted in a significance with a simple formula involving the integral of a Gaussian distribution.
In the case of the peak on the right, the significance is barely below five standard deviations, so its confermation will have to wait some more data or some other experiment. But the other two peaks are definitely worth an observation claim of new resonances.
Finally, you could well ask - what is the _practical_ significance of this find? What do we know now we did not know before CMS pulled this result off? Well, the answer to this question is not a one liner. I need to explain that the physics of bound states of quarks and gluons is very complex, and we have not understood it in full detail yet. We are still in a stage when we compile catalogs of all the discovered states and their properties; in some cases we are able to explain these properties precisely, but in others we still aren't.
So the new CMS discovery is a small step in the direction of shedding light on this incredibly complex menagerie of composite particles. Maybe, the day we understand every detail of these systems, we will be able to exploit that knowledge in ways we have no clue about today. Or maybe we will only be able to pat ourselves on the back - as finding a small truth is more important that to ponder at length of the biggest questions without reaching any conclusions, as Galileo Galilei famously pointed out four hundred years ago.
---
Tommaso Dorigo (see his personal web page here) is an experimental particle physicist who works for the INFN and the University of Padova, and collaborates with the CMS experiment at the CERN LHC. He coordinates the MODE Collaboration, a group of physicists and computer scientists from eight institutions in Europe and the US who aim to enable end-to-end optimization of detector design with differentiable programming. Dorigo is an editor of the journals Reviews in Physics and Physics Open. In 2016 Dorigo published the book "Anomaly! Collider Physics and the Quest for New Phenomena at Fermilab", an insider view of the sociology of big particle physics experiments. You can get a copy of the book on Amazon, or contact him to get a free pdf copy if you have limited financial means.






Comments