The discovery of a new exotic hadron, named T_cc+,  was announced by the LHCb Collaboration a little over a week ago. Unlike some previous discoveries of other resonances by the LHC experiments (dozens have been announced since 2010 by LHCb, and to a lesser extent by CMS and ATLAS) the one of the T_cc+ is is very significant and exciting, and it promises to advance our understanding of low-energy QCD, with repercussions across the board.


In this article I will try to explain what makes it significant. For that, I will be leveraging explanations and input from my dear friend Marek Karliner, who is a world-class expert in the physics of heavy hadrons, and who correctly predicted the mass of the T_cc+ in 2017 with Jonathan Rosner; of course, any mistakes in the text below are only my fault.




Exotic hadrons, what are they?




Simply put, exotic hadrons are particles constructed by non-standard combinations of quarks, where "standard" means ones that you can put together as quark or antiquark triplets [e.g., the proton (uud) or the antineutron (anti-u anti-d anti-d)] or quark-antiquark pairs [e.g., the three pion states pi+ (u anti-d), pi0 (u anti-u), pi- (d anti-u)].


Triplets are called "baryons", and quark-antiquark pairs are called "mesons". To constitute a valid bid for an exotic hadron, however, the particle you make up must live long enough to be identifiable as a bound state, if even for a very short instant.


You can of course imagine to bring together two up quarks, for instance, and claim you built an exotic hadron, but your attempt would fail as  quark pairs possess a color charge, and anything that has a color charge cannot be a bound state. So, the trick is to create quark combinations which have a zero net color charge. You can do this with three quarks because the combination red-green-blue is colorless, and you can do this with quark-antiquark pairs because a red-antired combination is again colorless. With two quarks, the trick does not work.


The question of whether exotic hadrons exist came to the forefront of particle physics research a bit over fifty years ago, when the quark model had not been yet proven: quarks were considered an interesting mathematical concoction, but one devoid of objective existence. Back then, theorists were looking for extensions of the basic scheme put forth by Murray Gell-Mann and George Zweig in 1964, who had proposed that all hadrons until then discovered could be explained by combining up, down, strange quarks and their antiquark analogs.  


I should mention that in their seminal papers both Gell-Mann and Zweig did suggest that by adding a quark-antiquark pair to a baryon or a meson you might still be able to create "stable" 5- or 4-quark systems - where stable is supposed to mean "whose constituents keep orbiting around each other for more than a few rounds" before anyway decaying to lighter particles; but the question whether  these exotic states actually exists remained unanswered for a long time.


All the while, new particles where sought in fixed-target collisions of beams of protons, pions, kaons, or even neutrinos, and the reconstruction of the collisions made use of tracks of droplets left by charged particles that ionized a supersaturated liquid in so-called "bubble chambers". But as quarks became established as real entities, with the "November revolution" of 1974, the question became a bit less compelling.


(In November of 1974, two American experiments at SLAC and Brookhaven independently and jointly announced the discovery of a particle, thereafter called "J/psi", which screamed to be interpreted as the bound state of a charm-anticharm quark pair. In a single swoop, this proved that quarks were real, and that there were at least four of them).




LHCb, the game changer




After a few imaginative, controversial claims, which remained undecided of exotic hadrons consisting of only light quarks (u, d, s) and were eventually retracted, the real interest on tetraquarks (mesons plus a quark-antiquark pair) and pentaquarks (baryons with a quark-antiquark add-on) was revived when the Belle experiment at the KEK accelerator in Japan discovered an usually long-lived resonance, subsequently named X(3872). Its properties are such that that it clearly contains a (c cbar), i.e. a charmed and an anticharmed heavy quark pair. Its other properties are best understood by assuming it also contains a light quark-antiquark pair (u ubar). Remarkably, its mass is almost exactly equal to the sum of masses of two mesons, one containing a (c ubar) and the other (cbar u).


X(3872) was the first uncontroversially exotic hadron discovered.  Today we understand that it is the presence of a heavy quark-antiquark  pair which provides the necessary stabilizing factor and makes its existence possible.  More on this later.


X(3872) is electrically neutral, so its exotic nature as a four quark state is not immediately obvious. A few years after the discovery of X(3872) the Belle and BESIII experiments in China discovered closely related long-lived resonances now known as Zc and Zb, which decay into a (c cbar) or (b bbar) pair and a charged pion. These states {\em must} contain at least 4 quarks. We say that they are manifestly exotic.


In parallel, the LHC accelerator started to produce large datasets of proton-proton collisions, and its "Heavy-flavour-physics-focused" LHCb experiment started to observe with large statistics several resonant states containing heavy charm and anticharm which could indeed be interpreted as being composed by four or five objects. 


Now, the real question in this very interesting branch of particle physics, after the handful of new tentatively-exotic hadrons became a small menagerie, is whether they are better describable as loosely bound states of a baryon and a meson (for pentaquarks) or two mesons (for tetraquarks), or whether the quarks making these states up really jiggle around one another without any real belonging to two- and three-particle systems. In other words, can we think of these systems as a molecule made up by two bags of color-singlet clusters of quarks, weakly attracted by one another, which dance around one another for a little, and then dissociate, or should we instead think of them as a single fat bag of many quarks tightly packed in a confined space?


On that question the jury is still out as far as most of the so-far-discovered exotic candidate states are concerned. Yet it is a very relevant question if you consider the big picture: as long as 4- and 5-quark systems can be described by the "molecular" picture, there are, strictly speaking, no exotic color configurations of quarks: everything can be described by standard quark-model objects. On the other hand, if we really have to accept that these new particles are bags of four or five tightly bound quarks and antiquarks, then the picture really changes.




And last week, things changed abruptly.




When the discovery of a new T_cc+ particle, and its interpretation as a composite of two charm quarks and two light antiquarks, was announced by LHCb at the EPS conference, it obviously made headlines - a new exotic hadron! But the significance of T_cc+ extends far beyond that of enriching the menagerie by one unit, and the reason is that it conclusively proves that exotic hadrons do exist, even in the strict sense. To explain why, I will give you below some background information. But first let us peek at the LHCb result.


The graph below shows the invariant mass of final states including a reconstructed D0 (a charm anti-up meson) and a D*+ (a spin-1 charm anti-down meson) particle, identified by the experiment in Run 2 LHC proton-proton collision data. As you can clearly see, there is an unmistakable
"threshold peak" sitting at a mass of 3875 MeV. A resonance! Indeed, what the piling up of those events at that specific mass value means, is that D0 and D*+ particles seem to have been "resonating" in a composite system before being released as individual entities.






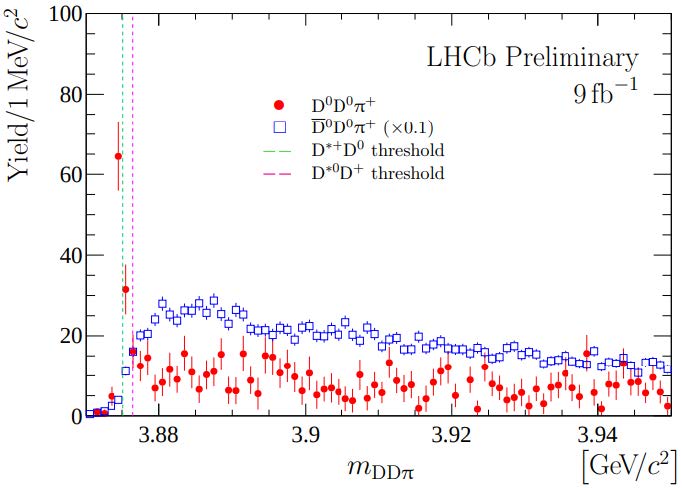
[Above, the distribution of reconstructed masses of DDπ systems (in red) is compared to the scaled-down shape of the distribution for anti-D0-D0-pion systems (in blue), which do not show a resonant structure at threshold.]


And now, let's analyze the situation, starting with some generic background first.




The interest of heavy hadron systems




Why concentrating on heavy flavored hadrons? The answer to this question is twofold, and both parts involve a measure of pragmatism. The theoretically-motivated answer is that hadrons that contain one or more bottom or charm quarks can better be understood by phenomenological techniques that work around the non-calculability of quantum chromodynamics (QCD).


QCD is a wonderful theory, and we understand it pretty well - we can, e.g., write down the Lagrangian density for a system of quarks and gluons; but we cannot use it to compute physical quantities when the energy of the involved reactions is too small, because the QCD "coupling constant", alpha_s, is too large; alpha_s is in fact not constant, and it becomes small enough to allow QCD calculations only when reactions are very energetic.


The QCD force works by the exchange of gluons, and the coupling constant that describes those processes enters any calculation that involves the absorption of a gluon by a quark or the interaction between two or more gluons, as each of these basic processes takes place with an intensity proportional, through different coefficients, to alpha_s. And when you consider all possible gluon exchanges (there's an infinity of them, for any QCD process you think of), and the energy of the considered reaction is not high enough, the global result is a diverging series in powers of alpha_s. Darn it, we cannot get any meaningful result out of it!


In a nutshell what I am trying to say is that if you want to know, e.g., the QCD contribution to the energy of a system made of a quark and an antiquark orbiting around one another, you may start by considering interactions of the pair which involve the exchange of one gluon. This is the "leading-order" contribution to the binding of the system. The result of your calculation will then be proportional to the QCD coupling constant alpha_s.


Once you're done calculating this, you then say "OK, let us now consider sub-leading corrections to this result" - so you turn to interactions involving two gluons. There are several of these (gluons come in eight different kinds, and there's a number of ways two-gluon exchanges may
take place), so this keeps you busy for a while. Once you're done, you realize that in all considered cases the result depends on the square of the QCD coupling constant. Because alpha_s is large, this "sub-leading" correction ends up being too large for your original leading-order result to be considered a valid approximation - it was simply way off.


You are thus bound to check whether processes involving three gluons also provide large variations of the result. And they do, because they are proportional to the cube of alpha_s. And the pattern repeats if you add more gluons. By considering more and more ways through which two quarks can interact you would hope that you get a better and better representation of the physics, but this is not the case. In other words, you are looking at a non-converging, useless series of an infinity of terms.


Heavy quarks in the system do not radically alter the above frustrating situation (the values of alpha_s are smaller as the heavy quarks have larger mass, but not enough to make series converge), but they provide handles for alternative calculations. E.g., if one of the two objects is heavy with respect to the other, the dynamics become simpler, because you go from a situation where two quarks both affect one another significantly to one where the heavy quark sits in the center of mass and the light one jiggles around it - as in planetary systems, following the motion and the energy states of the lighter member of a pair of objects is an attractive simplification and a valid approximation!


In addition, one may use old-fashioned tools that work by extracting useful information from the mass of hadrons that differ by the exchange of a quark for another. These allow to derive useful formulas and to make predictions for new states; the predictions become more and more
accurate if the systems include heavy quarks, because the systems are increasingly non-relativistic: that's because heavy quarks move slower inside hadrons, so the total energy of the system can be better understood as the simple-minded sum of the masses of the components. 


An analogy of these methods would be your weighting yourself as you have your dog in your arms, and then weighting yourself after putting the dog down and picking up the cat. The two results tell you what is the mass of the dog minus the mass of the cat, so now if you know what's the weight of a bag containing three cats, you also know what is the weight of a bag containing two cats and a dog. My god, I can usually come up with better analogies - apologies for this one.


So, heavy quarks help us as they provide means to gain insight into complex multi-quark systems. But as I mentioned above there is another reason, of more experimental flavor, why studies of exotic hadrons focus on systems that include heavy quarks. It so happens that it would be harder for multi-quark systems made of light quarks to make up states which end up being stable for the strong interaction: the democratic arrangement of quarks of similar masses in a multi-quark system readily creates situations where there is a substantial probability for quark-antiquark pairs to overlap spatially - which means there is a very large probability for the annihilation of the pair or the dissociation of the pair from the rest of the hadron by a strong-interaction-mediated decay. 


When there are heavy quarks in the mix, the binding energy of those heavy things makes the total mass of the system small enough that there is not enough energy for the system to dissociate by strong interactions. Hence, while exotic hadrons made of light quarks have very small lifetimes, and thus very large "natural widths", exotics made with heavy quarks can be long-lived with respect to QCD, and produce narrow, well distinguishable resonances. In practice, low-mass exotic hadrons may exist but they are hard to observe as well-defined resonances, as their mass is ill-defined: like a very low-tone piano string hit very lightly, their exact pitch is uncertain, because they "vibrated" for too few periods before extinguishing.




More on the T_cc+




Unlike previously discovered tetraquark and pentaquark states with two (or more) heavy quarks, the T_cc+ contains a surplus of two charm quarks, instead of an equal balance of charm-anticharm pair(s). When you put a charm and an anticharm close together, nothing can prevent them from
binding into a charmonium state, making the four-quark system decay into charmonium plus meson(s). But when you take two charm quarks close together, they happily jiggle around without even thinking of mating - they are arranged in a colour anti-triplet, and QCD forbids colour anti-triplets from existing as separate hadron, separate from other quarks.


Now, a crucial fact is that the charm-charm potential is non-relativistic, and it can be approximated by a Coulomb-like form at short distance, and a linearly growing function at large distance. Thus at short distance the strength of the interaction scales with 1/r.  At the distance of about one fifth of a Fermi, this means hundreds of MeV.


From what I mentioned above, you well realize that a relevant question is how much binding energy the pair generates - this is "negative energy" that gets subtracted from the sum of the quark masses in determining the total mass of the multiquark system. If enough energy is subtracted, the system cannot decay by strong or electromagnetic interactions, as the sum of masses of any pair or set of particles containing the original heavy quarks are all higher than the mass of the exotic state. This makes the system long-lived -it can only decay by flavor-changing weak interactions-, and more readily interpreted as a strongly bound state, which as I explained above makes things qualitatively different.


Now, according to the 2017 prediction of Karliner and Rosner (now perfectly-well verified by experimental observation), systems that contain two charm quarks stabilize at a larger distance than ones with two bottom quarks, which were also studied in their work. For the now discovered T_cc+ hadron, the attraction is big but not big enough, and the two charm quarks "sit at the threshold". In other words, the binding energy is not large enough to completely rule out a strong decay, which does take place, albeit with a very small natural width (about 0.5 MeV).


In their 2017 paper Rosner and Karliner, using the quark model as a basis for their calculations, predicted that the doubly charmed T_cc+  hadron would behave as now observed. Just  6 days later two other very distinguished theorists, Quigg and Eichten, addressed the same problem with a different technology, leveraging heavy quark symmetry arguments. They predicted that the T_cc+ would have a mass 102 MeV above the "open-charm" strong decay threshold. Later another eminent player in the theory of heavy quarks, Eric Braaten, improved on Quigg's and Eichten's calculation because the latter did not give uncertainty bars, and he came up with the estimate of 72+-11 MeV above threshold.


Summing that up, we see that something non trivial is going on, because heavy-quark-symmetry-based calculations are supposed to be very solid, and there is no doubt on the correctness of the calculations produced by those theorists. It is important because HQ symmetry is very extensively used nowadays to compute predictions for processes beyond the standard model, which we actively search in LHC data. If there is a loophole in those calculations it should be plugged as soon as possible!


Another thing is also clear. All theorists, from Karliner and Rosner to  Quigg and Eichten, agreed in 2017 that T_bb, four-quark states with double bottom must be deeply below the threshold at which they may decay by strong interactions. Later with lattice QCD calculations (another tool that takes the problem from a very different angle, involving quantum-mechanical calculations on a discrete space-time lattice and extrapolation at zero lattice spacing) it was also agreed that double bottom tetraquarks cannot decay by QCD processes.


It is important that the theorists' consensus converged for those particles, and that it diverges on the T_cc+. Now, the measurement of the mass of the T_cc+ found by LHCb is of 3875 MeV, with a very small uncertainty, and Rosner and Karliner predicted it to weigh 3882+-12 MeV. This verified prediction is a definite milestone in the road of unraveling the mystery of heavy exotic hadrons. For the first time we have insight, and robust predictions, of a third class of stable hadrons which contain more than a 2 or 3 quarks combination!




Molecules and bags




Earlier I mentioned that for previously discovered "exotic" hadrons there is no clear indication of a strongly bound state. Let me revisit that statement now that I (hopefully) have clarified what are the important ingredients of these studies.


If we look at other multiquark states, there is strong circumstantial evidence that e.g. the pentaquarks discovered by LHCb (four particles in total) are molecules, because their masses are very close to baryon-meson thresholds and because they decay to a J/psi (a charm-anticharm
bound state) and a proton, with a decay width of 20 MeV or less, while the phase space is a full 400 MeV: these particles, in other words, take a long time to decay given the large number of kinematic configurations that would be allowed (the more possibilities you have to generate momenta for the final state particles, the more readily a particle will decay - this is a rule we learned 80 years ago from none other than Enrico Fermi).


Put still differently, if you place all five quarks of those pentaquarks in one bag there is nothing to prevent the charm-anticharm system to hadronize in a J/Psi, so the fact that the decay is slow means that the  charm and the anticharm in the pentaquark must overcome some kind of an obstacle to get close to each other. The simplest explanation is that they live far apart.




More predictions




It is very interesting to look at the quantum numbers of the newly discovered state. The symmetry properties of a quantum system made of quarks results from the combination of four parts: a spatial part, a flavor part, a spin part, and a color part. We can then analyze the system one bit at a time, figuring out how the various parts of the wavefunction behave.  


We start with the two charm quarks in the T_cc+, which sit on top of each other: they must thus be in a spatially symmetric s-wave configuration. We are talking here of two fermions, which obey the Pauli exclusion principle. According to that, these particles can only sit next to each other if their wavefunctions are globally antisymmetric with respect to the operation that exchanges one with the other.


As far as color is concerned, they are in a state which must be a color antitriplet because of the rules of QCD. Then one can deduce that the charm-charm system must have spin 1, due to Pauli's principle. The two ½ spins of the charms are thus aligned in the same verse.


Once we figured out how the charm-charm pair behaves, we may turn to the two accompanying light antiquarks, and ask ourselves what are the symmetry properties of the T_cc+ with respect to flavor.  The anti-u and the anti-d quarks that accompany the two charms can create an isosinglet
or  an isovector, two different situations: the first is a state which has no partners, the second is a state of a set of three, whose other two elements differ in the flavor space and create a vector of three similar states.


Now, insight from the observation of charmed baryons help sort the above question out: we consider the Sigma_c and the Lambda_c particles [both baryons made up by a (udc) quark combination] for a clue.  These baryons have a mass difference of approximately 170 MeV, 
and the difference is essentially due of to the first being an isosinglet, while the second is an isotriplet. Note that the quark content of the baryons is the same of the T_cc+ if we omit the extra charm, so we can fruitfully study these two baryons to sort out the flavor symmetry of the T_cc+.


I will spare you the details, but it turns out that Lambda_c and Sigma_c differ essentially by having the first a spin 0 / isospin 0 configuration, and the latter spin 1 / isospin 1. The two antiquarks of the T_cc+ can then be understood as a state with spin 0, isospin 0; the total spin of the T_cc+ is then that of the two charms. We are thus looking at a spin-parity state 1^(+),  and it is an isosinglet. As you see, this chain of deductions brings us to predict a very important fact: the newly discovered state is a singleton, it does not come in a triplet of states. If LHCb were to find two other states with the same characteristics, all the theory we have constructed would be dead! But as far as I know, LHCb searches for such particles has indeed come up empty-handed...




And this down in the post, let's turn <rant mode on>...




After chanting the glory of this new discovery, I feel compelled by mentioning a self-generated blemish with which LHCb decided to stain their otherwise excellent scientific result. In their web site, LHCb nonchalantly states that the observed T_cc^+ peak has "a statistical significance exceeding 20 standard deviations". This is way off the scale of my "ridiculous-claims-o-meter", for reasons I explain (for the umpteenth time) below.


LHCb colleagues, ladies and gentlemen: there is no such thing as a "20 sigma significance". No, there really isn't. Even attaching "statistical" to the term you don't wash away the mark of absurdity from the statement. Saying that your peak is a 20-sigma excess means you know the background rate, as well as its probability distribution, with an impossible precision. Already a claim of 5-sigma or 6 is hard to defend, but we can usually get to reasonably explore the corresponding tiny p-values (of a part in 10 million or a few hundred millions). Going far above that, though, is nuts. The reason is that we simply cannot _prove_ that there be no effect capable of messing up the regular Poisson scaling of fluctuations, with the necessary precision.


Let us take that money plot again: the signal region (events with a reconstructed mass below 3.8765 GeV or so) contains about 110 events. What LHCb probably did, to cook up that "more than 20 sigma" estimate, was to compute the tail probability of estimated backgrounds (maybe uncertainty included, but then "statistical" would lose its meaning) fluctuating up to 110 or more events. I have no access to the original data, but I may imagine that their background was of the order of 10 events or so, maybe with a precision of plus or minus five events. Under a Gaussian approximation, a process with a mean of 10 events and a sigma of 5 indeed is twenty sigmas or so away from being able to generate an observed rate of 110 events. In simplified terms, 110-10 = 100 / 5 = 20 sigma. Of course, we know that this is an approximated calculation, as event rates are better described by a Poisson distribution, and for small event counts a Poisson is quite different from a Gaussian - I was being didactical there.


But now consider: what happens if the background distribution is not exactly a Poisson? Or if the uncertainty on the mean of the Poisson background is not perfectly Gaussian? These are usually irrelevant questions, but if you talk about the twenty-sigma tail of a Gaussian distribution they become an elephant in the room. Nobody can ensure that the probability distribution of some data or some uncertainty is known to that level of detail.


So pretty please, LHCb: stop talking about 20 sigma nonsense. You are a grown-up experiment, you need no longer prove you have it bigger than others!



---

Tommaso Dorigo (see his personal web page here) is an experimental particle physicist who works for the INFN and the University of Padova, and collaborates with the CMS experiment at the CERN LHC. He coordinates the MODE Collaboration, a group of physicists and computer scientists from eight institutions in Europe and the US who aim to enable end-to-end optimization of detector design with differentiable programming. Dorigo is an editor of the journals Reviews in Physics and Physics Open. In 2016 Dorigo published the book "Anomaly! Collider Physics and the Quest for New Phenomena at Fermilab", an insider view of the sociology of big particle physics experiments. You can get a copy of the book on Amazon, or contact him to get a free pdf copy if you have limited financial means.