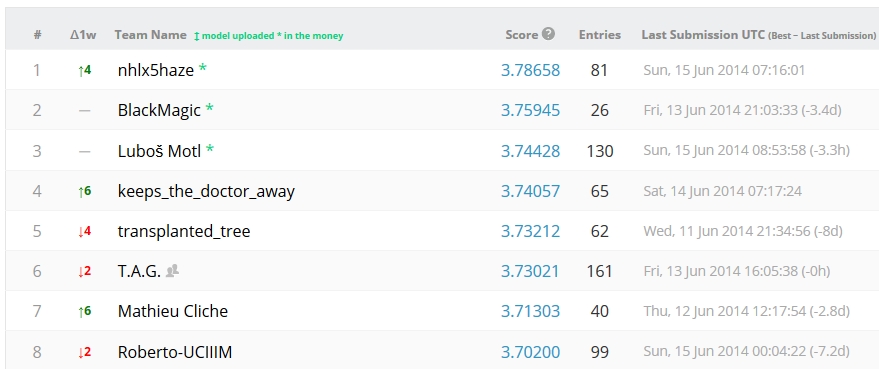
In the last few days, there has been a total revolution in the leading position, and a considerable increase in the best scores. And Lubos Motl is again third (and he would be first if there had been no movement in the other positions), implicitly answering some detractors who wrote comments in a previous post on the matter here. See the standings below.
"Ok, but why are you rooting for Motl ?," you might ask. After all, he has often been rather harsh with me, getting close to positions liable of a libel cause. My main guilt to him is to be a friend of Peter Woit, whom he perceives like the absolute evil, as Peter has been and is a critic of string theory. Plus, politically I belong to the left, while he is on rather reactionary positions. Further, I do believe that we are negatively affecting our climate with CO2 emissions, while he says it's baloney. Anyway, why am I supporting him ?
Well, first of all, I will always prefer an outsider with talent and good ideas to a big team with lots of resources and experience, and I have the impression that some of the leaders of the Higgs challenge belong to the latter category. But it would be nice to see Lubos giving a talk at CERN explaining to our ATLAS colleagues how to optimize their discriminating tools for complex multivariate searches.
One further question you might have is, "Doesn't a theorist winning a contest in categorization sound like a defeat for experimentalists?" After all, there are dozens of experimentalists also participating in the challenge, and they are those same physicists who analyze LHC data in search for new particles - is it not like saying that the LHC experiments are staffed with incompetent ignorants? No, that is not the case, and let me explain to you why.
Finding the Higgs in a background-ridden dataset does involve a performant selection of signal-like events. There are dozens of ways to perform such a selection, and some approaches are known to produce more promising discrimination levels than others. What one does with such tools is to take the initial dataset, which contains, say, 100 Higgs boson events immersed in 100000 background events, and work one's way to a super-selected sample where by discarding background-like events one remains with 20 Higgs events and 25 background ones.
A "counting experiment" may then allow the physicist to say "AHA: I expected 25+-5 events if the data were only made up by backgrounds, but I see 45: there is a significant excess due to what could be Higgs boson decays in the data!". The "background-only" hypothesis is very unlikely in such a circumstance, and we can speak of "evidence" for the Higgs signal contribution in our selected data.
It is important to realize that such a stringent selection as the one of the example above is based on believing that the kinematics of the signal and backgrounds conform exactly to those that are derived from simulation programs. Now, experimental physicists know that it is very dangerous to believe in these simulations to their last bit: in the past forty years dozens of spurious signals have been observed in super-selected data, obtained by relying too much on the tails of the distribution of this or that kinematical variable. See the graph below to understand what I exactly mean.
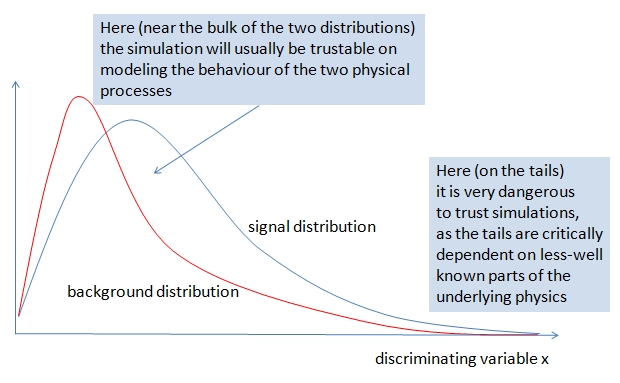
While when studying a single kinematical distribution it is easy to understand when one may rely on the simulation and when one should instead be careful, when one considers a multi-dimensional space of 30 variables things get murkier. The inputs to these Monte Carlo simulations are not only our theoretical knowledge of the physical processes producing the various particle reactions, but just as well a lot of modeling -of parton distribution functions that decide how large a fraction of the protons' momenta is carried by the partons that give rise to the actual subnuclear process; of the fragmentation of final state quarks and gluons into jets of stable particles; of the interactions that take place as those stable particles hit our detectors.
You clearly see that we have a problem. How can we be sure that we are perfectly simulating all corners of phase space of a 30-dimensional space ? We cannot. What we can do is to carefully work out estimates of the systematic uncertainty that our modeling brings in. The final "background estimate" of a tight multivariate selection is thus plagued not just by the statistical uncertainty, but by that systematical error. Now, it is very hard to estimate correctly a systematic uncertainty even when we discuss a single one-dimensional distribution; imagine how hard it becomes when we deal with 30 dimensions all together, and a complex algorithm we have no intuition about, which freely picks around this space the regions where more signal should be hiding.
Because of the problem with estimating the systematic uncertainty of a complicated selection, experimentalists usually try to not push the selection too far. More stringent, more optimized selections may suffer from larger systematical uncertainties because the stricter those selections are the larger is the uncertainty on the accuracy of the simulations in the narrow regions of phase space that gets selected as signal-rich. Because of that, there is a compromise to strike.
The compromise is usually the one of selecting variables one is relatively more confident that the simulation describe well, and to avoid pushing too far the investigation in the multi-dimensional space. You therefore understand that experimental physicists, while quite interested in understanding what are the software algorithms that produce the best discriminating power on specific problems, will not automatically let those algorithms run at their optimized points, but will rather interact with the software and restrict a bit its freedom to use too many variables or select too narrow regions of phase space.
Knowing the above, you understand why as an experimental physicist I do not feel disowned of my legitimate expertise as a data analyst - I may not always pick the most powerful classification method, but the reason is usually that one has to consider everything together when optimizing for a search - not just the statistical significance after the selection, but the systematic uncertainties that the method carries with itself.





Comments