You’ve heard that space is curved – that’s gravity. You’ve also been told that you cannot really understand curved space. Sure, you can come to know curvy mathematics by studying general relativity or differential geometry, but you cannot grasp curved space in your bones…for the obvious reason that, in our everyday human-level world, space is flat, and so we have a brain for thinking flat.

Or, at least, that’s what they say.

But there is at least one variety of curvy mathematics that your brain comprehends so completely that you don’t even know you know it. It concerns your visual field, and your innate understanding of the directions from you to all the objects in your environment.

In thinking about your visual field, it is best to imagine a sphere around your head, recording the directions to all objects in one’s environment. Call it the “projection sphere,” since it records in which directions objects project light toward us.

So, if you are standing in front of a row of six vertical poles, then they will project onto your sphere as shown below. In this figure, one imagines that you, the observer, are at the center of the sphere, looking in the direction of the cross.



Consider now the way these poles project…

First, notice that each pole appears straight in your visual field. They are not straight in the figure above, but remember that the observer in the figure is at the center of the sphere looking out. Each pole is straight on this projection sphere -- and thus in your visual field -- because each is what is called a “great circle,” extending in this case from the bottom to the top of the sphere like lines of longitude.

Second, observe that the poles are parallel to one another at the equator.

Yet, despite being straight lines that are parallel to one another, they intersect! Namely, the lines intersect at the top and bottom of the sphere.

Can this really be?

It can really be, and it is possible because of the non-Euclidean nature of the geometry of the visual field.   The geometry that is appropriate for the visual field is the surface of a projection sphere, and the surface of a sphere is not flat / Euclidean, but, well, spherical.

There are three main kinds of geometry for space: elliptical (including spherical), Euclidean (or flat), and hyperbolic.  How does one tell them apart? One way is to simply measure the sum of the angles in a square drawn in that space.

In Euclidean geometry, the sum of the angles in a square is 360 degrees. But for elliptical geometry the sum adds up to more than 360 degrees. In hyperbolic geometries, on the other hand, the sum comes to less than 360 degrees.  Back to the visual field, then, let’s “draw” a square on it and sum up its angles.



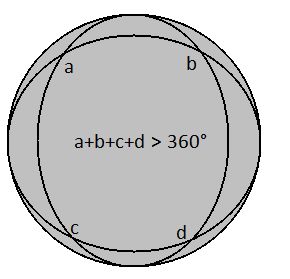
The figure above shows a square in your visual field. Why does it count as a square? Because (i) it has four sides, (ii) each side is a straight line (being part of a great circle), (iii) the lines are the same length, and (iv) the four angles are the same.

Although it is a square, notice that each of its angles is larger than 90 degrees, and thus the square has a sum of angles greater than 360 degrees.  The visual field is therefore elliptical, and spherical in particular.

One does not need to examine figures like those above to grasp this. If you are inside a rectangular room at this moment, look up at the ceiling. The ceiling projects toward you as a four-sided figure. Namely, you perceive its four edges to project as straight lines. Now, ask yourself what each of its projected angles is. Each of its angles projects toward you at greater than 90 degrees (a corner would only project as exactly 90 degrees if you stood directly under it).

Thus, you are perceiving a figure with four straight sides, and where the sum of the angles is greater than 360 degrees.

Your visual field conforms to an elliptical geometry!

(The perception I am referring to is your perception of the projection, not your perception of the objective properties. That is, you will also perceive the ceiling to objectively, or distally, be a rectangle, each angle having 90 degrees. Your perception of the objective properties of the ceiling is Euclidean.)

It is often said that non-Euclidean geometry, the kind needed to understand general relativity, is beyond our everyday experience, since we think of the world in a Euclidean manner. While we may think in a Euclidean manner for our perception of the objective lines and angles, our perception of projective properties -- i.e., the directions from us to the world around us -- is manifestly non-Euclidean, namely spherical.

We do have tremendous experience with non-Euclidean geometry, it is just that we have not consciously noticed it. But once one consciously notices it, it is possible to pay more attention to it, and one then sees examples of non-Euclidean geometry at every glance.

~~~

This piece was adapted from my book, The Brain from 25000 Feet (Kluwer). Mark Changizi is Professor of Human Cognition at 2AI, and the author of The Vision Revolution (Benbella Books) and the upcoming book Harnessed: How Language and Music Mimicked Nature and Transformed Ape to Man (Benbella Books).