For hundreds of years, mathematicians even as great as Leonhard Euler(1) have tried to make sense of partition numbers, the basis for adding and counting.  Progress has been made but there has never been a full theory to explain partitions.   Answers have always led to more questions.

Basically, partitions are not considered by some to be part of number theory at all but to keep it simple for now, in number theory, a partition of a positive integer (n) is a way of writing n as a sum of positive integers.    

Here is an example from the Classic Encyclopedia:

To form the partitions of 6 we take first 6; secondly, 5 prefixed to each of the partitions of 1 (that is, 51); thirdly, 4 prefixed to each of the partitions of 2 (that is, 42, 411); fourthly, 3 prefixed to each of the partitions of 3 (that is, 321, 3111); fifthly, 2 prefixed, not to each of the partitions of 4, but only to those partitions which begin with a number not exceeding 2 (that is, 222, 2211, 21111); and lastly, 1 prefixed to all the partitions of 5 which begin with a number not exceeding 1 (that is, 11111 I); and so in other cases.

Mathematicians love to count and counting the number of ways that a number can be partitioned has fascinated them since Euler made a dramatic breakthrough in understanding the partition function by writing down the generating series for it.


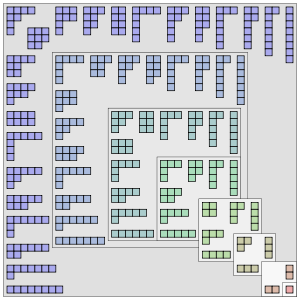
Ferrers diagrams showing the partitions of positive integers 1 through 8. They are so arranged that images under the reflection about the main diagonal of the square are conjugate partitions.  Credit: Wikipedia

Want to try it yourself without the pen and paper?  Wolfram Alpha has a web version.

Emory mathematician Ken Ono says he will unveil new theories that answer the famous questions about partition numbers and prove that partition numbers behave like fractals, which you may know as those gimmicky random things so popular in the 1990s. They say they have unlocked the divisibility properties of partitions, and developed a mathematical theory for "seeing" their infinitely repeating superstructure - and that they have devised the first finite formula to calculate the partitions of any number. 

"Our work brings completely new ideas to the problems," says Ono, who will explain the findings in a public lecture at 8 p.m. Friday on the Emory campus. "We prove that partition numbers are 'fractal' for every prime. These numbers, in a way we make precise, are self-similar in a shocking way. Our 'zooming' procedure resolves several open conjectures, and it will change how mathematicians study partitions."

"Ken Ono has achieved absolutely breathtaking breakthroughs in the theory of partitions," says George Andrews, professor at Pennsylvania State University and president of the American Mathematical Society. "He proved divisibility properties of the basic partition function that are astounding. He went on to provide a superstructure that no one anticipated just a few years ago. He is a phenomenon."

The work was funded by the American Institute of Mathematics (AIM) and the National Science Foundation. Last year, AIM assembled experts on partitions, including Ono, to attack some of the remaining big questions in the field. Ono, who is a chaired professor at both Emory and the University of Wisconsin at Madison, led a team consisting of Jan Bruinier, from the Technical University of Darmstadt in Germany; Amanda Folsom, from Yale; and Zach Kent, a post-doctoral fellow at Emory.

NOTE:

(1) Euler gets mentioned a lot around here but he was not a one-dimensional math guy.  He could repeat Virgil's Aeneid from memory and even tell people the first and last line of any page in the edition which he used.