"In 1934, L.E.Kinsler at the California Institute of technology was studying the Zeeman effect as a means for evaluating the charge-to-mass ratio of the electron, e/m. The deduction of e/m from the measured wavelength differences involves, in addition to a high-precision measurement of the magnetic field, a knowledge of the way in which the individual electron spins and orbital angular momenta are coupled. However, there are certain quantities or combinations of quantities that are independent of the nature of the coupling. 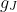One such combination is provided for by a relation called the g-sum rule, which states that the sum of the values of for all the states with a given value of J formed from a given combination of single-electron states is independent of the coupling. Kinsler undertook to test this rule, using two states in neon that involved five electrons in 2p states and one in a 3s state.[...]
Kinsler's measurements gave , .
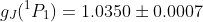
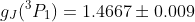
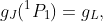
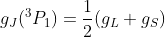
The discrepancies from the values are substantial but are presumably to be ascribed to the imperfectness of the L-S description. The g-sum rule is another matter: .
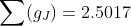
Kinsler simply added the errors on the individual values and quoted a resultant error of 0.0016, so that the discrepancy was regarded as insignificant. [...] If the individual errors were independent, a better overall uncertainty would have been the square root of the sum of the squares, or 0.0011, making the discrepancy large enough to be taken seriously. [...]
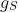
Even if Kinsler had believed his result, however, the tone of his paper suggests that he would have ascribed it to the failure of the g-sum rule rather than to an anomalous value of . On such minor things does the course of events depend!"

George L. Trigg, Landmark Experiments in Twentieth Century Physics, Crane (NY) 1975.