When heavy nuclei collide at very high energy, they are thought to create, for a very short time, a hot plasma of hadronic matter which is unlike anything else in the Universe today. Proton-proton collisions do not do that, because there are too few energetic partons around to create a significant "blob". The comparison between what we observe in heavy ion collisions and proton-proton collisions taken at the same equivalent energy allows us to draw some interesting conclusions on the behaviour of this plasma.
In a hot plasma of quarks and gluons, it should be harder for stable hadrons to retain their binding. So one specific signature of the creation of this extreme condition of matter is the fact thaw we should detect a reduced yield of heavy mesons -bound states of heavy quark-antiquark pairs which are not the typical product of normal parton fragmentation processes, but which are indeed produced by the hard collision. Ok, but what kind of mesons should we go after ?
Of course, we need to focus on mesons whose creation occurs at the instant of the hard collision, and whose presence we detect with great precision: ones which are unmistakable even in the horrendous mess created by a collision of hundreds of nuclei in simultaneity. This makes the Upsilon meson, a bound state of a bottom-antibottom quark pair, an ideal testing ground: the Upsilon and its excitations (labeled by their angular momentum: 1S, 2S, 3S... in ancient spectroscopic notation) decay to muon pairs, which escape unharmed the hot soup, and get detected with precision in the outer detecting elements of CMS.
Where Have All The Upsilons Gone ?
Have a look at how we see Upsilon particles below: the three resonances 1S, 2S, and 3S stand out of backgrounds very cleanly in proton-proton collision data. Their mass is reconstructed easily from the measured momentum of the escaping muons.
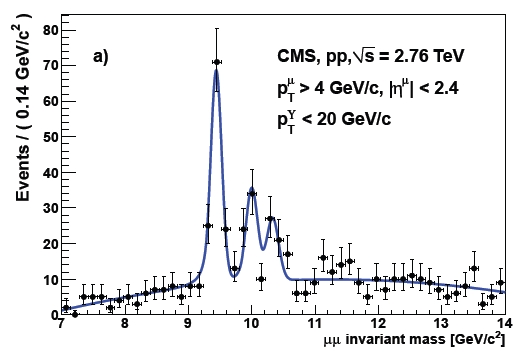
And now look at the same graph obtained from the lead-lead collisions. Is there something strange going on here ? Indeed the 2S and 3S states appear to have vanished -or at least to be strongly reduced from the yield they showed in proton-proton data. The ratio between production of 1S and (2S plus 3S) states should be the same in the two datasets, because the production of these hadrons is governed by the same mechanisms: a nucleon is a nucleon is a nucleon for the strong force... But it apparently isn't!
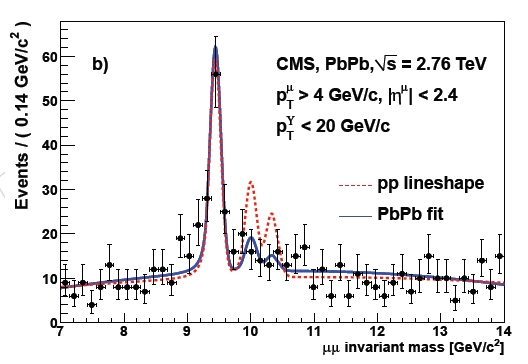
(Two words of explanation of the graphs: the black dots with error bars show the dimuon invariant mass in the data -respectively proton-proton collisions in the top figure and lead-lead collisions in the bottom figure; the blue curves show the result of unbinned likelihood fits to the mass spectra, using some fixed parameters to aid the fit, such as the mass difference of the three states fixed to world average value. The red hatched curve in the bottom figure reports the expected yield of signal in lead-lead collision data from the yield observed in proton-proton collisions. The background is allowed to vary shape parameters in each fit).
The suppression of the excitated Y states is predicted by the "melting" of these bound states in the quark-gluon plasma. Since the 2S and 3S resonances are less tightly bound than the 1S, they melt more readily in the high-temperature environment, and we see fewer of them. This, at least, is the suggestion of the analysis, which finds a 2.4-sigma deficit of 2S and 3S candidates with respect to 1S candidates in lead-lead collisions, taking the relative yield in proton-proton collisions as a reference.
2.4 standard deviations from a unit ratio is not a huge effect, and the possibility that we are just hyping a statistical fluctuation does exist. However, I tend to believe that this signal is genuine. Time will tell, of course, when more heavy ion collisions will be recorded by the LHC experiments. Also, ATLAS and ALICE will also produce results on this effect, I am sure.
An interesting note - for experts only
Now, for experts I would like to add something at the bottom of this post. What experiments claim in observations of this kind is a "suppression of particle production". They mean that the bottom-antibottom resonances are not forming in the hot gluon plasma, because of the dense environment and its complicated dynamics. I question the validity of this assertion, both from a theoretical and from an experimental point of view.
Theoretically, what we might envision is that the bottom-antibottom pair gets created and does bind; the resonance then has a relatively long lifetime because quantum chromodynamics can only disintegrate it by letting the pair emit no less than three gluons (the Okubo-Zweig rule). In short, one gluon cannot mediate the disintegration because the Y is colourless; two gluons have the wrong C-parity, which is a conserved quantity in strong interactions; so three gluons are the minimum. The simultaneous emission of three gluons is thus an alpha_s^3 effect, and is thus suppressed enough that the competing decay to dimuon pairs through an electroweak annihilation diagram emerges a significant fraction of the time (a few percent). Thanks to all this, we do detect the Y decay!
Now, the point. In a hot gluon plasma, the resonance can exchange degrees of freedom more readily, and the conservation of colour or C-conjugation quantum numbers may be taken care of by the plasma itself. If the strong decay then proceeds more readily, the electroweak process is suppressed.
Experimentally, we count only dimuon decays -we do not have any access to measuring the hadronic branching fraction!-, so we observe a deficit. That deficit is the result of the suppression of "production cross section times branching fraction into dimuon pairs", and not just suppression of the production!
I think this is a subtle point which I have however never heard disproven in a conclusive way. I would be very, very happy if some of you knowledgeable readers could shed some light for me into the (hot) matter. Thanks!
Further reading: see here.





Comments