The Tevatron collider has been shut down for almost half a year now, but the CDF experiment is still busy producing world-class measurements of fundamental Standard Model parameters.

Actually, the above is not quite correct: CDF is re-defining "world class" in some cases. The measurement I am going to describe, which has just been made public (if you are quick you can follow live the seminar presented by Prof. Ashutosh Kotwal at Fermilab here), totally outperforms all previous determinations of a crucial ingredient of the Standard Model: the W boson mass.

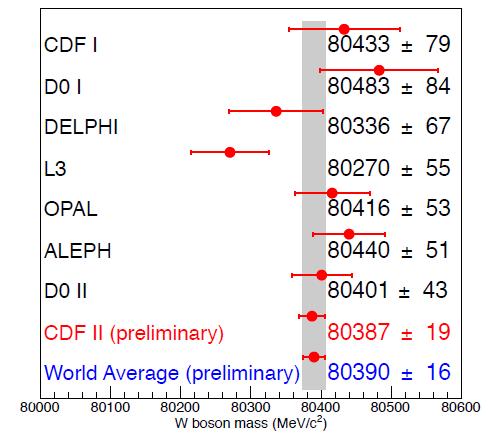
Before the new CDF result, we knew the value of the W boson mass with a 23 MeV uncertainty by averaging several precise determinations, including those produced by the LEP II experiments (a true "W factory": there, the four experiments obtained the W mass with uncertainties varying from 51 to 67 MeV) and by the DZERO collaboration (43 MeV uncertainty). Now the total error of the world average has shrunk to 16 MeV, thanks to the CDF result, which alone has a 20% better precision than the world average of seven other measurements together. In other words, the 19 MeV uncertainty of the CDF determination puts it in another category with respect to the past results.

A detailed description of the measurement would be impossible for this blog. I only wish to explain the general ideas and the difficulties of the analysis. First of all, CDF uses two different decay modes of the W bosons produced in the 2-TeV proton-antiproton collisions: decays to electron-neutrino pairs, and decays to muon-neutrino pairs.

Electrons and muons provide a quite distinct signature in the CDF detector: the former yield a stiff track in the inner tracking chamber, coupled with a localized energy deposition in the first layers of the calorimeter, due to the electromagnetic shower that the electron creates upon "braking" in the strong electromagnetic field of high-atomic-number material. Muons, on the other hand, produce a similar track in the inner tracker, but only deposit some 2-3 GeV of energy in the calorimeter, punching through it and leaving additional hits in special "muon detectors" located outside of the calorimeters.

The identification and measurement of electrons and muons are by themselves already sufficient to prove the presence of a large sample of W boson decays in CDF data; but the additional signature of energetic neutrinos makes the W signal unmistakable and very clean. Neutrinos are unseen in the detector, but the momentum they carry away leaves a very clear footprint, in the form of a unbalancing of the total momentum observed to flow transversely from the beam direction. We observe a "missing transverse energy" which measures the transverse component of the neutrino momentum.

Once the data is properly selected, the signal to noise ratio is several tens to one, which makes these samples a rare treasure for a HEP analysis: despite the intrinsic quantum indetermination of subatomic processes, we can bet to very high odds that each one of those events is a real W decay.

The measurement of the W boson mass is performed by a combined fit to three kinematic quantities for each of the two datasets (electron-neutrino pairs, and muon-neutrino pairs): the transverse momentum or energy of the charged lepton, the missing transverse energy, and the transverse mass of the two-body system. The transverse mass is the mass reconstructed by using only the transverse components of the leptons momenta: the longitudinal component of the neutrino momentum is in fact unknown, since in proton-antiproton collisions the center-of-mass of the collision does not coincide with the laboratory system, and moves along the beam with unknown energy, non measurable.

Because of the missing longitudinal information, the "transverse mass" has a shape different from that of a resonance: it is not a Breit-Wigner, but rather a "Jacobian peak", sharp on the right edge, and more blunt on the other. The requirement of 30 GeV of transverse energy to the two decay products however makes the shape more symmetrical than it would be otherwise.

Below you can see the transverse mass reconstructed in the electron-neutrino final state,



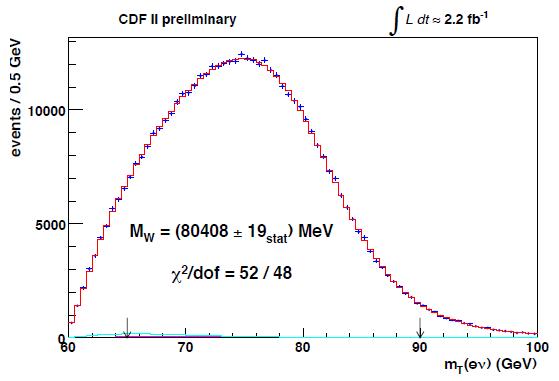
and the one from the muon-neutrino final state.



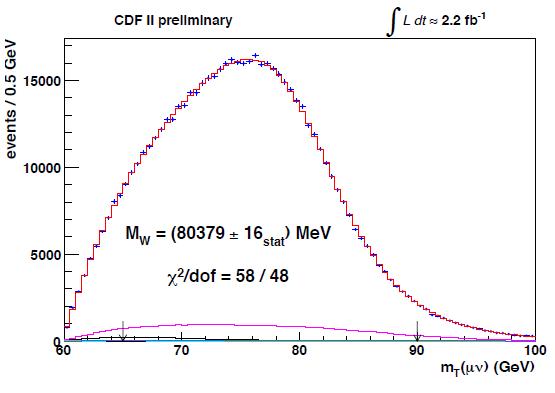
The red curves show the fit to the data points, which have tiny error bars, due to the very large data samples employed in the analysis (ones corresponding to a total integrated luminosity of 2.2 inverse femtobarns, corresponding to 200 trillion collisions).

The difficulty of the measurement does not lay in the precision fit to the kinematical distributions. Rather, the challenge is to calibrate the measurement of the observed quantities, and reduce the related systematics as much as possible.

For example, we need to know with extreme accuracy the exact value of the magnetic field that the charged particles traverse, as a function of the position in the tracker. This is needed in order to derive from the track curvatures a precise estimate of their momenta. The calibration is performed by studying large samples of two-body decays to muon pairs: J/psi mesons, Upsilon mesons, Z bosons. These particles have been measured very precisely in the past, so a comparison of the reconstructed mass of the CDF signals allows to calibrate the track momentum measurement.

A unrelated systematic uncertainty which is very tough to reduce is the one coming from the knowledge of parton distribution functions in the proton. It comes into play because the shape of the kinematical distirbutions from W decay are affected by the energy of the initial state partons that give rise to the W production process. If there are more partons at low energy than there are at high energy, then the observed W mass, which is normally a Breit-Wigner distribution deformed only by final state radiation effects (energy lost to photon radiation) gets "skewed" toward smaller mass values, simply because more of them are produced at a mass slightly lower than the center of the Breit-Wigner than are produced at a higher mass.

Another difficult effect comes from the modeling of the QCD radiation off the partons that produce the W. The amount of transverse "boost" of the W boson, received from the recoil off a energetic gluon or quark, modifies the shape of the transverse momentum distribution of the decay leptons. A precise model of the effect is required in order to correctly fit for the W mass from the lepton transverse momenta. The QCD radiation recoil model is studied in Z decays, since Z boson decays undergo the same effect. A comparison of models of Z transverse momentum with the real data distributions allow to constrain the effect and tune the simulation from which the shapes of the kinematical variables are deduced.



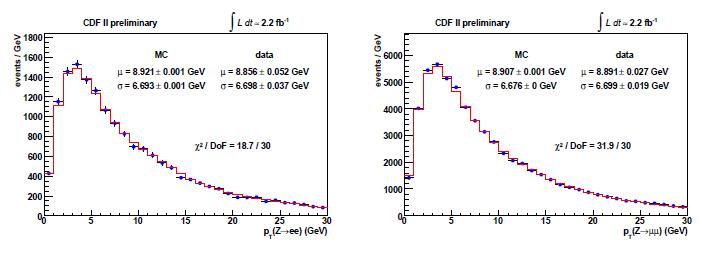
Above you can see how the CDF data for the transverse momentum of lepton pairs from Z boson decays (left: electron-positron pairs; right: muon pairs) compare to the simulation: the possible small mismatches have an impact in the final determination of the W mass.

After all the tiny effects that can compromise the precision of the main measurement are painstakingly investigated and sized up, CDF can fit the six distributions together. The statistical uncertainty which results from the combined fit is very small, which explains why the measurement is produced with "only" 2.2 inverse femtobarns of data: using the full 10/fb dataset of Run II collisions collected by CDF in the last 10 years would only cause a large overburden to try and understand to a high level of detail the larger systematics brought in by varying data taking conditions and other calibration issues.

The final result is


which has a relative precision of one part in 4231, i.e. a 0.0236% error. By combining this with previous determinations the new world average for the W boson mass is of


The result is compared to previous determinations in the figure below.



It is interesting to know that global fits to electroweak observables using this new information now indicate for the Higgs boson mass a value in the range 67-119 GeV. The 124-126 GeV signal of the CMS and ATLAS collaborations is after all not in disagreement with this fit, being just a tad over one-sigma away from the indirect information best value (90 GeV).

I think the present W mass measurement is the best final gift that the experiment could give to all of us, after 28 years of illustrious career. The LHC experiments will have a very hard time improving the precision of the W mass further. But of course, many other measurements are still being produced by CDF and DZERO, and this will continue for at least one more year...