You of course do not need to be reminded that Supersymmetry is not a theory but a framework, within which a host of possible manifestations of subnuclear physics are configurable based on the value of 120-or-so free parameters. Because of that, if one wants to discuss in detail what are the most likely versions of SUSY left on the table, and what is the value of the most representative and critical theory parameters, one needs more than paper and pencil.
A 30-page article is a better shot if one wants to give the flavour of how the recent experimental constraints combine with earlier data to provide best-fit values for tan(beta), M_A, M_0 and M_1/2, etcetera; and a constantly updated web page is still better. So let us see what Sven's group has produced for us. Okay, okay - I will try not to be lazy and give recognition straight off: the authors of the study I am discussing are O. Buchmueller, R. Cavanaugh, D. Colling, A. De Roeck, M.J. Dolan, J.R. Ellis, H. Flacher, S. Heinemeyer, G. Isidori, D. Martınez Santos, K.A. Olive, S. Rogerson, F.J. Ronga, and G. Weiglein.
The paper is titled "Supersymmetry and Dark Matter in Light of LHC 2010 and XENON 100 Data". Yes, I know. 2010. But keep reading and you'll be rewarded.
The analysis focuses on minimal-minimal versions of the MSSM, to facilitate the discussion. And the MSSM is of course the minimal supersymmetric extension of the Standard Model, i.e. the one which introduces the smallest amount of extra parameters possible (about 100). Of course: when you have such a beast to deal with, you are forced to simplify matters a bit. The paper considers four specific versions of the MSSM: a constrained version, CMSSM, where the soft SUSY-breaking mass parameters are assumed to be universal at a very high energy scale where theories unify; the NUHM1, which relaxes the previous constraint to allow freedom in the Higgs boson masses; a variation of the former called VCMSSM (I know, we're running out of alphabetical signs with these theories!), and the good-old mSUGRA model. Details in the paper.
For each considered model, the group analyzed the effect of the new LHC measurements based on the 2010 data sample, as well as a few additional results obtained with 2011 data, and they included in the analysis the results obtained by the XENON 100 collaboration, which is looking for a direct signal of dark matter particles and produced constraints in the spin-independent cross section of these particles in nuclei.
The method of investigation chosen is a frequentist analysis, whereby the data are included in a likelihood function which is then sampled in the interesting subspaces of the parameter space, obtaining nice coloured bidimensional figures which describe where is the bulk of the probability. This is performed with a tool called "MasterCode", which employs the Markov Chain Monte Carlo to sample million of space points. MasterCode allows to incorporate new constraints in older samplings by evaluating their impact on the likelihood, sizably simplifying the work.
The paper is quite extensive and describes each input in detail, examining what impact the new measurements have on the relative probability of different points in the parameter space. I have no chance to provide an exhaustive summary, so let me peek at the results for the mass of the gluino in the four considered theories. A picture is shown below.
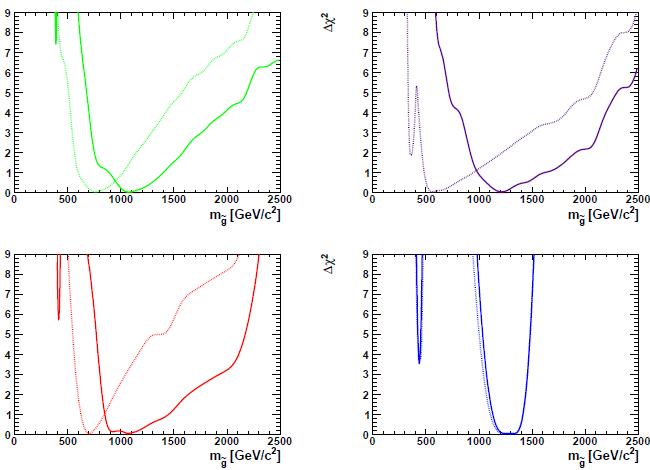
From left to right and from top to bottom, the four theories considered in the graphs are the CMSSM, the NUHM1, the VCMSSM, and mSUGRA. The hashed lines are previous best-fit values, the full lines include the new LHC results. Bear in mind that what is plotted is always the delta-chisquare from the minimum (eg. the maximum likelihood value): of course, the "likelihood" that these parameter values describe the reality of Nature has decreased given the null search results. And as expected, the preferred mass value of the gluino generally moves up as new LHC results are included in the fit. All theories considered are now pointing at gluinos with masses exceeding one TeV.
Despite the above moving up of gluino masses, the best fit points overall do not move dramatically after the inclusion of the new inputs. As the authors comment in their summary,
The negative results of the searches to date are not in serious tension with the ranges of parameter spaces favoured pre- LHC in the models we have studied. The favoured regions yet to be explored offer good prospects for the SUSY searches during the LHC run in 2011/12. However, it is worthwhile to consider whether the exclusion by the LHC of very light squark and gluino masses may already have messages for future experimental studies of supersymmetry (if it exists).
Wow. Die-hard SUSY aficionados such as my friends Sven and Albert are now adding disclaimer brackets to their summaries! I am impressed. Recently I commented that the failed 2010 searches for SUSY at the LHC was already starting to worry theorists. Now I receive positive confirmation in print. Indeed, the authors continue their summary by examining the impact of these results on the possible design of a next linear collider. I prefer to keep myself on the ground and claim that if the LHC sees nothing, I doubt we will be discussing whether 500+500 GeV are enough or 600+600 would be better, and similar angel's sex issues. But I congratulate with the authors of the study for a very extensive survey.
Of course, those of you who frowned when I first mentioned 2010 data are now wondering what are they still doing here. That's right: you should visit the MasterCode web site, where updated results are shown and compared to the latest 2011 limits! I decided to discuss the paper here, but maybe there's space for one more figure:
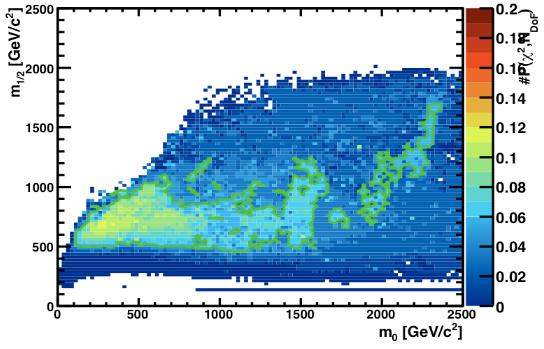
This is the M_0 - M_1/2 parameter space of the CMSSM after the inclusion of 2011 results shown at EPS! The colours provide the fit probability, and the green line encompasses areas with a fit probability better than 5%. The best-fit probability is 11%!! Does this mean that the CMSSM is practically excluded at 90% CL over all the parameter space ? I turn this question to Sven.





Comments