Introduction

It is a mathematical fact that both the real numbers and the rational numbers contain an infinite amount of elements. It is possible to devise a procedure that assigns a label containing a different natural number to every rational number. This is not possible for the real numbers. Technically this means that the set of real numbers has a higher cardinality than the set of rational numbers. In simple words it means that there are far more real numbers than there are rational numbers. Still both sets can densely cover a selected continuum, such as a line. However, the rational numbers leave open places,because infinite many real numbers fit between each pair of rational numbers.

Complex numbers and quaternions have the same cardinality as the real numbers. They all form a continuum. Rational numbers have the same cardinality as the integers and the natural numbers. They all form (infinite) countable sets.

Now take the fact that the set of observations covers a continuum and presume that the observed objects form a countable set. This poses a problem when the proper observation must be attached to a selected observed object. The problem is over-determined and in general it is inconsistent. The problem can only be solved when a little inaccuracy is allowed in the value of the observations.

In quantum physics this inaccuracy is represented by the wave function, which is a probability amplitude distribution. It renders the inaccuracy stochastic.

Quantum physics uses separable Hilbert spaces as the realm in which it does its mathematics. A separable Hilbert space has only a countable set of dimensions. So, a location-operator can only have a countable set of eigenvectors. Each eigenvector represents a location. As a consequence, only a countable set of relevant locations exists. That is why wave functions must solve the problems that are posed by the availability of a too large variety of observations.

In the Hilbert Book Model this argument is used in order to explain why physics contains fields, thus it has far reaching consequences. One could apply non-separable Hilbert spaces, such as a rigged Hilbert space, but that takes the argument away why physics must contain fields.

Probability amplitude distributions

The wave function of physical particles is a typical example of a probability amplitude distribution. Most physicists use a complex probability amplitude distribution (CPAD) for that purpose. The squared modulus of a CPAD can be interpreted as the distribution of the probability density of the presence of the carrier of the properties of the particle. However, it is equally well possible to use a quaternionic probability amplitude distribution (QPAD) instead of a CPAD. This option has several advantages. A QPAD can be considered as the combination of a real charge density distribution and an imaginary current density distribution. What these charges and currents are, can be left to later investigation. It is appropriate to interpret the charge as the ensemble of the properties of the carrier of the charge. As with the CPAD, the squared modulus of a QPAD can still be interpreted as the distribution of the probability density of the presence of the carrier of the properties of the particle. The main difference is that with QPAD’s fundamental physics can be interpreted as a streaming problem.

This can be taken one step further. This occurs by deliberating about the carriers. What can they be? A daring and at the same time promising choice would be that they are tiny patches of the parameter space of the QPAD. The parameter space can be seen as the imaginary part of a quaternionic distribution. By transporting tiny patches out of that space to another location the space can be locally compressed and may extend at other locations. In this way a kind of space-atmosphere is created.

This daring interpretation immediately gives an explanation for the existence of space curvature in the neighborhood of particles.

Sign flavors

QPAD’s have still another advantage above CPAD’s. Quaternions have two independent sign selections, where complex numbers have only one. One of the sign selections works isotropic. It is called conjugation and switches the sign of all three imaginary base vectors. The other is a reflection and exists in three independent directions. As a consequence eight different sign selections exist. This fact is hardly known.

Quaternionic distributions keep the same sign selection through all of their values. Thus quaternionic distributions exist in eight different sign flavors. Usually their parameter is a quaternion or the imaginary part of it. Thus the parameter space is itself a quaternionic distribution. This opens the possibility to use the parameter space as the reference for the characterization of the sign flavor of the quaternionic distribution.

QPAD’s are just special kinds of quaternionic distributions.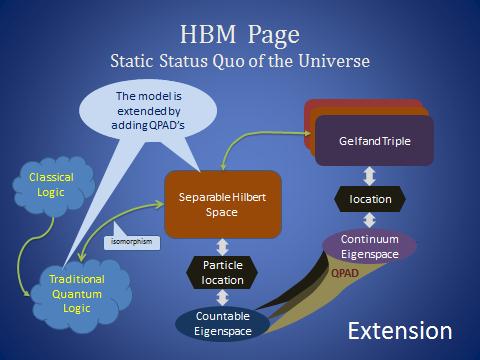

The Hilbert Book Model

The Hilbert Book Model (HBM) is a simple Higgsless and self-consistent model of fundamental physics that is strictly based on the axioms of traditional quantum logic. It uses a sequenceof instances of an extension of a quaternionic separable Hilbert space that each represents a static status quo of the whole universe. It widely uses the opportunities that are offered by QPAD’s. The HBM uses the sign flavors of coupled QPAD's in order to construct all known elementary particles that occur in the standard model.

Due to its reliance on QPAD’s rather than on CPAD’s its methodology is unconventional and rather controversial. Methods that work in QDE and QCD cannot all be applied in the HBM. However, the HBM offers circumventions for this dilemma. It treats linear equations of motion such as the Dirac equation as balance equations. It treats fundamental physics as a space streaming problem.

See: http://vixra.org/abs/1112.0084 and http://vixra.org/abs/1202.0033