Hello!
I join the revolution, with a contribution. :)
-----------------------------------------------------------------------------------------------------------------------------------------------
The year 1900.
1) Planck made the crucial discovery:
(
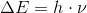
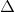means that this energy is the elementary energy which is finite)2) In the same year, Henry Poincare wrote and published the paper
http://fr.wikisource.org/wiki/La_th%C3%A9orie_de_Lorentz_et_le_principe_...
where he derived the equation for mass-energy relation
arxiv.org/ftp/physics/papers/0608/0608289.pdf (page 2)
http://en.wikipedia.org/wiki/Henri_Poincar%C3%A9#Mass.E2.80.93energy_rel...
“Poincaré concluded that the electromagnetic field energy of an electromagnetic wave behaves like a fictitious fluid ("fluide fictif") with a mass density of E/c2.”
http://en.wikipedia.org/wiki/Henri_Poincar%C3%A9#Poincar.C3.A9_and_Einstein
“A few years before his death, Einstein commented on Poincaré as being one of the pioneers of relativity, saying "Lorentz had already recognised that the transformation named after him is essential for the analysis of Maxwell's equations, and Poincaré deepened this insight still further ...." [35] ”
3) Newton’s law of gravitation was known for a long time already.
(According to GR, the Newton’s law of gravitation is just an approximation. But, during the course of these posts, it will become completely clear that the situation is exactly opposite, namely, that the GR equations are approximations of reality, which are good in the area which is far away from the Schwarzschild radius
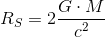
and become more and more wrong as we approach the Schwarzschild radius, and, finally, become totally wrong at the Schwarzschild radius.)
So, if I were Poincare, or somebody else who lived then, I would have tried the following theoretical investigation/derivation about how would an EM quantum energy (which, a few years later, will be named as “a photon”) behave in the gravitational field.
The intensity of the gravitational force is
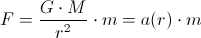
where
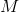is, for example, the Earth’s mass, and 
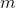is the mass of an entity within the Earth’s gravitational field.The amount of work which has to be done in order to move the mass
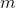infinitesimally radially away from Earth, 
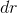, is
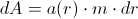
In the case of a photon which moves radially away from Earth, and according to the energy conservation principle, and according to the equation which Poincare had derived, we would have
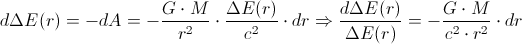
from which we easily obtain the Pound-Rebka experiment result:
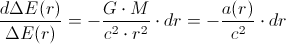
The height of the Pound-Rebka measurement platform was 22.5m.
That is much, much less than the Earth's radius, so we can use the approximations
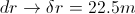
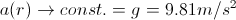
and we get that the ratio of the photon's energy change and the photon's energy is
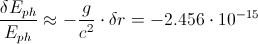
We could also obtain the exact equation for calculation of the red-shift.
From the equation
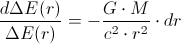
we first derive the equation which describes the behavior of photon's energy in the gravitational field:
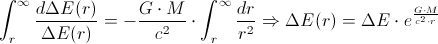
where
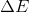is energy of the photon when it is infinitely away from the gravitation source (or, practically, when it so far that the gravitational influence is neglectable).And, the exact equation for red-shift calculation would be
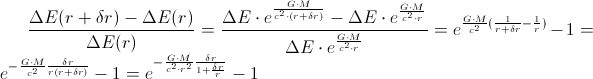
So, we can use this equation to calculate the exact red-shift, but the result will be practically the same as the result which we have already obtained, using the previous approximative calculation. Or, if we use the following approximation:
Since the exponent is very small, we have
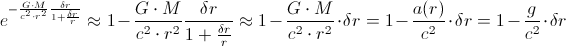
Hence, we get again
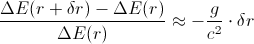
A photon is an elementary EM-oscillation which propagates linearly through the space.
An oscillation has the frequency. Frequency is the reciprocal value of the time period in which one full oscillation is performed.
So,
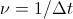
which means: the frequency of some oscillation is 1 full oscillation in the time period during which that oscillation completes.
Also, during the time period
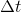, the photon travels the distance which is equal to its (wave)length.The least amount of energy for some given frequency is
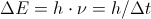
The least amount of energy means: the energy can be equal to or greater than that least amount, and the mathematical notion for that is
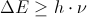
that is,
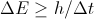
that is,
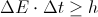
For a single photon we have
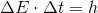
This equation universally defines/determinates the state of each and every photon:
- for some given energy, photon's EM-oscillation-period has to be such that the product of that energy and that time period is equal to h.
Or:
- for some given EM-oscillation-period, photon's energy has to be such that the product of that energy and that time period is equal to h.
Hence,
If the energy of a photon does change (i.e. as the photon moves away from the gravitational source), then the photon's EM-oscillation-period does change too, in the way that the product of their current values is equal to h:
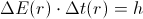
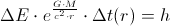
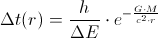
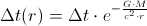
where
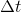is the oscillation-time-period of the photon when it is infinitely away from the gravitation source (or, practically, when it so far that the gravitational influence is neglectable).Through some fixed point which is infinitely far from the gravitation-source (or, practically, which so far that the gravitational influence is neglectable), the photon would pass in
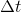time units.Through some fixed point which is in the vicinity of the gravitation source (i.e. Earth), that same photon would pass in
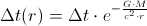time units.In that given, observed, fixed point, which our photon is passing through, an infinitesimal time-fraction of the photon's oscillation-period would be
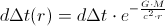
An infinitesimal time-fraction of the photon's oscillation-period is, generally, an infinitesimal time, so
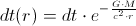
Knowing that the gravitational acceleration is
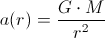,and that
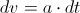,we will derive the velocity-equation of a photon which moves through the gravitational
field:
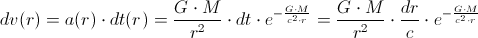
So,
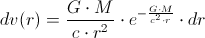
Or,
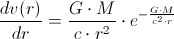
The differential of the
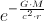is: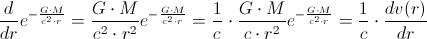
Hence,
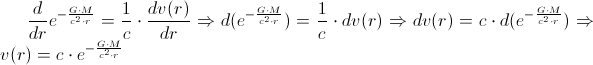
And, the length element of the photon’s path would be
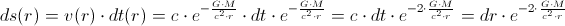
So, the single photon, that tiniest and most fundamental entity in universe, we have used as – so to say – the finest “litmus-paper” for discovering the space- and time- “flavors” of gravitational field:
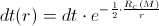
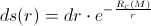
Here we’ve introduced
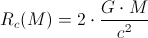
It has the dimension of length, and it depends on M. Since it is, so to say, the normalization factor for the radial coordinate r (or, for the radius r), we can call it “the characteristic radius of the body whose mass is M”. (That is how Planck, or Poincare would have probably named it, if they would had been those who did the previous derivations, in the year 1900.)
So, all this could had been derived in 1900 – from the existing knowledge at that time.
What we know now is that the Newton’s law of gravitation is very, very accurate:
http://physics.aps.org/story/v7/st8
http://arxiv.org/pdf/hep-ph/0405262.pdf
Hence, according to everything presented so far, the equations
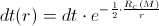
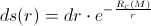
are logically, mathematically, and physically quite correct.
In the next post, we will use them to calculate the precession of planetary orbits, Shapiro time delay, gravitational deflection of light.
