Space seems like an empty box that lives
through time. This can already be classified as a “better model”, as you can
see in the table below. However, this tacitly held model makes people wonder:
If I toss a coin and find myself with the result being “tails”, where is the other me, the one who
found “heads”, the other possibility which physics can no longer ignore, and which
good philosophy has always known to be equivalent?
Has a universe popped up
next door to this one?
The question “Where are the other outcome worlds?” is similar to “Where are the other times, for example tomorrow, where is it?” The answers are thus similar.
Great philosophers like Kant and Wittgenstein knew half
of the answer implicitly; they understood the ‘apriority’ of space, time, and
causality. Modern physics clarifies it, making it palatable to the common intellectual.
We physicists provided first empirical data that were incompatible with naïve
models, but proof alone does not convince.
More importantly, we provide better visually
intuitive models, such as Minkowski’s space-time diagrams in case of Einstein’s
special relativity, and now the Einstein-Podolsky-Rosen Many-World model in
case of relativistic quantum theory.
So where is tomorrow, where are the
parallel worlds? They are not anywhere.
Or you could as well say that they are right here, because this is the place we
are talking about, namely you near that tossed coin, but at another time,
tomorrow, or being in a slightly different configuration, heads instead of
tails. “When” and “how”, not “where”! However,
we strongly desire to point to a place inside a space, a model, and we are not
satisfied until we can – I personally did not rest for many years until I
had a geometrical model of parallel worlds, all the time fully aware of the
fundamental silliness, perhaps impossibility of the endeavor.
Luckily, it
turned out to be possible.
This is what the common box, space-time, and many-world models are about. They allow our mind to consider the issue in familiar ways, namely those of a hunter-gatherer with a visual cortex so impressive that his nose has become obsolete. Humans ‘understand’ such issues if they can imagine a model with places and paths where they can point their fingers: “Here is the past, and there is the future, and that is a path of light from here to there, and now you see.” All of a sudden we have insight; the difficult has become trivial.
Quantum mechanics is very similar to relativity theory and even similar to the common box model already in this sense: The box includes all locations together, relativity theory is about including also different times properly, and quantum mechanics is about furthermore including all relevant possibilities, too – these connections are illustrated in the table below. Our intuition decreases with decreasing accessibility (top yellow row), so we have to work harder to grasp the model.
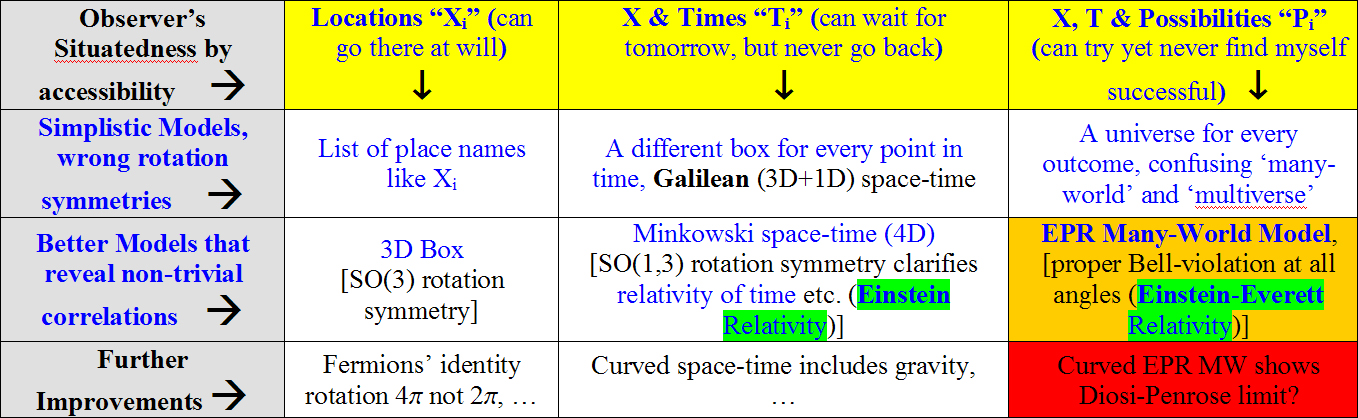
Overview of models: The blue text is understandable through this article. Orange background: This decade’s cutting edge, not yet known to mainstream. Red: Hypothetical, may be wrong! (Original work, please use, but please use with proper attribution)
If you want to model not only different places
in a three dimensional (3D) space but also different times, you need four
dimensional (4D) structures, which are listed in the third column in the table.
Space at a certain time is then a 3D “cut” through that 4D structure, a cross
section. This is *not* yet Einstein relativity
theory!
We are now inside the second row of the table; the better models
are in the row below. Einstein’s special relativity is: observers who move
relative to each other disagree on the orientation of the cut: If I move
relative to you, my 3D “box-right-now” has only a 2D slice in common with your
box-right-now; all my other parallel 2D slices are at different times
relative to you.
Note: this is not just about mere location and time labels. Measured lengths differ and twins can meet in the future having aged differently (the twin paradox).
Something very similar happens in quantum physics. Not only are different outcomes included (fourth column). That is true, but naïve many-world models that are confused with the concept of the multiverse (almost all science writers etc. confuse this - see here and here for the crucial difference!) do not have the correct symmetries. Again, the proper ‘Everett relativity’ becomes obvious in better models in the row below.
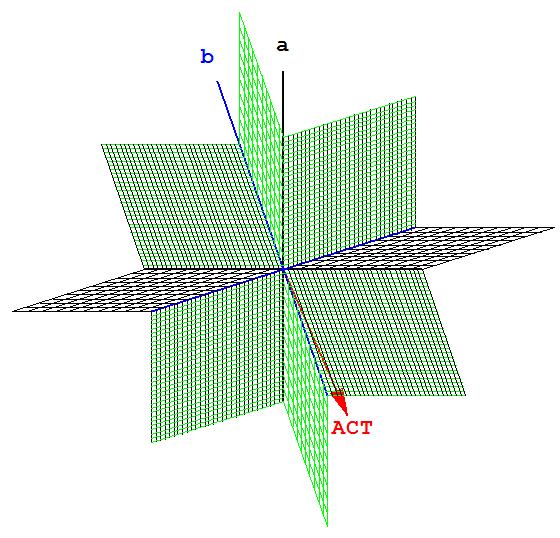
Locations, times, and now also outcomes depend on the observer’s situation. Again, this is not merely about different labels. At a certain angle in the EPR experiment, the Alice that observes 0 meets a Bob who got 1, while the Alice that got 1 finds a Bob that got 0.
Cross section of an EPR MW model with correct quantum probabilities (the classical-to-quantum transition model is simpler): Every small area is a parallel world of Carl as he observes the measurement results from Alice and Bob. Source: [1] and more explanation here.
Let us briefly review in order to reveal a problem: The 3D box is a useful model in everyday life and classical physics. In physics books, we see 2D pictures of the 3D model. If you want to understand time, the 3D box is a misleading model. You need 4D Minkowski space-time. Still, our pictures are mostly 2D. For understanding probability better, 4D space-time is insufficient. You need something that includes not just different times, but different possibilities. This is why there are now many-world models. So far so good, but the problem with them is: They have many more dimensions. 2D slices like the one above need a lot of explanation. Nevertheless, there are these comprehensible representations now and there is a touchable 3D model possible, too! Finally we have the satisfaction of understanding like a human must understand:
“Look, there is Alice finding tails and there is Bob finding heads.”
“But where are Alice and Bob both finding tails for example?”
“Right there at that angle.”
“Oh, yes, and I see right away that there are so few of those possibilities. Nice, but wait; do they find the quantum probabilities? Does the model violate the Bell inequality?”
“Well, go ahead and count, there and there ... , you can put your finger on them and count now. Then rotate the angle further and count again.”
“ … Oh, wow … but … the model is actually so simple … ”
A new version of the introduction to the EPR-MW model has just today been made available – it is yet more accessible to lay persons and has many simple drawings that slowly increase in complexity until the above 2D picture can be fully understood. Be one of the first people in the world who already understand this exciting model and its significance for science and philosophy; connect it with your creative work before everybody else catches up.
---------------------
Remark: Einstein-Everett relativity is almost unacceptable to our socially evolved belief system, because it threatens naïve rationalizations of the concept of responsible agency by further clarifying the illusionary nature of the feeling of “free will” that coevolved with social systems depending largely on control via communicated abstract meaning. Therefore, crackpots, religious, etc. attack demystifications such as attempted here. Comments are tightly monitored in order to ensure a useful comment section for reasonable readers. Thank you for your understanding.




Comments