I remember, as a child, being very upset by a ventriloquist’s dummy at a show, and crying out and making a ‘scene’.  Even well into my teens and beyond, I felt disturbed by “magic”, even in mathematics or science.  One particular incident I remember was being shown in class the ‘proof’, by an elementary form a calculus of variations, that the shortest path[1] between two coordinates is a straight line.  This left me with an uncomfortable feeling.  That feeling, however, was dispelled when Mary Boas used calculus of variations in the Lagrangian formulation to derive the equation for a particle falling under gravity.  Give me a bit of real maths, elementary though it may be, to drive away any feeling of ‘hocus-pocus’.

Now I had read about two mirrors producing a potentially infinite series of reflections.  This was in a ‘science for young people’ sort of book, and it left me feeling uncomfortable, not only with the thing itself, but with the fact that my reflection in the mirror was ‘really’ back-to-front.  This lingering unease was finally dispelled recently when I started to get to grips with Lie groups.

How come?  Well, here is me getting mixed up with a mirror. 



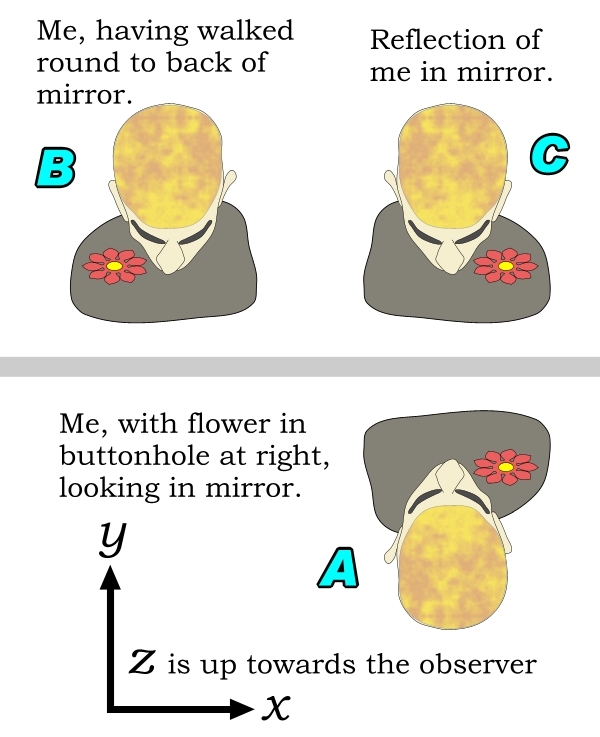
Let us look at the case B where I’ve simply walked round the back of the mirror.  All the coordinates of my head have changed, but if we take the tip of my nose as a moveable origin (0,0,0) then we can treat this as a simple rotation around that origin.

Now an arbitrary rotation involving three Euler angles is represented by this rather hairy matrix.





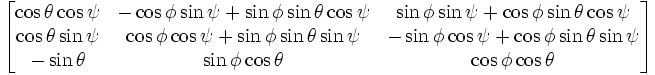
But if I keep my head vertical then it is a simple 180° rotation around the z axis with a much simpler matrix.  Here x and y go negative (left-right and forward-backward are reversed), but z remains the same way up.


 

 


But in my reflection my right button-hole (positive x) is still on the same side.  Only y, forward-backward, is reversed.

 




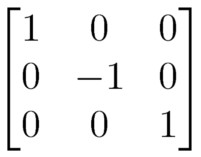So now let’s get to grips with the group theory.  Elements of a group can often be represented by matrices.  But a matrix has to have certain properties to qualify as a member of a given group.



Let us see now how this applies to a simpler system.  Now the fellow on the left here  is the 2-dimensional rotational matrix, representing a rotation about α. 


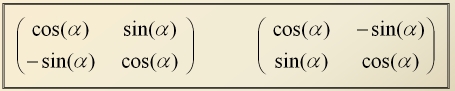
But what’s the fellow on the right?


  • Certainly the two matrices are transposes of each other (the conjugate bit doesn’t apply here, because they’re real.) 


  • Certainly it’s numerically equal to a rotation about – α, so that makes it the inverse.  


  • Applying one matrix then the other, in either order, gives you 1, the identity matrix, or ‘back where you started from’.  


  • So multiplying the either by its (conjugate) transpose gives 1 – both matrices are unitary. 


  • They’re real, so that makes them orthogonal. 


  • Work out their determinant, and either gives cos2α + sin2α = 1, so they’re special.





In other words, they are (representations of) members of the 2-dimensional special orthogonal group, SO(2).  This is beginning to sound a bit particle physics-y.

Similarly, one can show that the 3-dimensional rotation matrix is a representation of the 3-dimensional version, SO(3).

So ,when I walk round the back of the mirror, what is the determinant of my transform matrix?  With matrices where all elements not in the main diagonal are 0, that’s easy – simply multiply all the elements of the diagonal together, and you get 1.  Checking the criteria in the list, one can easily see that the matrix is orthogonal, and special.  It’s a member of SO(3).

But what about the reflection matrix?  Here the diagonal elements multiply to give –1, so the matrix is not special.  It is only a member of O(3).

So while I walk about with a moving origin at the tip of my nose, all the positions of my head are members of SO(3), but me and my reflection in the mirror only relate through O(3).  So we’re not really the same – are we?

Whatever way you choose to answer that question, the group theory has managed to put my mind at rest, for now.

And now that I’ve done all this, I’ve just thought of a much simpler way !!!!!

Want to know what it is?



[1] ‘Path’, not ‘distance’.  The latter is a mistranslation by Carlyle of Lagrange’s French.