Was Hippasus pushed? If you are even mildly interested in the history of mathematics, it is likely that you will have heard something like the following story. The Pythagoreans (who were also into music in a big way) worshipped numbers, and believed them to be the basis of everything. If one were to do a modern caricature of this, it might go:

  Do you believe in Rock ’n’ Roll?
  Can mathematics save your soul?

By numbers, they meant whole numbers or positive integers. Whether this included ‘one’ is a moot point, because later Greek mathematicians regarded ‘one’ as the ‘generator of numbers’. One day, a man called Hippasus discovered that the square root of 2 was irrational. This went so much against the Pythagorean world view that they took him out to sea and threw him overboard. It didn’t stop there, though. The Greeks were so horrified by this discovery that they turned their backs on numbers and started doing everything by geometry instead. In book 2 of Euclid’s Elements they even dressed up quadratic equations in geometrical form, as a kind of Geometric Algebra. To use a Euclidean turn of phrase, I say that this story is both bad history and bad mathematics. Firstly, our knowledge of the Pythagoreans themselves is very muddled to say the least, as the Stanford Encyclopedia of Philosophy shows. Most of it comes from the neo-Pythagoreans, who lived roughly seven centuries later well after the Romans had said to the Greeks “resistance is futile!” Chief among these is Iamblichus, who transmitted five separate inconsistent accounts, chief among which is the following from On the Pythagorean Life:

It is related of Hippasus that he was a Pythagorean, and that, owing to his being the first to publish and describe the sphere from the twelve pentagons, he perished at sea for his impiety, but he received credit for the discovery, though really it all belonged to HIM (for in this way they refer to Pythagoras, and they do not call him by his name).

This would imply that the first incommensurable ratio to be discovered that which an unknown German round about 1830 called the golden section (der Goldener Schnitt) and had earlier been called the divine proportion by the Italian Pacioli in 1509. The Greeks called it the extreme and mean ratio, and Euclid used it in his Elements to construct the pentagon and hence the dodecahedron (the sphere from the twelve pentagons and the basis for the modern soccer ball). There is little evidence, though, that the Greeks used it in architecture. However, a very plausible shot at sorting out this mess was made in 1975 by Wilbur R. Knorr in his book The Evolution of the Euclidean Elements [1], and it is from his book that I draw most of my inspiration for this article. Most other Greek accounts do, however, place the discovery of incommensurability in connection with the side and diagonal of the square, especially references to this in Plato and Aristotle, both of whom lived and worked much closer to the time of Pythagoras. Plato tells us that Theaetetus gave us the general proof of a theorem that if the sum of squares of two numbers is not itself a square number (i.e. a Pythagorean triple) then the diagonal of a rectangle with sides in that ratio is incommensurable with the sides, although we don’t know [2] exactly how he did it. He had developed a proof of his tutor Theodorus for squares on diagonals from 3 to 17. And Theodorus seems to have learnt it from Hippasus. Surviving documents suggest that the Pythagoreans were facing a crisis. Perhaps being viewed with suspicion as a cult by the powers-that-were, they had become refugees. Hippasus suggested making a living by training outsiders in the mathematical mysteries, while Lysis insisted that only those who had undergone the necessary intensive moral training should be admitted to these. What a dilemma!

 Be not righteous over much; neither make yourself over wise:
                 why should you destroy yourself?
 Be not over much wicked, neither be you foolish: 
                 why should you die before your time?

Lysis told Hippasus that if he did not change is ways “you are already dead”. To us, used to gangster movies, this immediately suggests the proverbial “hollow-bottomed boat”, but tradition states that they expelled Hippasus and held a symbolic funeral for him. If he did drown soon after, then all the material for the legend was there. Normally, this “discovery” is taught these days using an algebraic proof which is a bit late 19th century in flavour, relying implicitly on the concept of mutually exclusive sets of even and odd numbers. Now the Pythagoreans were most definitely into the theory of the even and the odd, but they seem to have derived their arithmetical theorems from the use of pebble arithmetic. They would have known that a pebble square of even side could be divided into lots of squares of four pebbles each, while odd-sided squares could be divided into four heteromecic rectangles (yes, that’s their own word!) with a pair of sides which were one greater than the other pair – and this left one space in the middle. But, using our terminology, N(N+1)+2 and N(N+1)+3 would never make a square. 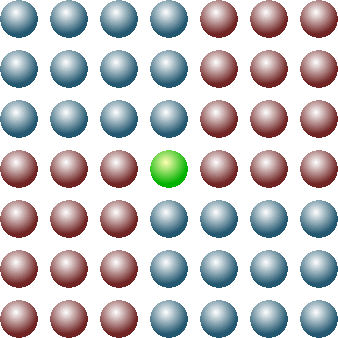With such knowledge, it was straightforward (but by no means easy) for Theodorus and Theaetetus to generalize further. So no need for them to “throw a wobbly” and hide their “algebra” in geometry, as Zeuthen suggested in 1886. Mathematically, the algebraic method would have been totally alien to the early Greeks. The first Greek known to have consistently used symbols was the much later Diophantus, but alas his work did not lead anywhere until it was rediscovered by medieval Arabic and European mathematicians. Because of his use of symbols, he has been called “the father of algebra”, but he was applying them to specific problems. It was the Persian Al-Khwarizmi who first published a general method of putting the “unknown quantity” into the equation, though he did not use a symbolic letter but called it the “thing”. But people do like the modern version of the Hippasus story. Is this because it fits the world-view represented in the film Inherit the Wind and Bertold Brecht’s Galileo? Neither of these is history of science, but it is the latter which I particularly detest. By concentrating on the issue of heliocentrism, it totally clouds the fact that Galileo’s greatest achievement was his mechanics, which in effect married mathematics and physics. Recent followers of this blog will know that tiffs are still occurring in that marriage! Both are also highly political: Brecht was a Marxist, while ItW was Hollywood protest against the attacks of Joseph McCarthy on the acting profession. And in that case there were “Reds under the bed” – it was because of the domination of the actors’ union by communists that Ronald Reagan decided to quit acting and enter politics. But back to nicer things: who agrees with me that the Bird's Nest Olympic Stadium in Beijing is "geometrical poetry"? What would the Greeks have made of that? [1] The Evolution of the Euclidean Elements: A Study of the Theory of Incommensurable Magnitudes and Its Significance for Early Greek Geometry by Wilbur Richard Knorr (Paperback) Kluwer Academic Publishers (Dec 1981) ISBN: 9027711925 [2] http://www.math.harvard.edu/~mazur/preprints/Eva.Nov.20.pdf