Part 2 Some travels through time can be viewed here.
Part 3 discussing language, sequence and order, can be viewed here.
Part 4 a brief discussion of clocks, Steno, Foucault and Allais, can be viewed here.
Note: this blog on time is speculative, not established fact.
A Theory of Time Part 5 : Some Thoughts on Velocity
"the only method to obtain positive knowledge is to leave the incomprehensible unexplained until sooner or later the explanation emerges of its own accord from facts which are so plain that divided opinions about them can scarcely arise. "Wilhelm Ostwald - Nobel Lecture, December 12, 1909
Time as a pattern matching exercise.
In part 4, I wrote: "Objectively, synchronising any two clocks is a process that can be reduced mathematically to the same paradigm as dendrochronology. Time in the abstract is not necessary to the process: it is simply a matter of pattern matching." I shall now show an example of this from everyday experience.
Image three cars, carts or trolleys. Each one carries an inking device, which may be a pen, an ink jet or anything similar. The 'pen down' mechanism in each car is a simple oscillator, balance wheel, or any mechanism with a regular beat, a regular causal chain. The three cars are set in motion on three lines, and each produces a chain of marks. These marks can be plotted on a chart.
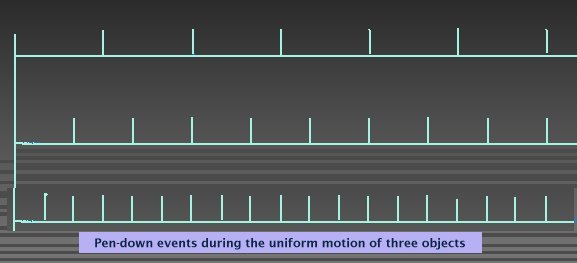
The chart is not marked with units of measure. Such units are entirely arbitrary, an imposition by the mind on the observed data in order to make sense of it. It matters not whether we mark the events as locations along a path in space or as events in time, or even if we leave them entirely unmarked. The outcome is the same: we can determine a relational difference between the three cars.
We note that, when one car has covered a distance which is a multiple of 3, the others have covered the same multiple of 2 and unit distance respectively. The ratio of distances covered is 3:2:1. This is the speed ratio, determined without reference to time as a factor. In all such calculations, if uniform velocity is a factor,we can reduce any calculation to one in which distance substitutes for velocity.
We can express the relational difference in terms of velocity, which seems to imply that time must exist. However, we can also state the relation in terms of comparative distances by notional alignment of - or counting of - pen-down events. Or, rather, by adding up the distances between pen-down events. If we accept the uniformity of the 'clocks', the relative spacings are explained. If we insist that, for each observer, the linear spacings are in some way identical, we must deduce that the 'clocks' are not synchronous. The model also works for pulse events, if we model pulse separations as wavelengths instead of time units. In using an oscilloscope, we commonly measure events in the millimeters of the graticule.
In the case of non-uniform motion, e.g. acceleration, we can still use the same method. In this case, the pen-down events are non-uniform in space, but may still be aligned to derive either an accelerating force or time. If it is accepted that time has no real existence, then a focus on the accelerating force is appropriate.
The N-Body Problem - a suggested heuristic.
The examples of motion along a single vector are easy to calculate. Ultimately, it is a simple tally process. I suggest that, by a stepwise calculation in space rather than in time, the N-body problem has a solution in a heuristic that is reducible to a simple tally.
I shall show how the heuristic is developed by showing a 3-body problem, but the heuristic can be applied to any number of bodies which exert mutual influences.
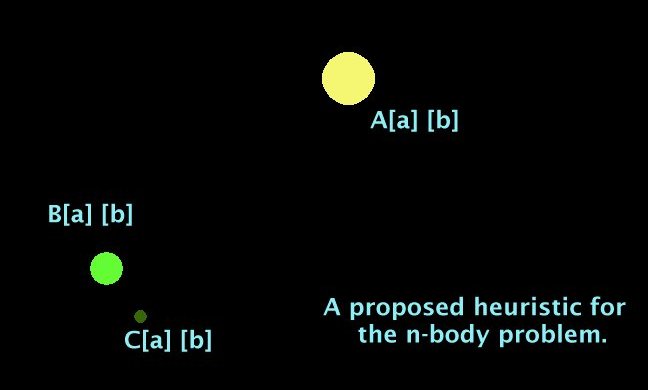
For each object A, B, C ... N we set up two data arrays, A[a][b] B[a][b] ... N[a][b]
In each a array N[a] we store vectors for location, velocity and rotation, and a variable for the mass. By including rotation, we can determine tidal effects between objects. Mass is a variable rather than a constant so that we can model mass loss in radiating bodies as it affects gravitational paths.
The method:
(Note: the following part was edited to correct the omission of the derived ratio vel.)
In implementing the heuristic, we determine an increment of distance, LV for each body, which is the length component of the velocity. The time component is disregarded. For each iteration of the heuristic, we determine the lowest LLv and highest HLv values of LV amongst the data for all of the bodies. We calculate the ratio of HLv to LLv . This fraction, which I shall call a vel is the space-step for that specific iteration. Each body is updated by vel times its local value of LV. The 'space-clock' has no essential uniformity in its 'ticks' - the distance vel ( LV) is different for each location vector of each body and for each iteration. To clarify: vel is calculated once only at the start of each iteration.
For each object, we first increment its location, by applying vel ( LV) to each location vector , in accordance with the data already stored for that object in array N[a]. That increment in spatial vector is stored in array N[b]. We now calculate the resultant of gravitational forces due to the other objects as it affects the velocity of this object, storing the new data in array N[b].
Once we have updated every object's data into its array N[b] we overwrite all arrays N[a] with the respective contents of arrays N[b], and clear N[b].
The process is repeated through as many iterations as may be required.
The accuracy of the model may be refined by using a constant fraction applied to vel, thus making the update increments smaller. All dimensions of velocity in the model are measured in linear distance along a vector per program-step. The program-steps substitute for the time dimension. Instead of 'time-slicing' the problem, we 'space-slice' it. The time slices are by definition constant. The space slice fraction vel is re-evaluated after ever iteration of the heuristic. It is an emergent value in the process which is being modelled.
By using the vel as a 'clock' unit, the speed of processing becomes independent of overall velocity changes within broad limits. If a constant unit such as the meter, kilometer etc were used for the steps, the model would become ever more inacurate, due to the increased coarseness of detail with velocity. If a unit of time were used, an update by dimensions in space would take ever-increasing time to compute with increasing velocities.
Discussion: since I am a programmer rather than a mathematician, I am unable to reduce this model to a mathematical function. I am therefore not able to 'prove' the concept in the mathematical sense.
I welcome all comments. If there is an error in my approach, I would be glad to know of it.
This blog is continued in Part 6.



Comments