Yet the laws of physics tell us that when studying the evolution of physical systems in all its microscopic details, there is no preferred 'direction of time'. The fundamental laws of physics obey time symmetry. For every forward evolution there exists a time reversed evolution. Both evolutions are equally valid and equally likely. Reverse all velocities in Newton's dynamics and the system traces back its history.
The laws of physics tell us that forward and reverse directions of time are absolutely indistinguishable down to the minute and microscopic details. Yet, we all know that when we are watching a movie we can quickly tell whether the movie is displayed in reverse or not. We seem to have manouvred ourselves in a paradoxial situation.

Enter Ludwig Boltzmann, the posthumously famous Austrian physicist who was tragically ahead of his time and - following many years of struggle to get his ideas accepted by the scientific establishment - died by suicide in 1906. Boltzmann left a legacy that is now much better understood. He provided us with the guidance and the tools to marry the time-reversible laws of physics with the time-irreversible behavior we observe in our everyday world.
At the heart of Boltzmann's theories is a statistical approach towards the description of nature. In particular, Boltzmann showed that the thermodynamic entropy of a system, the amount of energy no longer available to do physical work, can be defined rigorously in a statistical way. In simple terms, Boltzmann's entropy S is the minimum length of the encoding you need to fully describe the state of the system. It is the amount of info (number of bits or digits) you need to trace back the history of the system.
The following 'Fibonacci fleas model' should make this more concrete.
Consider a dozen fleas feeding on nine cats (targets labeled '1-9') and a human (target '0'). At discrete intervals, the fleas jump from one target to the other according to a sequence of 12 digit integers being generated. These integers represent the states of our discrete dynamic model by enumerating the locations of the fleas. For instance,
504,328,976,279
means flea number 1 is located on cat 5, flea 2 can be found on human 0, flea three on cat 4, and so on up till flea 12 who is located on cat 9. If the next state is
432,522,910,327
we observe a synchronized jump with the first flea jump from cat 5 to cat 4, the second flea from the human to cat 3, etc.
The generation of these integers in this discrete model follows a simple time-symmetric mechanics: based on the last two numbers generated, the next number is three times the last minus the one-but-last. If the number computed exceeds 999,999,999,999 or becomes negative, it is mapped into a 12-digit positive integer by adding or subtracting the appropriate multiples of 1,000,000,000,000. So referring to the number generated at timestep t as W(t), we have:
W(t+1) = 3 W(t) – W(t-1) (mod 1,000,000,000,000)
It is important to stress at this point that the dynamics is indeed time-symmetric as this equation can also be written as:
W(t-1) = 3 W(t) – W(t+1) (mod 1,000,000,000,000).
Starting from W(0) = 0 and W(1) = 1, this reversible arithmetic in forward mode yields the even Fibonacci numbers:
0, 1, 3, 8, 21, 55, ...
whilst the odd fibonacci numbers are generated when starting from W(0) = 1 and W(1) = 1:
1, 1, 2, 5, 13, 34, 89, ...
Let's start with the latter initial condition, and see what happens to the distribution of fleas. We write the full 12 digit numbers so as to make explicit the location of each flea. We observe:
W(0) = 000,000,000,001
W(1) = 000,000,000,001
W(2) = 000,000,000,002
W(3) = 000,000,000,005
W(4) = 000,000,000,013
W(5) = 000,000,000,034
W(6) = 000,000,000,089
W(7) = 000,000,000,233
and so on. We can now track the total number of fleas on the human (the number of zeros in the 12-digit numbers) Obviously, starting at t = 0 with all the fleas on the human (twelve zero's), the number of fleas on the human gradually decreases. This trend continues untill after 28 steps a state is reached that has no fleas on the human:
W(28) = 139,583,862,445
From that moment on the number of fleas on the human fluctuates around values close to zero:
W(29) = 365,435,296,162 (no fleas bothering the human)
W(30) = 956,722,026,041 (two fleas)
W(31) = 504,730,781,961 (two fleas)
etc.
Let us now focus on the entropy of this flea dynamics. Recall that we defined entropy as the minimum number of digits needed to re-trace the system's history. To be able to do this, one needs just the last two flea-state numbers. Using these two numbers we compute all preceding numbers simply by applying the same dynamics in reverse direction (second equation above).
So what does this tell us about the entropy S?
Having reached state 29, retracing the history requires the two full 12-digit numbers W(29) and W(28) or an entropy of 24 digits. The same is true once the dynamics has brought us beyond t = 29. However, when the dynamics has evolved no further than some earlier time, this is no longer true. As an example, consider the evolution to t = 7. We need the two numbers W(6) and W(7) to retrace the full history. So that is again two times twelve digits, right? Wrong. You only need a total of 6 digits (S = 6) as ignoring the leading zero's (which are irrelevant for computing the dynamics) both numbers have only three digits.
Carefully counting the number of digits in subsequent pairs of W-numbers whilst ignoring the leading zero's, we observe the entropy to increase to its maximum value S = 24 digits in about 28 timesteps (see figure). Now this is interesting. The irreversibility paradox manifests itself in its full glory in this simple fleas model. Using nothing more than a very simple fully time symmetric Fibonacci-type dynamics, we observe an 'arrow of time' in the form of an entropy that increases in one direction, and decreases in the reverse direction.
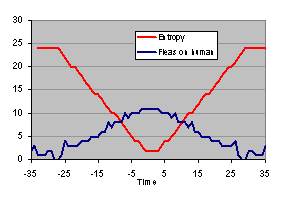
It should now be clear what is causing the entropy increase with time. Entropy increases simply because te system started in a specially prepared low-entropy starting state. There is no paradox related to the fact that the dynamics is reversible. This can be observed more clearly by continuing the reverse dynamics into negative times. This results into a perfectly time-symmetrical plot of entropy (red curve) and number of fleas on the human (blue curve).
In his superb book “The Emperor's New Mind” Roger Penrose takes this reasoning further and applies it to the universe and its origin. He stresses the fact that the universe started off at what he refers to as a 'ridiculously tiny entropy' state. Based on a closed universe model (a universe that eventually collapses into a big crunch) and some holographic considerations, he comes to the conclusion that the creator had to select some 10^123 digits each to a unique value such as to create a universe with the known low entropy as we witness it today.
In other words, only one out of 10^(10^123) possible initial universes had the right properties for the universe to evolve with a second law of thermodynamics as powerful in effect as in our universe. These are no mind boggling figures. These numbers are simply incomprehensible. In a future blog I will revisit this issue and present you with a simple model for an expanding universe that in terms of entropy behaves in a remarkably different way.




Comments