The earth being round, the atomistic nature of matter, our unremarkable place in the universe, and us being a product of evolution, all being examples of such insights. Other insights, although unanimously embraced by experts, have a long way to go for a larger population to accept them. More than for any other subject, this holds for quantum physics. No other product of human thought is as profoundly mysterious as quantum theory.
Unfortunately, the subject is not easy to digest and, to make things worse, it is often misrepresented in the pop-science literature. Those eager to understand the quantum are often fed with confusing slogans and misleading analogies.
A year ago I dedicated two blogposts (here and here) to the mysteries of the quantum. Judging from the reactions, these posts must have been useful to at least a few of the readers. The simple thought experiment presented (dealing with Albert's socks) allows the reader to explore the weird world of quantum physics, an experience that likely will challenge the reader's view on reality. A view that - for all of us - is heavily biased by sensory perceptions limited to classical (non-quantum) physics.
Yet, I feel one question remained insufficiently discussed in my earlier posts. And that is the question how physicists deal with quantum reality. Let's see if I can fill this gap by further exploring Albert's quantum socks.
ALBERT'S SOCKS
 Albert's chest of quantum drawers, although most spooky in its behaviors, appears rather unremarkable and featureless from the outside. Three rows, each consisting of three drawers, make up this piece of furniture. Each night, when Albert is sound asleep, his housekeeper fills this cabinet with fresh socks. The next morning, whenever Albert pulls open a drawer, he is presented either with a single sock or an empty drawer. Unfortunately for Albert, he can not open just any number of drawers. Each morning, his search for fresh socks is limited to the opening of three drawers: any three drawers forming a horizontal row or any three drawers forming a vertical column.
Albert's chest of quantum drawers, although most spooky in its behaviors, appears rather unremarkable and featureless from the outside. Three rows, each consisting of three drawers, make up this piece of furniture. Each night, when Albert is sound asleep, his housekeeper fills this cabinet with fresh socks. The next morning, whenever Albert pulls open a drawer, he is presented either with a single sock or an empty drawer. Unfortunately for Albert, he can not open just any number of drawers. Each morning, his search for fresh socks is limited to the opening of three drawers: any three drawers forming a horizontal row or any three drawers forming a vertical column. Initially, out of habit, each morning Albert opens a horizontal row of drawers. He does this without giving much thought to which of the three rows to open. After a few days, he starts noticing a pattern. Whichever row he opens, either all three drawers are empty, or two drawers each contain a sock leaving one empty drawer. In other words, a row of drawers always contains a total even number of socks. Many days pass by, and Albert never encounters a row not containing an even number. That makes sense: each row containing an even number of socks tells Albert that each morning the chest must be filled with an even number of socks. An observation comfortably compatible with the notion that socks come in pairs.
One morning, Albert decides to deviate from his fixed ritual, and he opens a vertical column of drawers: the three leftmost drawers. Interestingly, this time he observes an odd number of socks distributed over the three drawers opened. The next day, he opens the same leftmost column of drawers, and again observed an odd number of socks.
Albert gets curious about the other columns. What number of socks will they reveal? The next morning he opens the middle column. Again an odd number of socks. The next day he once more checks the middle column. Once again he observes an odd number of socks.
Albert is a clever guy, and he now realizes he can predict with certainty that the rightmost column of drawers must behave differently from the two columns already inspected. The rightmost drawers for sure must contain a total number of socks that is even. This is obvious as an odd number of socks in the rightmost drawers, added to the number of socks in the middle column (observed to be odd) and the leftmost column (also observed to be odd) would result in an odd total number of socks in the chest. A contradiction, as he had already observed, based on opening horizontal rows, that the total number of socks in the chest is always even.
The next morning he eagerly opens the three rightmost drawers. To his astonishment he observes an odd number of socks.
The next few mornings he randomly checks the various columns. Each attempt reveals an odd number of socks. Albert realizes something must have gone wrong. Maybe his housekeeper coincidently changed from filling the chest with an even number of socks to filling it with an odd number of socks, just at the time he switched over from opening horizontal rows to vertical columns?The next morning Albert again opens a horizontal row. An even number of socks stares him in the face. He starts randomly switching between horizontal rows and vertical columns. Horizontal rows always deliver even numbers, vertical columns odd numbers.
This drives Albert crazy. The results he is obtaining are logically impossible. "At any given morning if I would open three rows", Albert reasons, "I would end up with an even number of socks. However, would I open three columns, I would end up with an odd number of socks. Yet in both cases I would have opened the same nine drawers. How can this be?"
SHUT UP AND CALCULATE!
"Nice story" you might react, "but nothing more than a fantasy. Obviously chests of drawers like these logically can't exist in our world".
Well, as a matter of fact, they do. I can put that even more strongly: all evidence points at our world consisting solely of devices like Albert's drawers. It just happens to be that these drawers tend to be very, very small and that we generally observe the aggregate behavior of many drawers without being able to distinguish critical details such as the distinction between even and odd counts.
Many physicists deal with quantum reality day in, day out. How have they come to terms with a physical reality that presents us with devices like Albert's chest of drawers? Physicists don't seem to lose any sleep over the many counter-intuitive notions and apparent paradoxes surrounding quantum theory. Are they oblivious to the utterly strange world view that the quantum represents?
Not at all. The point is that the vast majority of physicists simply have stopped worrying and have embraced a practical approach described by the catch-phrase:
"Shut up and calculate!"
 This phrase was coined by Cornell physicist and science communicator David Mermin, in an attempt to mock the widely-accepted Copenhagen interpretation of quantum physics. Mermin was not at ease with the Copenhagen position put forward by Niels Bohr in the famous Bohr-Einstein debates. Ironically, two things happened following the publication of Mermin's phrase. Firstly, Mermin's own ideas on how to interpret quantum physics started to converge towards the Copenhagen interpretation. Secondly, the "shut up and calculate" phrase achieved the status of a popular instrumentalist approach to quantum physics equated with eschewing all interpretation.
This phrase was coined by Cornell physicist and science communicator David Mermin, in an attempt to mock the widely-accepted Copenhagen interpretation of quantum physics. Mermin was not at ease with the Copenhagen position put forward by Niels Bohr in the famous Bohr-Einstein debates. Ironically, two things happened following the publication of Mermin's phrase. Firstly, Mermin's own ideas on how to interpret quantum physics started to converge towards the Copenhagen interpretation. Secondly, the "shut up and calculate" phrase achieved the status of a popular instrumentalist approach to quantum physics equated with eschewing all interpretation.Let me try to offer you the "shut up and calculate" approach as a choice for coming to terms with the quantum. To do that, I need to explain how to calculate sock counts for Albert's drawers.
LOADED DICE
The mathematical machinery behind quantum devices like Albert's chest is compelling and carries a great beauty. It is based on a generalized probabilistics that adds likelihoods not as a linear sum, but rather as a Pythagorean sum. I would love to present this quantum math to you. But alas, the math is too involved to explain in a blog like this.
Fortunately, the complex quantum math built on Pythagorean sums can be mapped on the much simpler classical math based on straightforward linear sums. Physicists apply such mappings all the time when studying what is known as "the classical limit" of quantum systems: the behavior of large quantum systems that can be accurately represented with classical (non-quantum) laws of physics.
Eugene Wigner, one of the quantum pioneers, discovered in the early 1930's that something weird happens when approximating quantum physics with classical probabilities. He discovered that one can describe quantum systems with probabilities that add linearly, but these probabilities are no longer guaranteed to be non-negative.
Paul Dirac, Wigner's brother in law, later wrote a paper that discusses the use of concepts like negative energies and negative probabilities in quantum physics:
"Negative energies and probabilities should not be considered as nonsense. They are well-defined concepts mathematically, like a negative of money."
Years later the idea of negative probabilities received increased attention when Richard Feynman started to popularize the idea:
“Trying to think of negative probabilities gave me a cultural shock at first, but when I finally got easy with the concept I wrote myself a note so I wouldn’t forget my thoughts. . ."
In describing Albert's chest of drawers, how far do we get with negative probabilities? Before you read my negative probabilities description for Albert's chest, I urge you to try it yourself first. It's a straightforward and instructive exercise.
Ok, here is a probabilistic description of Albert's drawers. A total of 10 configurations are relevant:
Ok, here is a probabilistic description of Albert's drawers. A total of 10 configurations are relevant:
1) Nine configurations consist of two drawers in a single row being filled, and all other drawers being empty. These nine configurations each carry a 1/6 probability.
2) One additional configuration features an empty chest of drawers. This configuration carries a minus 1/2 probability.
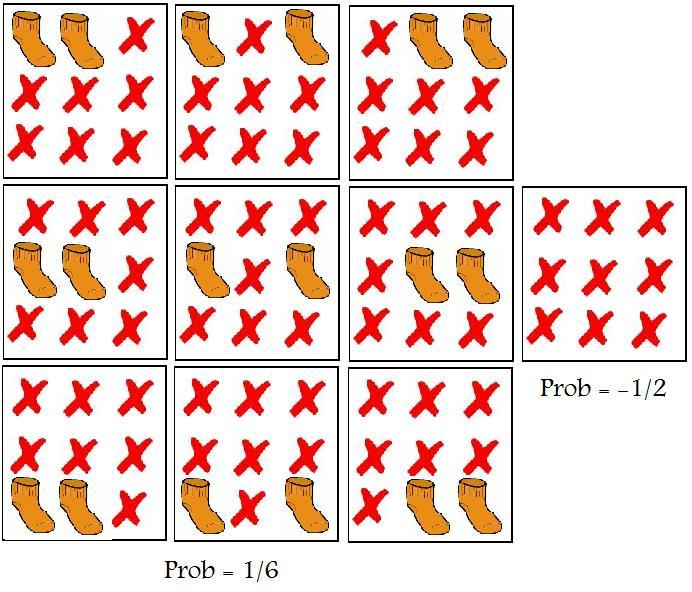
It is easy to see that all probabilities add up to unity, as they should. The negative probability for the 'all empty' state is a strange beast, but a beast that doesn't show up in the end result when calculating observable probabilities.
For instance, let's calculate the probabilities for observing the various numbers of socks in the bottom row of Albert's chest. In the above table you can read off that we have seven realizations with an empty bottom row, six with +1/6 probability, and one with -1/2 probability. The total probability for an empty bottom row is therefore +1/2. Furthermore, we have three realizations with a bottom row filled with two socks, each with a probability of +1/6. The total probability for finding two socks in the bottom row is therefore +1/2. So we have two equal likelihoods of finding zero or two socks, each with a positive (+1/2) value, and we are guaranteed to retrieve an even number of socks from the bottom row.
Repeating the same calculation for a column leads to the result that a column renders one sock with unit probability, hence a guarantee for an outcome of an odd number of socks.
What happened in both these cases is that the negative probability gets cancelled by positive probabilities describing the same outcome for the row or column under consideration. As a result, rows lead to even numbers and columns to odd numbers, and never does a negative probability turn up its ugly head.
This obviously doesn't hold when determining the number of socks in the entire chest of drawers. A negative probability does show up prominently, and it does not get cancelled as there are no positive probabilities describing the same configuration. However, we don't need to worry about this, as the configuration with negative probability does not correspond to a possible observation. Only three drawers (one row or one column) can be opened, not the whole chest.
What this means is that one can extract only a limited amount of information out of Albert's chest. Getting more information out of it (opening more drawers) is impossible as it would lead to negative probabilities to become evident. This is a manifestation of Heisenberg's uncertainty principle for Albert's chest.
Heisenberg uncertainty, destructive interference, spooky action at a distance, violation of Bell's inequalities, all of quantum physics can be mapped on negative probability models. So why don't physicists use such negative probability models? The answer is simple: negative probability models are rather clumsy representations of what is better described using "Pythagorean probabilities".
But as a model to get some understanding of the fundamentals of quantum physics, negative probability models do carry a value largely unexplored by pop-science writers.
All of this places some of Einstein's quotes in a different light.
God does play dice. And malicious he is. Or how would you characterize anyone who throws dice loaded to render negative chances, and who manages to keep this so well-hidden from us?





Comments