A recent paper makes a connection between the quantum group SLq(2), which describes knots, and the elementary particles of the Standard Model. A mathematical knot is an embedding of a circle in 3-dimensional Euclidean space. Unlike your shoes, with their knot
the ends are joined together so it cannot be undone. The Standard Model, created in the 1970s, is the dominant hypothesis concerning electromagnetic, weak, and strong nuclear interactions in fundamental particles.
Some suggest that leptons, neutrinos, and quarks might be composite and the authors seeks to make the case that the structure is described by the quantum group SLq(2).
The elements of the fundamental (j = 1/2) representation of SLq(2) are interpreted as creation operators for preons. The preons interact through a preonic vector field defined by elements of the adjoint (j = 1) representation.
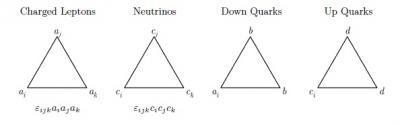
Three-preon structures for charged leptons, neutrinos, down quarks, and up quarks. Credit: World Scientific
The leptons and quarks then appear (as required by the electroweak data) as elements of the j = 3/2 representation. Unexpectedly the electroweak quantum numbers of the so defined preons, leptons, and quarks agree with the corresponding quantum numbers of the elementary constituents conjectured earlier by Harari and Shupe.
In the schematic figure displayed above the leptons and quarks are composed of preons (a, b, c, d) as shown a, b, c, d are the elements of the fundamental representation of the SLq(2) a_i and c_i are also elements of the fundamental representation of SU(3).
In this SLq(2) extension of the Standard Model, the field operators of the standard model are renormalized by knot factors which are representations of SLq(2), and the couplings of the standard model Lagrangian are thereby modified by SLq(2) form factors. A similar development leads to a Lagrangian for preons.
Since the SLq(2) extension of the standard model describes a finer level of structure than the standard model, there are many open problems, including questions concerning gravitational binding, the existence of free preons, and the renormalization of the Lagrangian dynamics.





Comments