That means some day you could have a golf ball optimized for your swing.
Fluid flow optimization is nothing new, if you could download NASTRAN 25 years ago you could simulate parts of planes, trains and automobiles - or even golf balls - but we all basically fly and drive within the same parameters and very few of us swing a golf club the same way. And golf balls are not like other things. In a car you want a smooth line and an even profile - in golf balls those things make balls travel less distance.
It's no secret that dimples improve the flight of a golf ball. Once in flight, a golf ball experiences aerodynamic forces generated from the surrounding air flow as well as gravity. The latter constantly pulls it towards the ground, while the aerodynamic force in the direction of motion, or drag force, dictates the distance it travels. The main purpose of dimples is to reduce the drag and help the ball fly farther. Actually, dimpled golf balls experience about half the drag as those with no dimples.
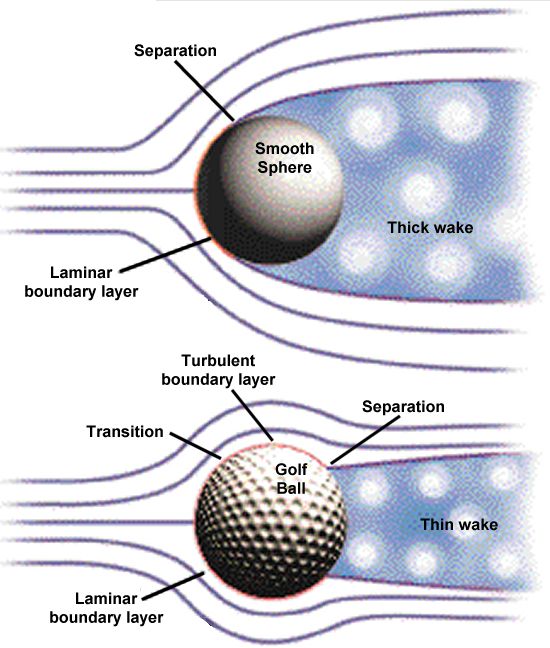
Laminar versus turbulent boundary layer flow separation with and without dimples. Courtesy: TopFlite.
Although the United States Golf Association (USGA) regulates the design of golfballs, laying out uniform size and weight specifications that all approved golf balls must meet, the dimple pattern is not regulated. It is one of the very few parts of the ball over which companies have freedom to change the design. But what pattern is best for lowering the drag?
Dimple design has always been more of an art than a science. Sporting goods companies design their dimple with some modeling but the actual patterns are more trial and error, testing prototype after prototype against one another. The new study takes a different approach, asking how to design dimple size and pattern based on mathematical equations that model the physics of a golf ball in flight. Working out the solution to these equations -- even on the fastest personal computers today -- is not feasible since it would take more than 15 years of computing time just to get a glimpse of the flow around the golf ball for a fraction of a second.
"For a golf ball, drag reduction means that the ball flies farther," says ASU's Clinton Smith, a Ph.D. student who presened a talk on the research on Sunday, November 23, 2008 in San Antonio. Smith and his advisor Kyle Squires conducted in collaboration with Nikolaos Beratlis and Elias Balaras at the University of Maryland and Masaya Tsunoda of Sumitomo Rubber Industries, Ltd.
Beratlis, a Ph.D. student at the University of Maryland, and his advisor Balaras have been developing highly efficient algorithms and software to solve these equations on parallel supercomputers, which can reduce the simulation time to the order of hours. The number crunching for a typical computation, for example, takes approximately 300 hours using 500 fast processors running in parallel (normal desktop computers may have one or two slower processors).
The group's work presented by Smith in San Antonio will summarize their research. So far, they have characterized air flow around a golf ball at the finest level of detail ever attempted, teasing out the drag at each exact location and showing how air flows in an out of each tiny dimple on a golf ball's surface as it spins through the air during flight.
In the end, they produced a model that reveals the physics of a flying golf ball with the greatest level of detail ever seen -- the first step in achieving the project's long-term goal of optimizing dimple design to realize the lowest drag possible. The next step, says Smith, is to extend the work by comparing different dimple designs.
The talk, "Direct Numerical Simulations of the Flow around a Golf Ball: Effect of Rotation" was on Sunday, November 23, 2008. Abstract: http://meetings.aps.org/Meeting/DFD08/Event/90118






Comments