Patrick Draper is a graduate student in physics at the University of Chicago and Argonne National Lab. He is a native of Illinois and lives in Hyde Park, Chicago with his wife Karen and parrot Felix, to whom he is grateful for their love, patience, and correcting his sign errors. He is a supporter of the international effort to put a muon collider on Mars, and is waiting for NASA to return his phone calls.
I asked Patrick to write here about his studies on the discovery reach for a MSSM Higgs boson after I saw his paper on the arxiv a month ago, and am now glad I did. Enjoy!

First, I would like to thank Tommaso for this opportunity to write here about the questions my collaborators and I have been studying on Higgs physics at the Tevatron. As readers of his blog are no doubt aware, there has been considerable interest lately in the potential for the Tevatron collider to exclude or provide evidence for the Standard Model (SM) Higgs boson at a statistical significance of 2-3σ. This capacity is sensitive to the Higgs mass, which governs its decay rates into detectable SM particles, as well as experimental parameters such as the total amount of data they will collect and the efficiency of extracting the signal events. The Tevatron may run for a couple more years, which would allow the CDF and DZero experiments to obtain around 10fb^-1 of data apiece. Furthermore, the analyses continue to improve, motivating an investigation into how much improvement and data are necessary in order to place limits on the SM Higgs.

On the other hand, the SM might not be the end of the story. TeV-scale supersymmetry is an attractive extension of the SM which provides a natural dark matter candidate, a technical solution to the hierarchy problem, and gauge coupling unification. It is useful to consider the Tevatron reach for the Higgs sector of the minimal supersymmetric extension of the Standard Model (MSSM), which differs from that of the SM.

In our recent paper (arXiv:0905.4721), Tao Liu, Carlos Wagner, and I studied these questions and placed conservative upper limits on the improvements in signal efficiency necessary for the Tevatron to probe significant fractions of both the SM and the MSSM Higgs parameter space. Here I will review some of our methods and findings.

Let us start off with the SM. The constraints presented by the experimental collaborations are typically phrased as upper bounds on the amount of signal that could be coming from a particular detection channel, normalized to the signal predicted by the SM in that channel, for each possible value of the Higgs mass. This upper bound is called R⁹⁵ (95 because the limit is typically set at the 95% confidence level), and an example of the limits from CDF for a number of different channels is reproduced below:


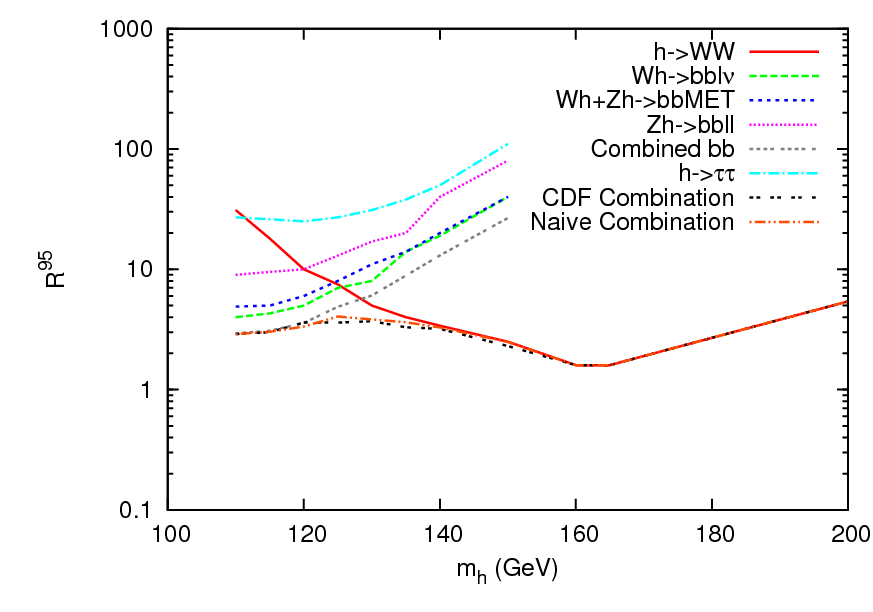
There are two main things to understand about this figure. The first is that anywhere the curves go below 1, a SM Higgs with that mass is excluded at 95% C.L. This does not happen anywhere in this plot, and indeed CDF alone has not made any exclusions on the SM Higgs. The other thing to notice is the the black and orange curves. The black curve is the exclusion limit CDF achieved by statistically combining the limits from all of their individual search channels (if your experiment tells you that you are 90% sure the Higgs is not at 150 GeV, and another independent experiment comes along and says it is 90% sure the Higgs isn't at 150 GeV, then taken together you are now more than 90% confident- it is as if you took more data on your own experiment.) However, the exact formula for the combination of channels is rather complicated (you can see the formula as well as the source for this plot here) and for our purpose it is useful to have a simpler but still reasonably accurate way of combining the limits from different channels. We will assume that the upper limits are governed only by statistical errors, and then they can be combined as 1/R²_combined = Σ_i 1/R²_i, where the sum runs over the channels i. The orange curve gives this combination, and it gives a good, slightly conservative match to the black line.

Furthermore, all the CDF channels can be combined with all the limits from DZero to give the strongest limit available from the Tevatron. This was done in March of 2009 and resulted in an exclusion of the SM Higgs between 160-170 GeV, as discussed on this blog.

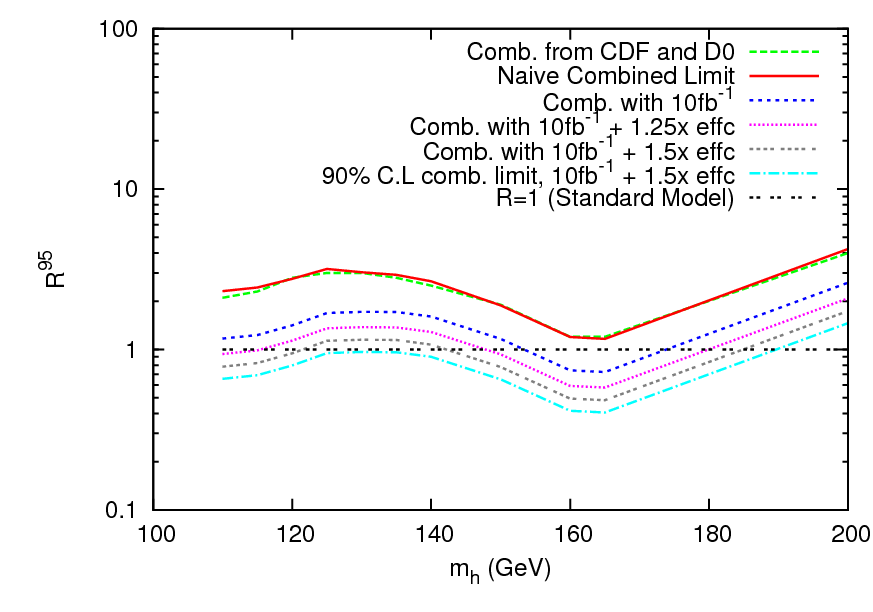
The naive combination of limits scales as the inverse of the square root of the total luminosity, and as the inverse of the signal efficiency- it is better to improve the extraction of the signal than to simply take more data. In the figure below we have plotted the combined CDF+DZero limit, the combined limit from the simplified formula, and projections for the ranges of Higgs masses that could be excluded at 90 or 95% assuming 10 fb^-1 per channel for a variety of improvements in the signal efficiency. The limits for other values of efficiency and luminosity can be estimated from this plot: for example, the difference between 7 and 10 fb^-1 is approximately the same as going down a step in signal efficiency curves. Also note that on this plot the range 160-170 GeV is not excluded by the current combination. This is because this plot presents the expected limits; the real data exhibited a fluctuation that allowed for a stronger exclusion. Since we cannot count on another downward fluctuation in the future, projections have to be made with the expected limits.

Now we would like to take these limits and translate them into limits on the larger parameter space of the CP-conserving MSSM Higgs sector. The MSSM contains two Higgs complex doublets H_d and H_u, giving rise to three physical massive Higgs particles. Two are even under CP and are denoted h and H by order of their masses, and one is odd, denoted A. When considering the constraint from a particular search channel, we must allow for the possibility that any accessible Higgs state is created.

At tree level, there are only two inputs to the Higgs sector. One can be taken to be the mass of the CP-odd scalar, m_A, and the other is the ratio of the vacuum expectation values of the neutral components of H_u and H_d, denoted tan β=H_u⁰/H_d⁰ (this just tells you which Higgs is pulling more weight in terms of giving mass to the W and Z gauge bosons). Typically, over the (m_A, tan β) plane, one Higgs has couplings to the W and Z that are SM-like, and the other has non-standard, highly-suppressed gauge couplings. The couplings of h and H to fermions also differ from those of the SM Higgs. Therefore, the limits obtained on the SM Higgs have to be rescaled at each point in parameter space to correct for the difference in MSSM Higgs production and decay rate relative to the SM.

When the leading quantum corrections are included, a few more parameters of the MSSM have to be specified, and the properties of the physical Higgs particles can be altered. To simplify the parameter space, a handful of benchmark scenarios were developed in hep-ph/0202167 which assign fixed values to all of the parameters except m_A and tan β. These scenarios were chosen to demonstrate interesting and representative distinct features of the radiative corrections.

For brevity I will only survey the projected limits that come from a combination of SM-like search channels, i.e. ones that involve a W or Z either in the production of a Higgs or in its decay. (In the paper we discuss other searches which are targeted towards detecting the nonstandard Higgs whose couplings to these gauge bosons are suppressed, and the combination of this limit with the SM-like one.)

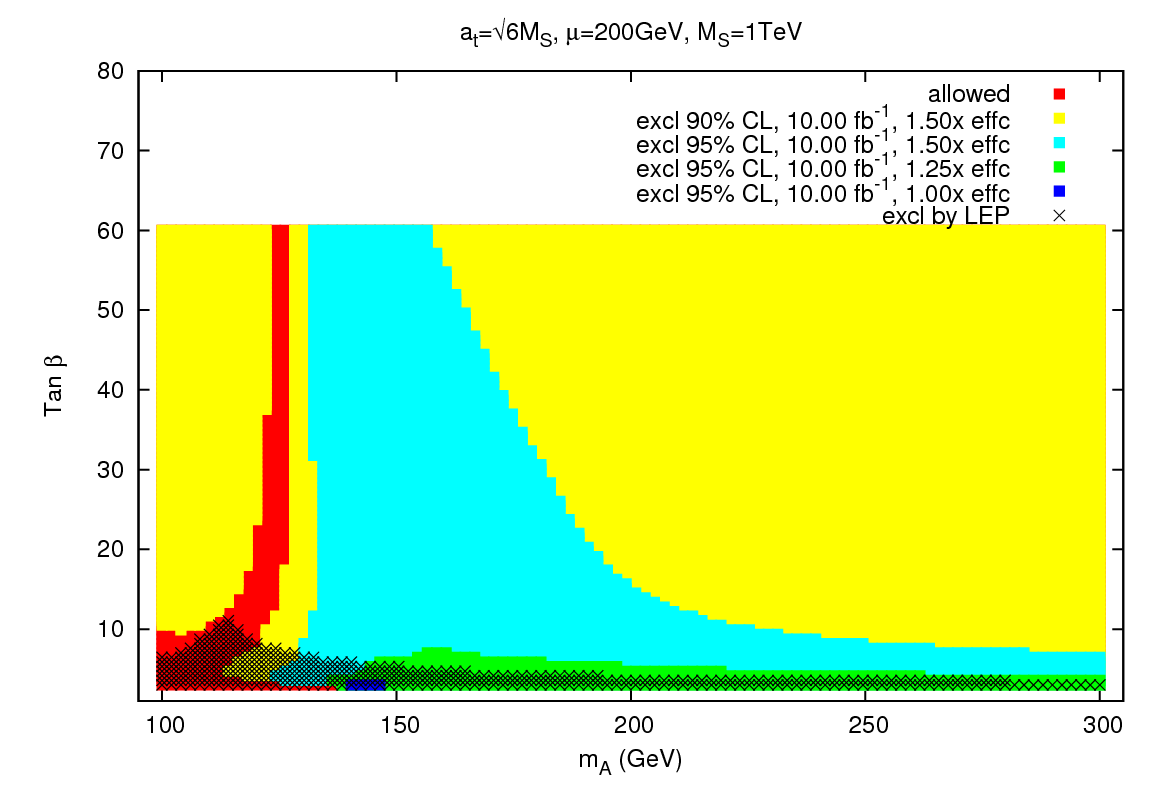
The first benchmark scenario is known as "Maximal Mixing," where the radiative corrections are chosen to maximize the lightest Higgs mass m_h. This is interesting because without large radiative corrections, the lightest MSSM Higgs would have been observed already at LEP. The upper bound on m_h is about 125GeV in this scenario, which occurs for large m_A and tan β, a region known as the "decoupling limit" because H becomes very weakly coupled to SM gauge bosons and h obtains the couplings of the SM Higgs.

The figure below presents our projections for the regions of Maximal Mixing parameter space which may be excluded or probed at 90 and 95% C.L., for the same set of efficiency improvements and luminosity as in the SM case above. Our results indicate that with 50% signal efficiency improvements it is possible for the Tevatron to reach a large section of the parameter space, but the decoupling limit can be probed only at 90% statistical significance. The reason for this can be seen from the SM plots above: for an SM Higgs mass around 125 GeV, the constraint is weakest. At lower m_A and tan β, the light Higgs mass is lower and its branching ratio to bottom quarks is enhanced, leading to a stronger constraint from those channels. For very low m_A, we reach the "anti-decoupling limit," where the light Higgs decouples from SM gauge bosons, while the heavy Higgs H becomes very SM-like and has a mass around 126 GeV. Therefore, in this region the constraint is coming entirely from the production and decay of H instead of h.

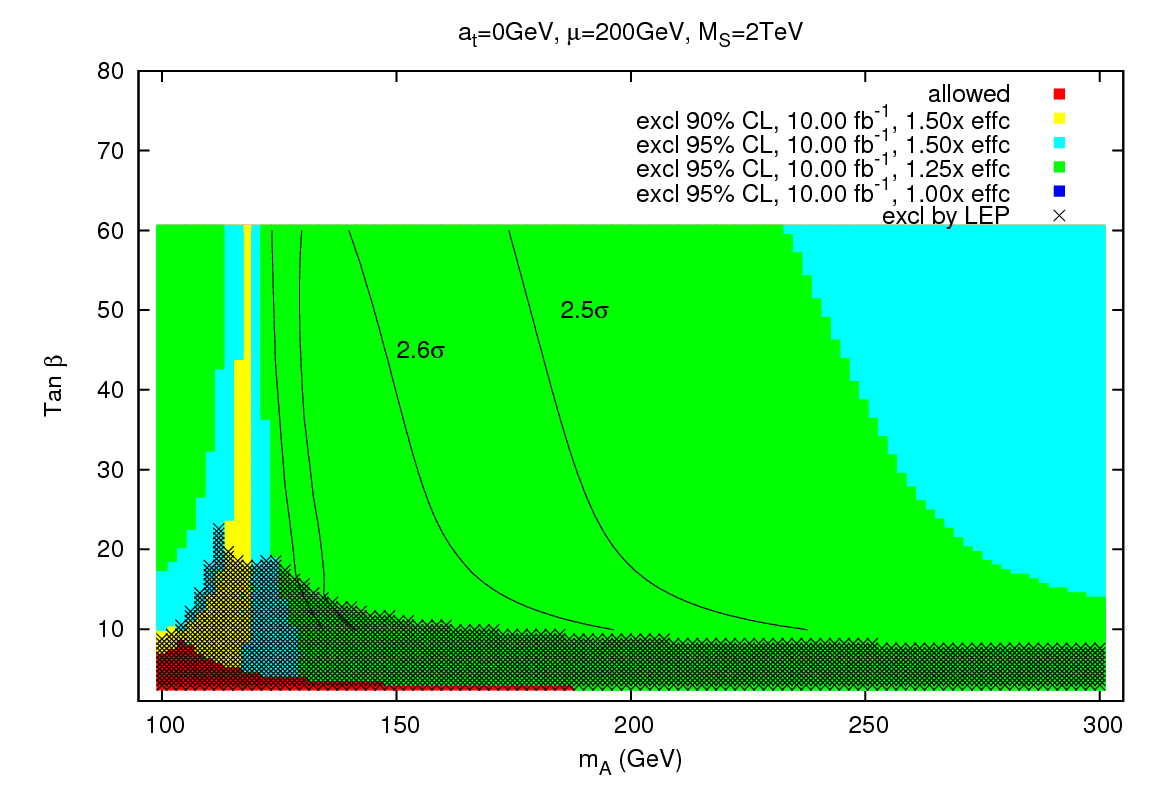
The second scenario, known as "Minimal Mixing," is a set of theoretically well-motivated parameter values which lead to a lightest Higgs mass just outside the current experimental lower limits, around m_h~117 GeV. This scenario is also appealing because the lower masses imply that it can be reached more easily at the Tevatron. As in the Maximal Mixing case, the plot below presents the projected regions where limits may be set. The green region can be reached at 95 %C.L. with only a 25% efficiency improvement, but we also provide contours showing the level of statistical significance that can be achieved with the full 50% improvement.


A third scenario is called "Small-α_eff" and demonstrates potential limitations of relying on the typical low-mass SM Higgs decay mode, h->bb. In this scenario, the b quark decay mode is strongly suppressed for a significant window of m_A and tan β, and so it is necessary to consider the utility of typically subdominant decay modes such as h->WW. Typically the light Higgs has a low WW branching fraction, around 15%, but the bb suppression leads to an enhancement of the WW branching up to about 50%. The first figure below contains the constraints in this scenario from just the h->bb channel. There is a significant red region which is inaccessible even with luminosity and efficiency improvements, due the reduction in the hbb coupling. The second figure contains the combined h->bb and h->WW constraints, and it is clear from the decrease in the red regions that the latter channel can make a significant contribution.





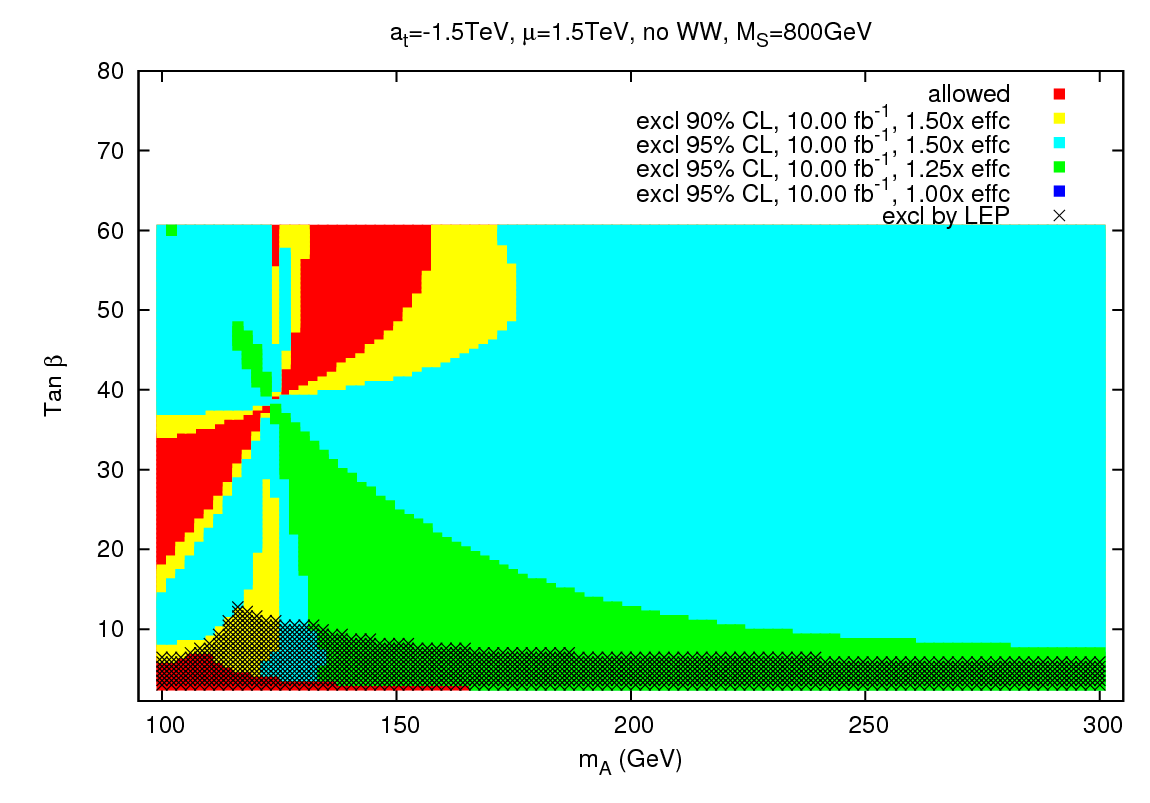
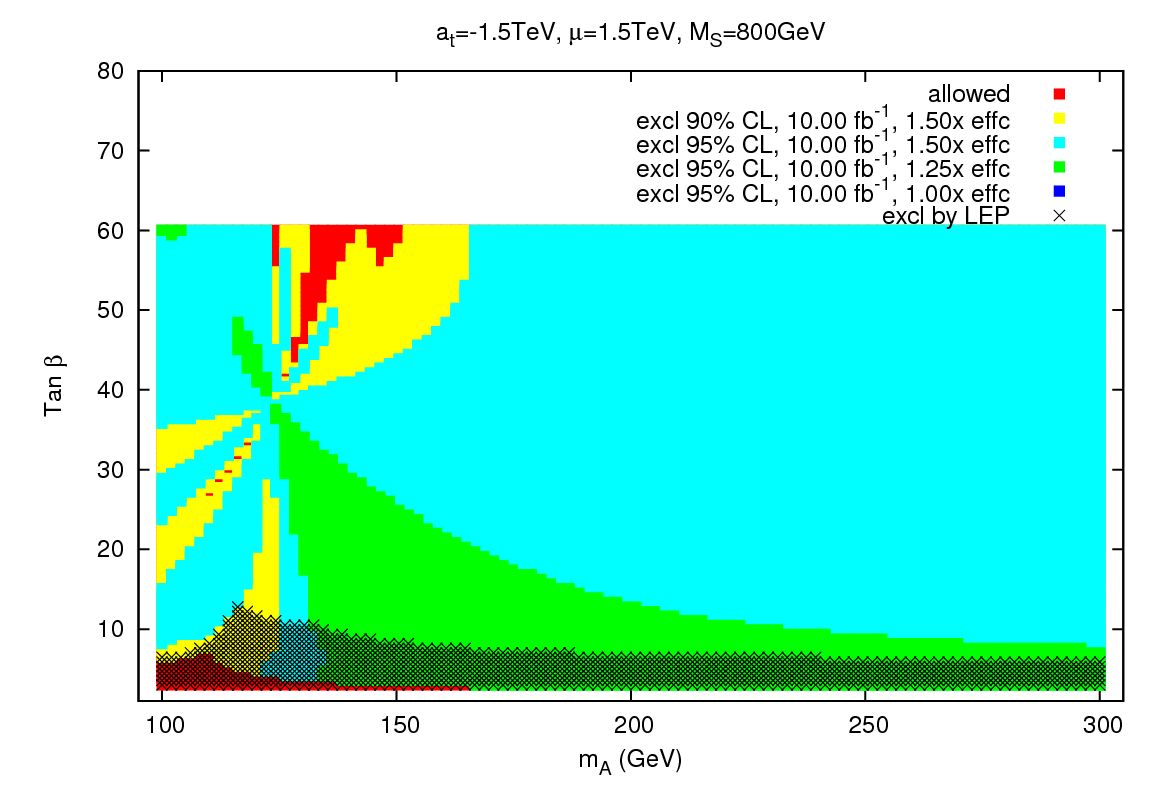
Also covered in our work is another benchmark scenario and the combination of the limits in each scenario with the h,H->ττ inclusive search for the nonstandard Higgs- for those just interested in the results, all the plots are available here. However, there are other channels that we did not include such as h,H->γγ, and as mentioned previously our baseline SM constraint was slightly conservative. Therefore, what we have found are upper bounds on the efficiency and luminosity improvements necessary to explore large regions of the MSSM Higgs parameter space. Achieving the studied improvements is not an unreasonable goal, and hopefully this work will provide added enthusiasm and motivation for extending the Tevatron's run, continuing to refine the analysis techniques, and making the most of its capabilities in its final years of collisions. We are currently investigating the Tevatron reach for the MSSM Higgs sector with explicit CP violation, and plan to present those results in the near future.