The CDF Collaboration at the Tevatron has produced yesterday a preprint of a publication, meant to be published by Physical Review Letters, where they describe the first observation of the hadronic decay of vector boson pairs: a pair of W bosons, or a W and a Z, or two Z bosons produced together.
A signal of diboson production has been seen before at the Tevatron, but only when both particles decay to leptons, providing a clean signature. The new analysis presents for the first time a signal in a final state with jets, emerging from the large QCD background in a dijet mass distribution.
The signal has a calculated significance in excess of 5.3 standard deviations. Both CDF and DZERO have been competing to arrive at this "observation level" for years, using more standard and yet apparently more promising techniques than the one which wins the house today. The signature used by the new result in fact does not exploit charged leptons to trigger and select the events, and just relies on the signal of a neutrino to tag the boson that decayed leptonically; moreover, no neural network or extended likelihood is used to boost the signal purity, and just good, old-fashioned cuts are applied to the data. A true revenge of the old technique over the fancy advanced methods.
CDF measures a combined cross section for WW,WZ, and ZZ decays of 18.0+-3.8 picobarns, in very good agreement with theoretical predictions, which assess the total cross section of those three processes at 16.8 picobarns.
Finding this signal was very important because it is a prerequisite for all low-mass Higgs boson searches at the Tevatron: the Higgs boson, if it has a mass lower than 135 GeV, decays predominantly into jet pairs, and can only be found if accompanied by a leptonically-decaying vector boson. The signature of associated WH/ZH production is thus exactly the same as the one unearthed in the new CDF analysis, and in fact, if the Higgs boson exists and has a mass in the 120 GeV ballpark, the published 45,000 event distribution by CDF should contain about 40 Higgs events (!), if the Standard Model is correct.
Let me stop here, because I was already crucified once when I speculated that a dijet mass distribution which contained a signal of Z boson decays to b-quark jet pairs could in principle also contain some signal of a supersymmetric Higgs boson, if another analysis which had sought for that SUSY particle were indeed seeing its first glimpse. That was in 2007, and a lot of water has passed under the bridges since then. Most of my colleagues seem to have understood, inside and outside the CDF collaboration, that this blog is an instrument of science popularization and not a demoniac means of making CDF a less authoritative or believable source. A few die-hard anti-bloggers still exist around, however: Mario M. P., Lina G., Beate H.... I do not want to instigate their crusading attitude today, so as I said, let me stop here.
The facts outlined above are by no means an exhaustive summary of what I am discussing below, but they should suffice for whomever cannot invest ten minutes of his or her life into understanding in more detail this important bit of particle physics. So let me start over now. First, a little bit of the physics of production and decay of these odd couples. If you are a particle physicist, you might consider skipping the next two paragraphs -or just the first, if you do not remember how a diboson pair is produced at a hadron collider.
W and Z bosons, the protagonists
The two protagonists of this physical process are the W and the Z boson. A quarter of a century after their discovery -by Carlo Rubbia (right) and his collaborators, with the UA1 detector at CERN- these amazing particles continue to take center stage in cutting-edge fundamental physics. The W boson is an elementary corpuscle whose mass is amazingly large if compared to that of the elementary building blocks of ordinary matter: it is point-like to the best of our knowledge, and yet it has a mass 160,000 times that of an electron; it in fact exceeds the combined mass of four water molecules... We could quench the thirst of Maxwell's daemon with four water molecules, while I guess it would complain if we fed it with a W boson.
But the W is not just massive: it is also a fundamental ingredient in the Zoo of particle physics. Without it stars would not burn, radioactivity would not exist, and Rubbia would be best known for his failed discovery of neutral currents. The W mediates the interaction called "weak force", and is thus responsible for the transmutation of quarks of different flavor into each other.
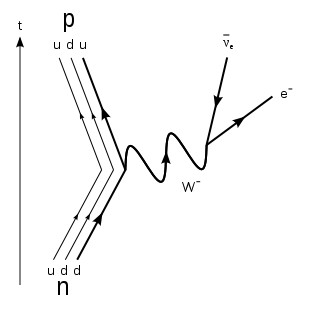The diagram of beta decay - the process whereby a neutron turns into a proton, which is at the basis of most radioactive decays - is shown in the graph on the right to put in good evidence the role of the W boson: one of the two down-type quarks in the neutron transmutes into a up-type quark, releasing one unit of electric charge together with another exotic attribute called hypercharge, in the form of a virtual W boson. The newly-bred up-quark remains tightly bound within the original hadron, which is now a proton; the W boson instead immediately disintegrates, yielding an electron and a anti-neutrino. Time in this graph is flowing from bottom to top as shown by the arrow on the left; each line represent the propagation of one elementary particle: on the left the three quarks making up a neutron and then a proton; on the right, the electron and neutrino originated from the charged weak current shown by the wiggly line at the center.The W boson in the diagram of beta decay above is virtual, since it has a mass way smaller than the nominal 80.4 GeV of real W particles. In general, however, I would argue that "virtual" is a misnomer. Any elementary particle with a finite lifetime has a mass that is only on average equal to what we call its "rest mass". The mass can be smaller or larger, and there is in fact a function called "Breit-Wigner", which describes how probable any mass is. Mind you: any mass! Even ones close to zero are possible, and a particle should not be deemed virtual if it is off its mass shell.
There are several things which interest us today in the prototypal process shown above. The first one is the W boson's versatility: it talks to both quarks (on the left, where it "couples" with the quark line) and leptons (on the right, where its decay highlights the boson's capability to attach itself to a leptonic line too). This means that weak interactions are felt universally by quarks and leptons alike; to us, it means that W bosons can be produced in hadronic collisions -where quark lines may emit them much like the down-type quark does in the graph above- and can decay into pairs of quarks as well as leptons.
The seminal nature of beta decay is not a surprise: by studying it, physicists in the 1930s started a long learning process which eventually led to the formulation of the Standard Model, over thirty years afterwards. However, to get there a much more elusive particle -W's neutral brother, the Z- had to be also figured out.
The Z boson is even slightly heavier than the W - it has a mass of 91.2 GeV, more or less the mass of the smallest droplet of salty water you could form, by stirring together two water molecules and one molecule of sodium chloride in an improbable glass. Yet like the W, the Z is exactly pointlike. And unlike the W, the Z does not even possess an electric charge, and it does not mediate quark or lepton transmutations, despite coupling to both those kinds of matter fields. What is its use ? It does not burn stars, it does not make radioactivity counters click.
Yet without the Z, the W could not exist, nor would the photon. The Z, together with the W^+ and the W^- and the photon, makes a quartet of states which are as loyal on one another in the Standard Model as are Athos, Porthos, and Aramis with D'Artagnan in the famous novel by Alexandre Dumas, "Les trois mousquetaires".
The Z boson has an illustrious story, too: it was only through its indirect observation in bubble chamber images such as the one on the left, showing the scattering of neutrinos off electrons (in this case) and nuclei, that physicists decided to fish out a paper which had rested for six long years on a dusty shelf, and elect it as THE theory of electroweak interactions, in 1973. Without predicting the existence of the Z and its neutral currents, the Standard Model of Glashow, Salam, and Weinberg would have remained an imaginative but failed attempt at explaining the organization of matter and forces at the subatomic level.Diboson production: an intriguing process
Now let us come to the process by which production of a pair of these bosons occurs. Why a pair, first of all, and not one at a time?
Sure, single W or Z production is not just possible, but it is actually a much more frequent process. The SppS collider at CERN in fact allowed these particles to be produced one at a time, and they were thus discovered by Rubbia in 1983-84. A few years later, the Large Electron-Positron (LEP) collider was built, and in its 91 GeV collisions millions of Z bosons, again produced one at a time, were collected and studied in exquisite detail.
Diboson production was then seen at the Tevatron proton-antiproton collider for the first time, and then studied by an upgraded LEP II, where the energy of the beams was made high enough to make pairs of W bosons together. Later still, WZ production was seen at the Tevatron, and finally, more recently, ZZ production has also been discovered.
The production of pairs of vector bosons is one very interesting process because it allows us to test how they couple to one another, something which one cannot do by producing one at a time (unless the production process arises through vector boson fusion, but that is a very rare reaction and I will not explain it here).
Basically, you can imagine a three-line graph describing three bosons joining at a space-time point. You can think of it as one boson decaying into two others, or two of them colliding and fusing into a third; it does not matter: all what matters is that the diagram does describe reactions which can and do occur in Nature (the bitch, not the magazine).
Since the intensity of the coupling of vector bosons to each other is a very direct probe of the Standard Model, and one where surprises might be lurking, studying the production of pairs of vector bosons has always been a top priority of particle physicists. Now, however, that we are looking for the Higgs boson, we have additional reasons to study the process.
For one thing, the Higgs may decay into WW or ZZ pairs, giving rise to the same final state as the one that is studied in diboson production. But in addition, the Higgs itself can be produced together with one vector boson, just as if it was part of the family itself.
The so-called "associated production" of a Higgs boson and a W or a Z boson is indeed the "golden" process to search for at the Tevatron, if one wants to find evidence for the Higgs. The reason is that the Higgs boson, which has been shown to be most likely not much heavier than the lower mass bound set on it by LEP II (114 GeV), must then decay into a pair of b-quarks, and not pairs of W bosons as it would if it were heavier.
By decaying to b-quark pairs it becomes utterly impossible for us to distinguish a Higgs boson from Quantum ChromoDynamics (QCD) backgrounds, which create the same signature at a rate a gazillion times larger. Backgrounds win, unless the Higgs is accompanied by a W or Z boson: associated production, that is. The leptonic decay of the W or the Z provides a means to distinguish those few Higgs production events from all QCD processes, and the search for associated production becomes the best chance that CDF and DZERO have to discover a light Higgs boson.
So, if a WH or a ZH pair decays as we have described above, the total event signature sees a lepton-neutrino pair plus two b-quark jets (in the WH case), or a pair of charged leptons plus two b-quark jets (in the ZH case). That signature is called "semileptonic" with a misnomer which is good enough for us here. The same signature is what has been observed for the first time by CDF from WW/WZ/ZZ pairs, in the analysis I am now going to describe.
The CDF analysis
The new CDF analysis of diboson production is innovative because of its old-fashioned nature.
The apparent oxymoron is soon clarified: in the last ten years we have seen the increasing use of analysis techniques based on advanced methods to classify events as likely signal or background ones. They have fancy names, like Neural networks, Boosted decision trees, Matrix-element probability weighting, Extended relative likelihoods, Random forests, Hyperballs, What-not.
The ones mentioned above are indeed quite powerful analysis methods, but they share a common soft spot: they rely on the simulation of signal and background processes much more than the simpler cut-based analysis techniques en vogue in the past did. Physicists nowadays have become confident in their Monte Carlo simulations, so those advanced techniques are now widespread. However, to establish a new signal, a good old-fashioned cut-based analysis might still be the best option.
The old-fashioned style, however, stops there. In order to find decays of vector boson pairs the authors of the analysis -Gene Flanagan (Purdue University), John Freeman (FNAL), Alexandre Pranko (FNAL), and Vadim Rusu (FNAL) decided to completely overturn the usual strategy by means of which leptonic decays of vector bosons are found -the prerequisite which is the necessary first step before one can go on to search a second, hadronic vector boson signal in the selected events. While for that first step one usually relied on datasets containing a well-identified, high-energy electron or muon, the CDF authors totally ignored these final state particles. Instead, they focused on a tight, straight cut on the amount of missing transverse energy present in the event.
Missing transverse energy is a quantity that one can reconstruct by measuring the imbalance, in the plane orthogonal to the beams, in the amount of energy detected in the calorimeter system -a cylindrical detector which measures the energy of both charged and neutral particles by having them hit nuclei of heavy elements and counting the debris. Since the incoming protons and antiprotons have no momentum in the plane orthogonal to the beam, whatever is produced in a collision must overall conserve the total momentum in the transverse plane: so the vector sum of particles momenta (or energies, if we approximate particle masses to zero) in this plane should be null. If it is not null, its magnitude is called "missing transverse energy". A significant amount of missing energy is a clue that some particles left the detector without depositing their energy in it.
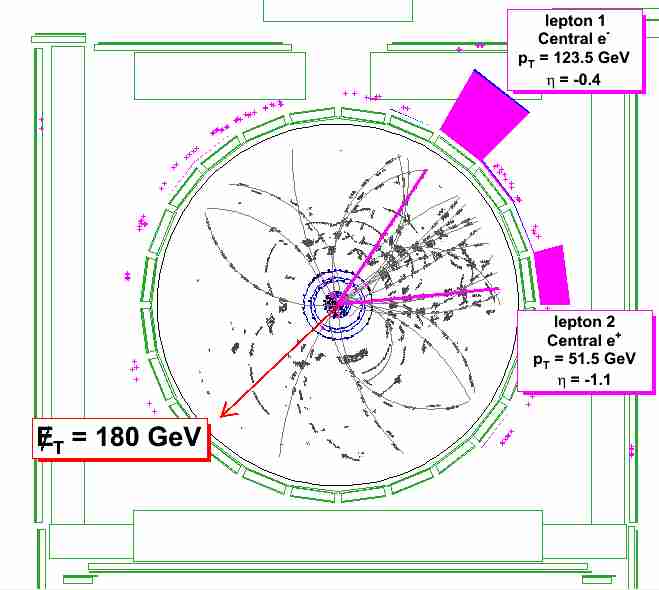In the event display shown on the right you can see the signature observed in CDF from a fully leptonic decay of a pair of Z bosons. One of the two decayed to an electron-positron pair, the purple tracks pointing toward the upper right, where calorimetric energy deposits are also shown in purple; the other produced two neutrinos which escaped the detector in the opposite direction, leaving behind some missing transverse energy pointing in the direction of the red arrow.When a significant amount of missing transverse energy is present, there are two hypotheses. The first is that the calorimeters measured badly some of the energy deposited there by particles produced in the collision; the second is that a neutrino carried away unseen the missing energy and momentum. Neutrinos do not interact in the detector, so whenever one is present, missing transverse energy is all one can see.
Missing energy is not nearly measured as precisely as electrons or muons momenta; also, its signal is much more easily mimicked by backgrounds. However, its use to find leptonic decays carries a significant advantage with respect to the standard identification of charged leptons, one which I am proud to say was recognized, demonstrated, and put to work for the first time by my student Giorgio Cortiana and I, in a measurement we made of the top quark pair production cross section which turned out to be the third most sensitive one by CDF in 2005.
What we realized back then, and what is used in the present analysis, is that because of its being a signal of something unseen, missing energy is a 100% efficient signature, while whenever you try to detect something, like a well-measured electron or muon, you are unavoidably subjected to small but nagging inefficiencies of the detector. Cuts are required to remove not-so-good electron or muon signals, and cuts reduce efficiency, and ultimately have a hit on the amount of signal one may find.
By selecting large missing transverse energy, the new CDF analysis -as our top mass cross section- is sensitive to many different topologies that the ordinary analysis involving charged leptons has to abandon on square one:
- W -> e nu decays when the electron did not hit a central, well-understood, "fiducial" region of the detector, or not sufficiently clean;
- W -> mu nu decays of the same kind;
- W -> tau nu decays altogether (tau leptons are very hard to distinguish from hadronic jets);
- Z -> nu nu decays altogether -these do not contain charged leptons;
- Z -> tau tau decays altogether, as explained above.
- some residual Z->ee, Z-> mu mu decays where both leptons failed the selection requirements -a very unlikely but still possible occurrence.
Of course, missing transverse energy requires several corrections before it can be used with success by itself for the task of selecting vector boson decays. But it is possible to do it, and the authors did it masterfully.
The simplicity of the analysis is its biggest atout, because once significant missing energy is established in an event, two jets are required. Events with missing Et and jets are selected, and the invariant mass of the two jets is studied, to search for a enhancement -a bump- in the spectrum, at the mass value where W and Z bosons should contribute.
We have seen above that W and Z masses differ by about 10 GeV; however, the mass resolution of the CDF detector is insufficient to distinguish the two signals. For that reason, a template is constructed which combines the contributions expected by W->jj and Z->jj decays from the expected mixture of WW, WZ, and ZZ events collected after the selection of large missing transverse energy. This template is used to fit the data together with a background template, which includes all other Standard Model processes which produce missing transverse energy together with two energetic jets.
Here we arrive at the most astonishing thing about the whole analysis: whomever thought that a simple missing Et selection would be unable to reduce significantly the background from Quantum ChromoDynamics -quark and gluon scatterings, yielding jets in the detector, and sometimes badly measured ones which result in fake missing Et- is up for a surprise. After the selection of missing Et above 60 GeV, backgroudns are constituted for the largest part by real W and Z bosons, yielding neutrinos, accompanied by jets due to QCD radiation; the dreaded purely hadronic component is reduced to a marginal role!
To demonstrate that QCD is marginalized, let us give a look at the plot below, which shows a variable which well discriminates the electroweak from the QCD background: it is the azimuthal angle between the direction of the energy imbalance and the direction of the closest hadronic jet. In hadronic events, where the missing Et is due to a fluctuation in the calorimetric measurement, this angle is typically small: it is a jet which was badly measured what causes the missing Et, so the two are usually aligned. In W+jets or Z+jets production processes, instead, the angle has a flat distribution.
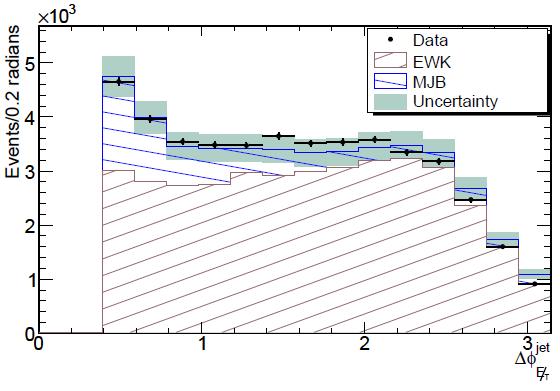
The QCD component (labeled "MJB" for "multijet background) is clearly visible in the plot as a enhancement at small angles, as predicted by the background model. Note how the data -shown by black points with error bars- obeys the shape resulting from the sum of a large electroweak and a small QCD component, validating the background model.
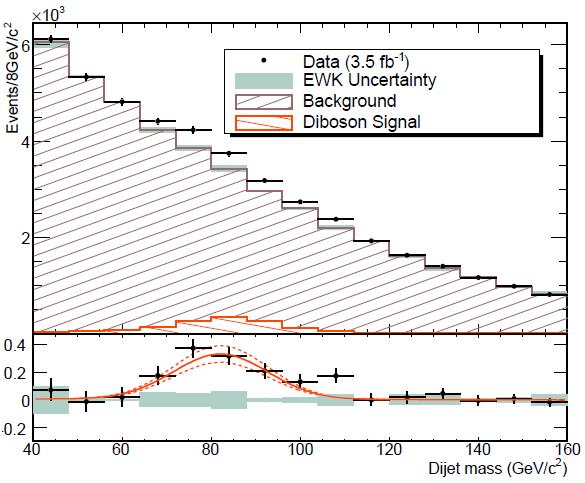
A fit to the dijet mass distribution shown above extracts a significant fraction of signal events, as shown in the bottom part of the plot, where the excess from signal events is shown after a background subtraction. The signal behaves as predicted by the Monte Carlo model, but it is remarkable that one can see it by eye already in the top plot, where in the region between 70 and 100 GeV the experimental data points make some kind of a "shoulder", a hint of the enhancement due to the diboson signal. The fit evaluates the enhancement as a 1516 events component, which is easily translated in a cross-section for the combined production of WW, WZ, and ZZ boson pairs. The computed cross section is in excellent agreement with the theoretical prediction, and this is a nice confirmation that the results are on solid ground.
A note on the significance of the extracted signal
If you have read this column carefully enough during the last month, you have probably already figured out that I care for exact evaluations of the significance of marginal particle signals. In this case, I can tell you that the signal is indeed exceeding the 5-sigma significance level, head and shoulders. You can trust me this time not only because of my reputation and my record -after all, it is easy to recognize that whomever has a reputation usually uses it in a way that endangers it. You can trust me this time because I have been the chair of the internal review committee of this result. Our committee, which included Monica D'onofrio and Fabrizio Margaroli, both experienced collaborators, steered this result to publication only after a careful dissection of the technique and all the nuisances that divide a perfect result from a sloppy one. So I can tell you something more about the significance than what you find in the paper, although of course I am not authorized to distribute material not approved for public consumption.
Indeed, the significance estimate is one of the most important things about the whole analysis, because on it is based the claim made in the title, that the result constitutes a "first observation" of hadronic diboson decays. A simple way to evaluate it is to make the dumb "signal divided by error" calculation: that is, if we measure a signal of 1516 events and attribute an error of 239 events to that number, the determination differs from zero by 1516/239=6.34 standard deviations.
The CDF result however includes a systematic uncertainty: it is actually quoted as 1516+-239+-144 events in the paper, where the latter number is an evaluation of the effect on the fitted signal that may come from systematical effects not included in the statistical extraction. A simple-minded approach to combine the two uncertainties is to add them "in quadrature": this assumes two things. The first is that the sources of uncertainty are independent, and it is usually the case; the second is that the systematic uncertainties have a Gaussian behavior -that is, that it is only 3% probable that a deviation of twice 144 events is due to those systematic sources, or only 0.2% probable that a three-sigma fluctuation occurs: a Gaussian distribution of the associated fluctuation, that is.
If we do that simple-minded accounting, we find that 1516 differs from zero by 1516/sqrt(239^2+144^4)= 5.4 standard deviations. But this is not the right way to do it, of course. Prompted by the reviewers, the analysis authors instead studied more carefully the five main sources of systematic error in the measured signal rate, and found that only one of them had the potential to affect the measurement appreciably, while all others were completely irrelevant. A dedicated study was then carried out to examine that source of uncertainty in great detail, and a more precise estimate of the signal significance was finally obtained using standard statistical methods by studying that variation.
The final number obtained, 5.3 standard deviations, shows that the single strongest systematical uncertainty has a stronger effect than all the systematics taken together when an incorrect Gaussian approximation is used. The Devil, indeed, is in the details; but this time, not even a black Devil could change the result from an "observation-level" one to a simple "evidence" of the sought process.
In conclusion...
In a comment you can find in the thread of the blog post where I first announced this new result yesterday, Lubos Motl claims I was not clear enough in explaining how this result can be of any use for Higgs searches. Of course: my post was just an announcement, and this article is the proof that I meant business when I said that a deeper explanation would come. So let me elaborate on the point raised by Lubos here. Apart from what has been said above about the similarity of the WH/ZH production process with the WW/WZ/ZZ production, and the note about the fact that a light Higgs boson almost always decays to jet pairs, there is another point to make here.
Indeed, the analysis which proves most sensitive to the diboson signal turns out to be one which neglects charged leptons, and does a very straightforward selection just based on missing transverse energy. I then wonder what will happen by selecting, among the 45,000 events appearing in the mass distribution you have seen above, events where one of the jets contains hints of the decay of a b-quark.
Of course we are still far from being able to see a Higgs boson in that distribution, but I would be extremely pleased if we saw a hint of WZ/ZZ production with one Z decaying to a pair of b-quark jets. That is possible because the W decay to jet pairs only produces light-quark jets, and almost never b-quarks: by selecting b-jets, one is only left with the Z->bb signal accompanying a leptonic W or Z decay.
Seeing that signal in the dijet mass distribution would really be one further long step in the right direction: and, given the moral suasion powers that being the chair of the analysis grant me, I am in fact already bugging the authors to try that modification of the analysis on their 45,000 event sample... My guess is that b-tagging one jet would reduce the 1500 event signal to about 150, while among the 45,000 background dijet pairs only about one or two thousand would remain. 150 events in 2000: a Z signal should be observable there! And if you know me and my past research, you know how affectionate I am to the Z->bb decay: it fruited me a Ph.D. thesis and I have worked on it for several years in the past. So I have a lot to look forward to in this analysis: a Z signal, and one day, maybe even a smaller bump at 120-130 GeV...
Comments