A couple of months ago I wrote here about the first observation of a process called "diboson production", a quite rare occurrence in hadronic collisions: for the first time, the CDF collaboration could observe that rare process in events containing hadronic jets, which are usually riddled by enormous backgrounds.

The significance of that result, which added no real information to our knowledge of subnuclear physics, was stressed in my article to be the demonstration that similar kinds of events can indeed be mined for rare signals despite the large backgrounds. One of these rare signals which I did mention was of course the production of Higgs bosons, which may in fact yield the very same signature as the one put in evidence in that study.

Today I wish to report on two parallel searches for the same kind of events by members of the same collaboration. The first one has been performed by three young and skilled Italian colleagues (A.Annovi, P.Catastini, and V.Cavaliere), the second one by a larger group of quite experienced physicists from the US, Spain, and Canada. These two groups used different techniques from the one already discussed here.

The two new results deserve as much praise as the former one, except that they are obtained with the more standard approach of explicitly looking for charged leptons, which guarantee an efficient trigger and a powerful background reduction.

Since I lack the stimulus to challenge myself into writing a better ouverture on vector boson physics than the one I produced two months ago I will admit defeat, and rather than introducing the topic as carefully as I did back then, I will offer below only a quick note on the different decay modes of dibosons, and then jump to a description of the new analyses. Those of you who would like to know more about the physics of vector boson production and their pair-production in hadron collisions are kindly suggested to read the other post first.

Diboson production in the mixed "lepton plus jet" final state

In proton-antiproton collisions the associated production of two W bosons, or a W boson and a Z boson, is a rare occurrence: once per five billion collisions. These processes have been observed at the Tevatron a few years ago by relying on the decay to charged electrons or muons of both the bosons, because in that case, although the signal is tiny, backgrounds are almost non-existent. Only W and Z decays produce clean, isolated, high-momentum electrons or muons, and a fully leptonic WW or WZ decay produces at least two of them.

Allowing one of the two bosons to decay to quark pairs (or ), when each quark yields an energetic hadronic jet, increases the number of good decays significantly, since there are three kinds of quarks per every lepton (remember, quarks have colour charge, and although we do not "see" it, this affects the number of different quarks that claim their share of W or Z decays), but it also increases the background so dramatically that the mixed "lepton plus jet" signature has only been conclusively observed this year. The background is due to the production of events containing just one W or Z (decaying into leptons) while the two hadronic jets come from quantum chromodynamics (QCD) radiation of gluons off the initial quarks that give rise to the boson.

And in case you were wondering: the "all-jet" decay, involving decays to quark pairs of both bosons, is essentially unobservable at a hadron collider, because the WW/WZ signal cannot -just cannot- be distinguished from 4-jet events due to purely quantum-chromodynamical processes.

In a nutshell, the experimental signature of mixed decay of dibosons used by CDF in the new searches consists in a high-energy electron or muon accompanied by significant missing transverse energy, plus two hadronic jets. The lepton and the missing energy arise from one leptonic W decay, while the two jets arise from the hadronic decay of the other W (for WW production) or the Z (in case of a WZ event).

The first analysis: a simple shape fit of the mass distribution

The first analysis I summarize here is the one by the team of young Italian physicists, which is based on a dataset corresponding to 3.9 inverse femtobarns of proton-antiproton collisions collected by the CDF detector during Run II. After a selection of events with a clean W \to l nu signature and two jets, the various Standard Model processes thought to contribute are studied to carefully determine the invariant mass distribution of the jet pairs which is expected in each of them. The dijet mass is in fact the single most discriminating observable quantity between diboson production and all other backgrounds.

There are four different Standard Model processes which contribute appreciably to the selected data sample. The production of one W boson with two jets from QCD radiation dominates, but it is not the only one. The equivalent process with a Z in place of the W can produce the signal signature when one of the two leptons from Z decay fails to be reconstructed by the detector: in that case, the transverse component of the energy it carried away gets accounted as "missing transverse energy", and comes to constitute a neutrino signature. A third process to consider is top quark pair production: top quarks decay into a W boson and a b-quark jet, and a "lepton plus jets" final state is easy to obtain from a decay if a few hadronic jets fail to pass the reconstruction criteria or be detected. Finally, QCD jets can sometimes produce a fake electron or muon signature, and missing transverse energy may arise from a wrong measurement of the energy in the calorimeter; this is a rare combined occurrence, but QCD produces jet events with such a large rate that the final dataset does contain a sizable number of such events.

The table on the right shows the expected rate of events from the various sources, separately for events where the W signature is provided by a high-energy electron and for events where the task is fulfilled by a high-momentum muon. As you can see, the diboson signal is expected to amount to about 3% of the sample. The rate of the various processes is estimated by a combination of methods exploiting both Monte Carlo simulations and the data themselves. The total number of events (second-to-last line) is in good agreement with observed counts (last line).

The real number of dibosons contained in the data is extracted from a fit to the dijet mass distribution. Below you can see the mass spectrum of the data, compared with the sum of backgrounds and signal. A bump is evident around 80-90 GeV, where W and Z decays to jet pairs in the signal events contribute. All backgrounds have a smooth mass distribution, and the fit can discriminate the electroweak processes (W and Z plus jets, and top pairs, collectively shown in green) and QCD (in blue).



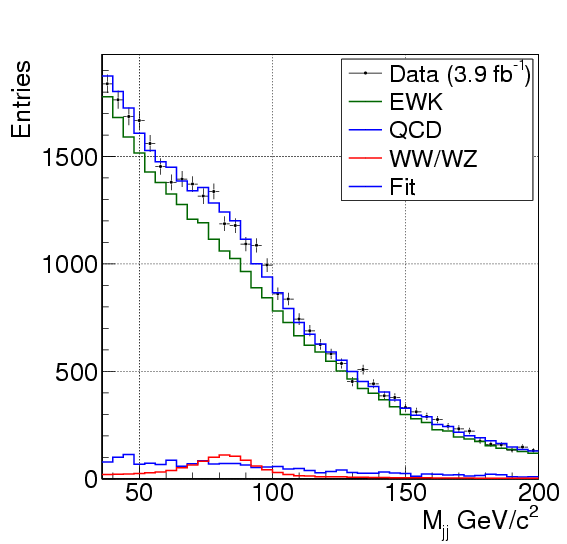
From the number of events extracted by the fit, the combined cross section for WW and WZ production is measured at 14.4+-3.1 +-2.2 pb, in good agreement with Standard Model predictions. The fitted signal has a statistical significance of 4.6 standard deviations: smaller than the large signal extracted with the inclusive missing transverse energy search I described two months ago, but still compelling evidence for the diboson signal. If you cannot resist comparing the two analyses, you will maybe end up noticing that the present one produces a similarly prominent mass peak (check the mass distribution of the missing Et-based analysis on the right), but the need of reconstructing a good charged lepton reduces the statistics significantly. Moreover, the inclusive search using missing transverse energy accepts more events because it is sensitive to ZZ production too, as well as to tau-lepton decays of the bosons. All in all, this new result focuses on a better-understood, smaller sample of signal events, and it is just nice to see CDF pull it off.


The second analysis: a matrix-element method

The other result on diboson production in the "lepton plus jets" final state uses a so-called "matrix element technique" to enrich the data of signal events. This means considering for each event the measured characteristics of the charged lepton, the missing energy, and the two jets, and determining the probability that these may have arisen from the signal or from different background processes. The probability that a given final state has arisen from one process or another is evaluated by working backwards from measured quantities to the different production diagrams (you know, the Feynman graphs) of the various possible processes. To reverse-engineer from the measured quantities to the four-body kinematics that characterizes one particular configuration, one needs "transfer functions" which describe, e.g., how a produced quark might have ended up being measured by the detector.

Hmmm, not altogether too clear, is it ? Let me make a simplified example involving only jet energies and the discrimination of WW signal from background. Imagine your event contains two jets with observed energies of 60 and 40 GeV: we know that they may be the result of the hadronization of quarks with almost any energy, but the likely quark energies roughly peak at 60 and 40 GeV, respectively. The transfer function of a quark to a jet is the probability that a quark of energy  has resulted in a measured energy . If you now know, from a calculation of the matrix element of the WW process and the matrix element of the  process, the functional form of the probabilities to observe the energy of the two quarks, say and , you can integrate:

,
.

In summary, you are asking the question: if I saw these two jet energies, how likely is that I have a WW event in my hands ? How likely it is that it is a ttbar event instead ? The smartest discriminant quantity you can construct to decide if you have a signal event is the ratio of the probabilities, say . This is a simplified example of what is called "Event probability discriminant" (EPD) in the analysis.

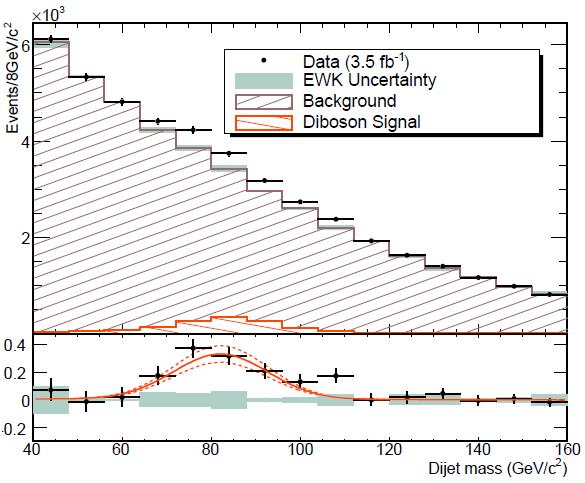
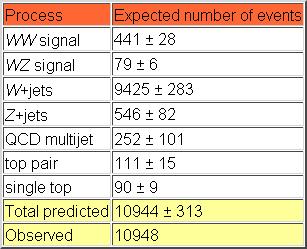Of course, the real method is quite a bit more complicated, but we have no business delving in those details. The matrix element analysis applies a much tighter selection than the one of the Italian team, and uses a smaller amount of data (2.7 inverse femtobarns). Because of that, the number of events from the various processes contributing to the dataset is smaller, as shown in the table on the right.

The EPD discriminant is finally fit as the sum of the various contributing processes. You can see the results in the plot below: the signal is shown as the red histogram in the stack. The horizontal axis describes the value of EPD, the data are shown as points with error bars, and the sum of all processes neatly reproduces the observed distribution. In the inset you can see that the dijet mass distribution for high-EPD-value events does contain "red" events which peak at the right mass. However, the background events also peak there, because the EPD is quite sensitive to the dijet mass, which is, as I noted above already, by far the most powerful discriminant of this kind of diboson decays.



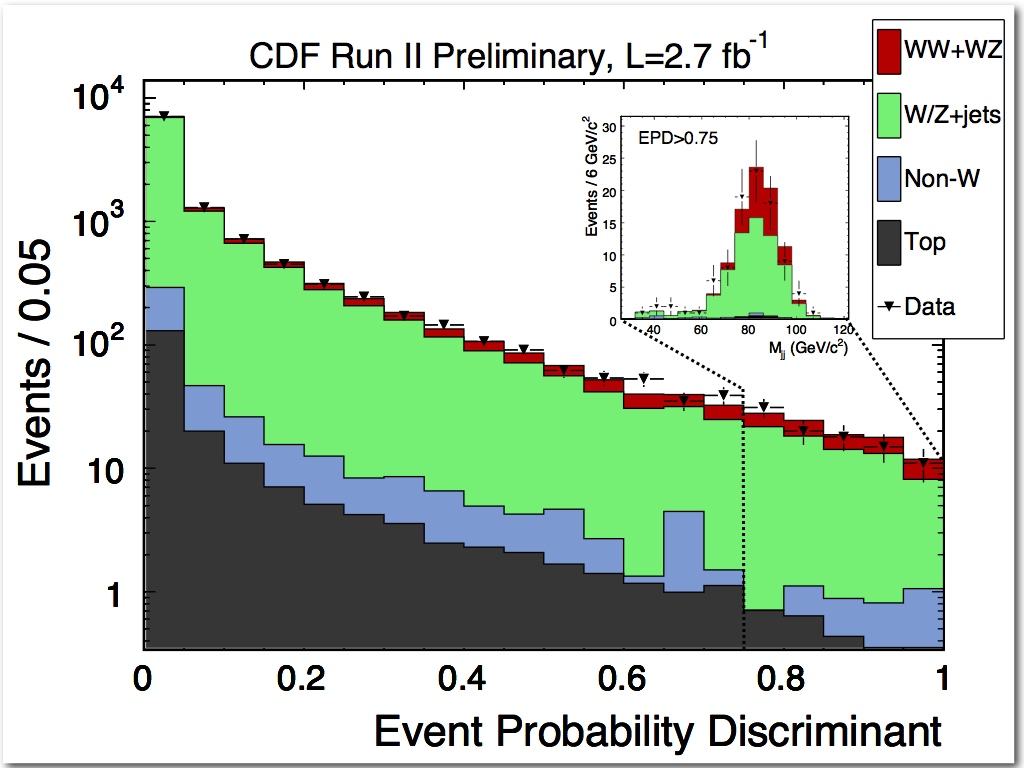
From the measured fraction of signal events determined by the fit to the EPD distribution, the combined cross section of WW and WZ is measured this time at 17.7+-3.9 picobarns: a larger value than the one found by the other analysis, but still in good agreement with Standard Model predictions. Finally, the significance of the signal is assessed at way above observation level: 5.4 standard deviations.

What remains to do here is to congratulate with my CDF colleagues for providing, in the matter of a few months, not just one, but three different measurements of the diboson cross section using jet decays. And since each of them has a different slant and a slightly different flavour, each provides valuable information. One example ? While the two analyses described today are based largely on the same data, and overlap significantly in their final candidate samples, the fact that they both succeed in independent ways, and provide compatible results, validates both methods. The EPD discriminant is one of those high-level variables that have been recently frowned upon by envious skeptics of the Tevatron results on Higgs boson physics. The combination of these two analyses shows that the EPD method is slightly more powerful, but essentially just as valid, as an old-fashioned fitting of the most powerful distribution.