But what the heck is a global fit ?
A "fit" is a mathematical procedure based on the concept of finding the value of some parameters which best agrees with the input data, given some assumed mathematical relationship between data and parameters; the adjective "global" just means that one is throwing at the fit all the information available, in order to have the most accurate estimate of the parameters.
An example will clarify matters for those of you who never had the pleasure to fiddle with minimization algorithms and similar trivialities. Suppose you want to know how fast your kid grows, in inches per year. You have four data points: measurements you took three years ago (40 inches), two years ago (43 inches), one year ago (46.5 inches), and yesterday (49.5 inches).
A "know-nothing" approach would lead you to take the two external measurements, 49.5" and 40", and divide by three, obtaining an estimate growth per year of 3.17 inches. But you can obtain a slightly more precise estimate if you work under the assumption that the growth per year is constant.
You can then find, by means of a mathematical procedure called "least-squares fit", the linear relationship which best agrees with the observed data; not just the two extreme points, but also the two inner ones, which you discarded in your quick-and-dirty averaging. The resulting "slope" of the linear relationship between year and height will again be the wanted growth per year in inches; it will not be too different from the former one, but it will be one which makes the best use of the available information, given the assumed linear relationship between the data points.
Note that the use of a fit makes it explicit that you have a "model" to interpret your data: a linear relationship between your boy's height and age, in this case. The "know-nothing" approach also assumes a linear growth, but in that case users might forget they are using that assumption when they divide the height difference by a time interval. An assumption of some kind, however, is needed in any case! Without it, your question "how much does my kid grow per year" is not even a meaningful one.
The Standard Model
Anyway, back to subnuclear physics. What is our model in that case ? We call it the Standard Model, and we sometimes capitalize it to make it absolutely clear that we respect it highly. The Standard Model is the theory of fundamental interactions and it is an exceptionally successful theory, besides being elegant and remarkably simple. As simple as these things go, of course: you still need to study maths and physics for a decade or so before you understand its intricacies; but if seen from a distance, without getting one's hands dirty with complicated calculations, it is entirely appropriate to talk of a simple, eye-pleasing mathematical construction.
The reason of the success of the Standard Model is that in the course of the last forty years we have not yet found any physical process that departs from the phenomenology predicted by the theory: everything we have measured -and I am talking about thousands of different measurements of particle properties and reactions- conforms to the predictions of the theory.
Since the early seventies the Standard Model has been used to compute the production rate of particles at colliders, as well as the frequency of their different decays, the angular distributions of their decay products, etcetera. In order for these calculations to work, however, one needs to provide as input the experimentally measured value of a small but significant set of free parameters. These are fundamental quantities that the Model itself does not predict: some two dozens quark and lepton masses, plus the parameters of the mixing matrices, plus the mass of the Higgs boson.
But is it so, really ? Well, not exactly. The complex dynamics of fundamental particles allows the a-priori indetermined value of particle masses and other characteristics to be connected to each other. These dependencies do not exist if one considers the simplest particle reactions, and only arise because of "radiative corrections" - variations in the value of observable quantities due to quantum processes involving the loop of virtual particles.
It would take me the better part of this afternoon to make sense of radiative corrections at an elementary level (and this does not give for granted that this is at all possible). Radiative corrections are quantum effects that we can calculate with the Standard Model, and that "connect" to each other some of the free parameters. Among them, most notably, are the masses of the top quark, the W boson, and the Higgs boson; plus others, of course.
Global Fits at work: the case of the top quark
Fitting together all the experimentally measured properties of fundamental particles with the predictions of the Standard Model, which must be computed including the effects of these radiative corrections, is not exactly a simple task. However, it has been routinely done in the course of the last twenty years - that is, ever since the precise measurements coming from the LEP and SLC accelerators made this a worthwhile occupation.
So, for instance, back in the early nineties some of these die-hard fitters claimed that they had "predicted" the value of the top quark mass, based on the observed features of Z boson decay at LEP. This is actually not quite true - when the top quark mass was first measured, by the CDF experiment in April 1994, global fits to electroweak observables produced by different groups of theorists spanned a wide range of values, all however very carefully landing only in the allowed range of top masses, i.e. ones not yet excluded by experimental searches. See the graph below, which I compiled in 2002 for a talk at a conference (and then updated in 2004 with new measurements):
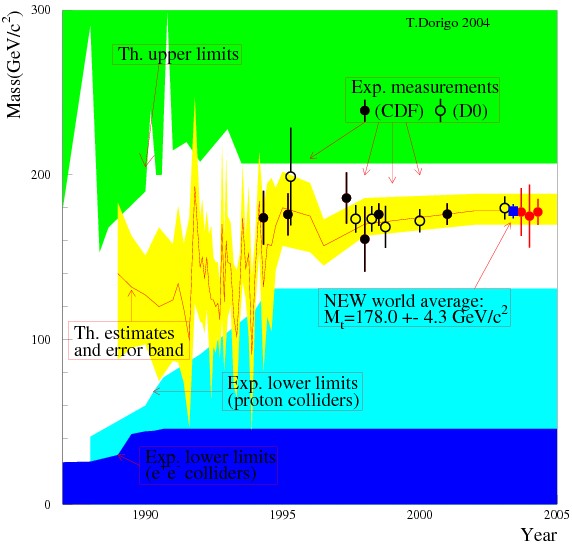
As you can see, the graph is quite busy. Let me help you decypher it. First of all, on the horizontal axis you find the years from 1987 to 2005, and on the vertical axis is the mass of the top quark. Second, the points with vertical error bars describe all the CDF and DZERO measurements of the top quark - the leftmost one is the one I cited above, 174 GeV, the first (and incredibly spot-on) measurement by CDF. Then there are blue and green "exclusion" regions: values of the top quark mass in these areas were excluded by direct or indirect searches (the top green area is coming from indirect theoretical speculations, the bottom blue ones come from direct collider searches).
Finally, the yellow band indicates different theoretical "estimates" of the top quark mass, coming from electroweak global fits to Standard Model observables. The red line shows the central value of these predictions, and moves around quite a bit, spanning a wide mass range while remaining mostly within the non-excluded mass range, until, after 1994, it quickly stabilizes at the measured value.
Don't get me wrong: indeed, indirect information from the global fits could predict the top quark mass with reasonable accuracy even before its discovery; but of course, nothing could substitute for a direct observation and measurement.
Global Fits and the Higgs - and beyond
And now, the same goes for the Higgs boson, with a difference however. The dependence of the Higgs boson mass on other observable quantities of the Standard Model is weaker than that of the top quark, so despite the precision of measurements of electroweak observables obtained at LEP II and the Tevatron, until last year we had still little clues on the true mass of the Higgs boson; we knew it had to be light -indeed global fits indicated a preferred mass in a mass range (M<114 GeV) already excluded by direct searches of the LEP II experiments), but anything between 114 GeV and 200 or so could do.
Now we have the Higgs too, and a pretty good measurement of its own mass too: ATLAS and CMS measurements can be combined to obtain a uncertainty of 0.4 GeV on the Higgs boson mass. This input allows global fits to be "overconstrained", in the sense that we can release in turn each one of the free parameters (whose value comes from direct measurements) and enjoy the power of radiative corrections, which give us a preferred value of that parameter in output, the value most consistent with all other inputs.
For some of the parameters which are less tightly correlated with others this game does not allow us to learn much; but if we run it on e.g. the W boson mass we are in for a surprise: despite the great precision with which the W boson mass has been measured (by CDF and DZERO, and also by the LEP II experiments), the global Standard Model fits produce a "measurement" (indirect, but still a measurement!) which is even more precise! See the graph below.
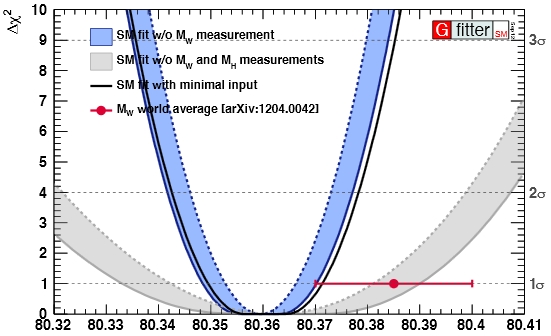
As you can see, the "width" of the blue parabola at the point of delta χ^2=1 is narrower than the experimental world average, symbolized by the horizontal error bar. (The wider parabola is the one which does not include the Higgs mass in the fit, highlighting how much information that latter input provides).
One example of a parameter for which direct determinations still win hands down is instead the top quark: as shown below in a graph similar to the one above, the experimental measurements have still a much smaller uncertainty than what can be obtained by global fits.
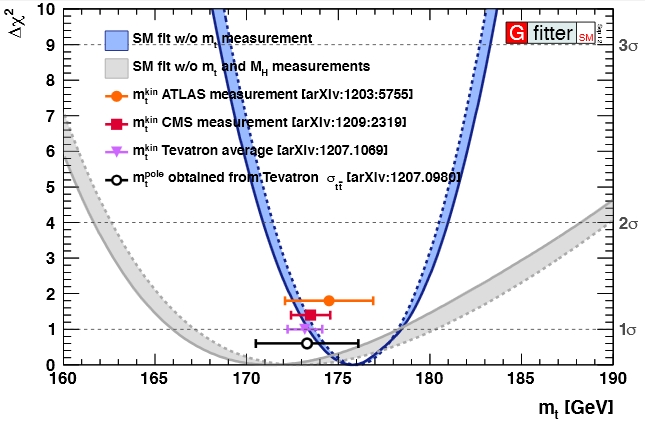
The figures above are courtesy gFitter - which does not just mean "global fitter", but is the symbol of the gfitter group.



Comments