As a member of two large scientific collaborations (CDF and CMS), I enjoy the benefit of seeing lots of scientific publications that carry my name as an author being produced at weekly rates. This is however also a burden, since I at the very least must try to ensure that I like the way the results are produced. I.e., that I agree with the details of how these scientific measurements are made.
Yes, we are talking about statistics. All the results of collider physics experiments require a certain amount of manipulation before they are offered to the consumer (say a theorist who wants to compare said result with his or her theory). And things can easily go wrong, because of the subtleties involved, compounded with the fact that physicists usually have the attitude that they can "reinvent the wheel" every time they need to. What I mean is that despite the existence of a huge statistics literature on the correct procedures for combining measurements, obtaining confidence intervals, accounting for systematic uncertainties, and the like, often we ignore everything and put together methods of our own cooking.
So I sometimes need to complain with objectionable statistics procedures used by my colleagues. If I look elsewhere, though, the significance of the misdemeanour I may spot in the papers I co-author suddenly gets reduced. Not anything to rejoice about, but still, a conforting thought about one's standards.
Take this paper, published in the arxiv a few days ago. It is a measurement produced by the MINOS collaboration of neutrino and antineutrino fluxes.
Using the antineutrino interactions they recorded, MINOS tried to gauge whether those particles have oscillation frequencies which depend on the antineutrino direction of motion with respect to a reference frame centered on the Sun. The theory at the basis of this is an extension of the Standard Model whereby Lorentz invariance is violated: one of the effects one might think of would in fact be a sensitivity of the oscillation frequency on the direction of particle propagation.
The way MINOS derives upper limits on the parameters describing this possible effect is a rather complicated frequentist calculation. I could not really understand the details, maybe because I had little time to ponder over them. What attracted my attention was instead the non-chalant way (to be euphemistic) by means of which MINOS "combines" their antineutrino-derived 99.7% CL upper limits on the coefficients of this new physics model with previous ones derived from neutrino interactions.
[In order to be sure you understand what I am talking about, let me make a premise. A 99.7% confidence-level upper limit is the value of a parameter (in this case, the coefficient of this new physics model) above which there is a less than 0.3% chance of having obtained data as "extreme" as the ones at hand, given the unknown parameter value. Note that it is a random variable based on the observed data and the a-priori hypothesis on the probability density function of the data as a function of the unknown parameter.]
Now, for each studied parameter MINOS takes their 99.7% CL upper limit x1 on the parameter derived with antineutrino interactions, and combines it with earlier upper limit x2 derived with neutrino interactions with the following formula: 1/x^2 = 1/x1^2 + 1/x2^2. They so get new, tighter, upper limits x.
I find this, er - let me choose suitable words... Problematic. I will not go in the details nor deal with the implicit assumptions (Gaussians, no correlations between the systematics, etcetera), but please consider.
The "method" ignores the fact that confidence intervals are members of a thing called a confidence set. By themselves, any confidence interval taken by itself does not "cover" with the stated CL: for sure, it does not guarantee that "the probability that the true value of the parameter is within the bounds is 99.7%". Besides being wrong and a misinterpretation of the meaning of the confidence interva, that would be a statement a frequentist cannot make, since it involves associating a probability with a (unknown, but fixed) parameter value.
Rather, intervals "cover" in the sense of being members of a set which has that property. If I take two confidence intervals which are members of a 99.7% confidence set and combine them by adding the upper limits as in the formula above, I have no guarantee that the resulting x will "cover" as well with the same CL. In fact, it does not, in general. MINOS should instead take their central values, combine them with a maximum likelihood technique, and perform a Neyman construction or a similar limit-setting procedure based the resulting estimate. Sure, it takes a bit longer than doing the sum of the inverse squares of the upper limits. But it gets the correct value.
To show how wrong one can be with the formula used by MINOS, take the Gaussian measurement of a parameter. Take σ=1 for the Gaussian: this means, for instance, that if the unknown parameter is μ=3, there is then a 68% chance that your measurement x will be in the 2<x<4 interval. Since, however, what you know is your measurement and you want to draw conclusions on the unknown μ, you need to "invert the hypothesis". Let's say you measure x=2 and you want to know what is the maximum value possible for μ, at 95% confidence level. This requires producing a "Neyman construction" of the confidence interval. You will find that your limit is μ<3.64, as the union of all regions marked in blue in the graph below.
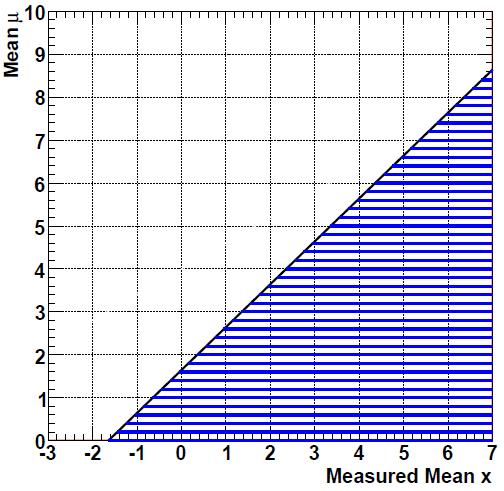
[In the graph, the highlighted region is constructed by asking, for each unknown value of μ on the y axis, what are the values of x which would not make the user suppose that μ is smaller, at the stated confidence level. This amounts to finding the point at which the integral of a unit Gaussian of mean μ has a value equal to 1-CL. For instance, for μ=3.4, the value x=2 is included; but for μ=3.8, it isn't. Upon obtaining a real measurement x*, one draws a vertical line and finds the upper value of mu which is contained in the highlighted region. That is the upper limit on the unknown parameter. Figure taken from R.Cousins, Arxiv:1109.2023 ]
And what if you got twice the measurement x=2, in independent measurements ? Could you then combine the limits as MINOS does ?
If you combine two x=2 measurements, each yielding μ_up<3.64 at 95%CL, according to the MINOS preprint you might do μ_comb=1/sqrt(1/μ1_up^2 + 1/μ2_up^2) = 2.57. Nice: you seem to have made great progress in your inference about the unknown μ. But unfortunately, the correct procedure is to first combine the measurement in a single pdf for the mean: this is x_ave=2, with a sigma of 1/sqrt(2). The limit at 95% CL is then μ<3.16, so quite a bit looser!
Also note that we are being cavalier here: if x1 and x2 become different, the inference one can draw worsens considerably in the correct case, while in the MINOS method at most reduces to the most stringent of the two limits. For instance, x1=2, x2=4 yields the combined limit μ<4.16, while MINOS would get μ<3.06. This is consistent with the mistake of ignoring that the two confidence limits belong to the same confidence set...
I sincerely hope MINOS will not submit the paper as is to a journal...





Comments