This result, which is probably going to be the definitive one by the Tevatron experiments, reaches a precision in the top mass which is comparable to the precision of the scale you have in your bathroom, despite the fact that measuring your body weight is a quite simpler matter than determining the mass of an elementary particle, let alone one which exists for less than a trillionth of a trillionth of a second.
A digression
I bet you are unfamiliar with trillionths. A trillionth of your life span is little more than a millisecond, so imagine how quickly does a top quark decays! In order to make room for the second "trillionth" we need to compare to something still unfamiliar to us - the age of the universe. Still, a trillionth of a trillionth of the age of the universe is a quarter of a microsecond... We are led to the following statement:
"The top quark lifetime is to a second what a quarter of a microsecond is to the age of the universe."
I don't know about you, but it does not ring a bell. It appears that we are indeed powerless to appreciate how short is the lifetime of a top quark.
At this point you might interject that I should be talking about a mass measurement rather than about the lifetime of the particle, and since these are two quite different things, why am I insisting on the lifetime ? Indeed, no reason, other than explaining that in principle the short lifetime of a particle affects the precision of our measurement, given a finite sample of data in our hands.
To understand that, imagine that the scale in your bathroom is an old-fashioned one, featuring a hand pointing to a graduated arc. As you jump on the scale, the hand reaches the correct weight, but before stopping it oscillates back and forth a little, say for a few seconds. The oscillation may reflect the natural oscillation frequency of the springs which bear your weight, or may be a combination of that with the rest of the mechanics of the apparatus.
Anyway, now imagine you step on the scale and jump off in half a second; while you are on the scale, somebody takes a snapshot of the hand of the scale. Would the picture allow you to read off your precise weight ? No, because the oscillation did not have time to settle during the small time you were on the scale: the picture may show a reading which is significantly off your real weight.
With elementary particles, a similar thing happens: their fast decay prevents them to settle to a state of mass equal to the true "natural" mass they would have if they lived forever, so if one relied on a single measurement one would have to fight not just with the experimental resolution of the measuring device, but also with this intrinsic indetermination, which ultimately is due to Heisenberg's Uncertainty Principle (in its energy-time form).
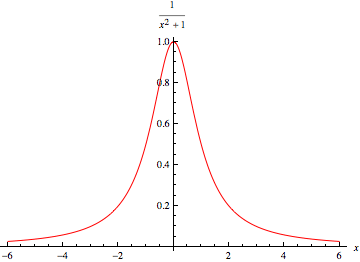However, the analogy is imprecise since the snapshot is more likely to show the hand at one of the extrema of the oscillation range (where it stops and inverts its motion) rather than at the center (which it passes with the highest speed). On the contrary, the mass at which we observe a unstable particle is most likely the natural mass, and it distributes according to a Lorenzian distribution, such as the one shown on the right. Also, notice that the Lorenzian does not have a "range" of masses: a top quark can be found with mass arbitrarily close to zero, albeit with very small probability.Back to the measurement
Anyway now let us go back to the actual measurement of the top quark, which is a combination of several different results obtained by the two collaborations from their analysis of about half the data they collected since the start of Run II at the Tevatron. If you ask whether they will one day add the rest of the data and produce a yet more precise number, my answer is "probably not". The reason is that it takes a lot of effort to produce these measurements, and the statistical uncertainty of each independent measurement is now generally not the limiting factor - systematic uncertainties have grown more important with the accumulation of data.
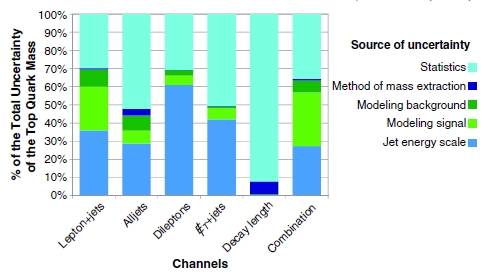The graph on the right shows the breakdown of the uncertainty estimated to come from the different sources: statistics, jet energy scale, and other systematics - mostly connected to modeling assumptions. You see clearly that the data size is adequate, and statistics is no longer a limitation, except for the measurement which relies on the decay length of b-quarks emitted in top decay (second to last bar).The combination is performed by accounting for correlated uncertainties across the various channels using a statistical method on which I do not wish to focus today. The result is that the top mass weighs 173.18 +- 0.56 (stat) +- 0.75 (syst) GeV: a 0.54% total error if you add statistical and systematic uncertainties in quadrature. This is a wonderful achievement for the Tevatron experiments and a true legacy of the machine. Note also that the statistical error is significantly smaller than the total systematic error, confirming what I was saying above about the relative importance of future addition of data.
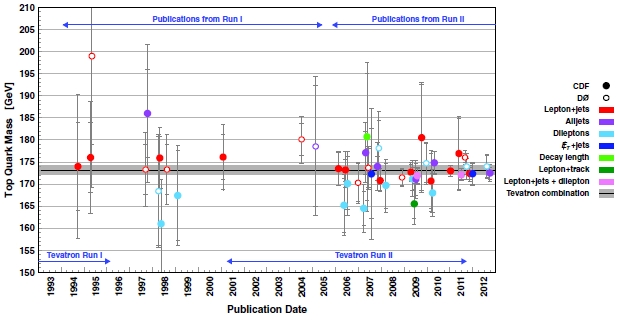
In the paper you also find the very nice picture above, which shows the progress in top quark mass measurements by CDF and DZERO as a function of time. By looking at this graph I cannot fail to notice how CDF determinations in the lepton plus jet category - the full red points - have consistently been aligned very well with the now precisely known value of the top mass. Among these is the very first measurement, the 1994 one, which was performed by CDF when the top quark had not yet officially "discovered" (the significance of the observed excess being smaller than 5 standard deviations). Back then CDF measured M_top = 174 GeV, with a large error driven not only by statistics (only seven events were available back then!), but by a conservative assessment of systematics. Well done, folks!
Comments