Despite the shutdown of the Fermilab Tevatron collider, two years ago, and the subsequent disassembling of the glorious CDF detector, the CDF Collaboration continues to produce excellent physics results using the large bounty of data they have accumulated in the course of the past 10 years.

Today you can find in the Cornell arxiv a new paper by CDF, which describes a new very interesting measurement of a property of the top quark - the particle discovered at Fermilab in 1995, the heaviest known elementary particle we know. The property measured is the lifetime of top quarks.

Because top quarks are exceptionally heavy - 173.3 GeV, give or take less than a GeV - they have a large amount of energy to impart to their decay products, and this has several consequences; one of these is their quite ephemeral nature. Theoretical calculations allow us to predict that for such an object the lifetime depends on the inverse of the third power of the mass, yielding a very short existence for top quarks - less than a trillionth of a trillionth of a second !

Even imagining such a short time interval is a challenge. Light quanta do not even manage to travel through a proton in 10^-24 seconds. How to picture it ? Let's say that if you could travel from here to the center of the Andromeda galaxy in one second (forgetting the limits of special relativity for a moment), a top quark created when you start that quite fast journey would decay before you move by one millimeter !

If you stop and think about this for a minute, it becomes increasingly awesome to realize that physicists can even measure such a short time interval. Yet we can. That is because the lifetime of a particle is inversely proportional to their natural width. The natural width of a resonance is the intrinsic uncertainty on their rest mass. The two quantities are connected by Heisenberg's uncertainty principle, expressed in the energy*time relation ΔE * Δt > h/2π, where h is Planck's constant.

The uncertainty relation connects the time duration of the resonant process (the life of a subnuclear particle)  Δt to the uncertainty in its rest energy - or mass - ΔE. Their product must exceed the reduced Planck constant, so the smaller Δt, the larger must ΔE be. But what does it all really mean ?

Let us think at the vibration of a string. It produces a sound, which is audible if the vibration has a frequency exceeding some 40 Hz and less than some thousand Hertz. If we imagine hearing a very low note for a very short interval of time, we will have a hard time deciding what was its exact pitch: that is because we only heard few oscillations of the wave. In some sense, the pitch becomes undetermined if the duration of the note is short enough that not enough maxima are produced in the acoustic wave.

Elementary particles are not different - in fact, all oscillatory phenomena share the basic phenomenology in this respect. So a top quark living less than a trillionth of a trillionth of a second does not manage to "consolidate" into a well-defined pitch. The resulting uncertainty can be observed because we can measure the mass of top quarks, and we can in principle determine that some of them had masses slightly above or below the average. The spread of masses is thus connected to the lifetime of the particle.

The CDF collaboration produced exactly that kind of measurement. Of course, since we are talking about a spread of the order of 1.5 GeV, this is a difficult measurement to perform: the problem is that the mass of any one top quark is only measured with a precision one order of magnitude larger - 10, 20 GeV depending on the particular characteristics of the observed decay. Our particle detectors are excellent devices, but their energy resolution is not good enough to go below that level. On a statistical basis, however, we can detect whether a sample of top quarks all had the same rest mass or slightly different ones, by studying in detail the distribution of reconstructed masses.

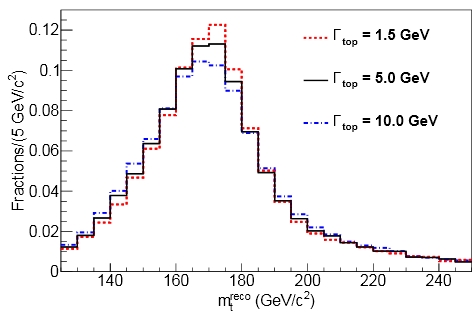In the figure on the right you can see how the reconstructed mass distribution of simulated top quarks would change if we assumed a width of 1.5 GeV, or 5 GeV, or 10 GeV. The difference is tiny ! Yet with large samples of reconstructed top quarks one may fit the observed distribution to different hypotheses, and get a confidence interval on the top quark width. Of course, this is easier said than done: one must first isolate a clean sample of top quarks, then operate a careful reconstruction of the mass, and then the fit will have to account for backgrounds.

The result of fitting the data sample to different width hypotheses is shown in the figure below. This is what is called a "confidence belt": for every value of the measured width (on the horizontal axis), one may determine a confidence interval (on the vertical axis) which would contain the true value of the top width a given percentage of the times, if the experiment were repeated many times. The actual measurement is shown by a vertical arrow: this sets the confidence interval for the true top width at 1.10 < Γ < 4.05 GeV (at 68% C.L.).



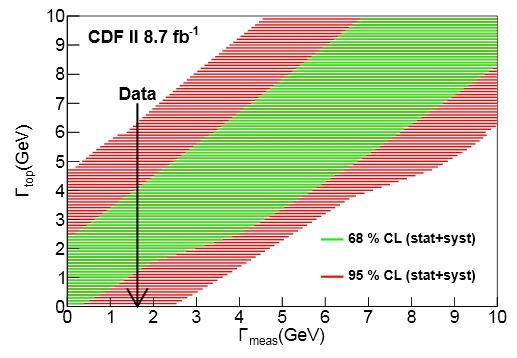
It is necessary to say that this is not the first determination of the top quark width; both CDF and DZERO have produced such measurements in the past; DZERO, using some model-dependent assumptions, has produced a result more precise than the one described here. The one by CDF is however less affected by theoretical assumptions.