The W boson, like any unstable subatomic particle, has a very short lifetime, which depends on the strength of its couplings to lighter particles, on its own mass (generally the heavier a particle is, the faster is its disintegration), and on the availability of lighter bodies into which to decay without breaking any fundamental rule.
In the case of the W, the mass is quite large (80.4 GeV), so we rightfully expect that its decay be fast. The interaction which provides the conversion to ligher bodies is the electroweak one: the W is not coloured, so quantum chromodynamics has no business in its phenomenology. And the final state bodies are in turn all conceivable pairs of fermions which have a total electric charge equal to that of the W: both lepton pairs and quark pairs are allowed. For leptons this boils down to an electron-electron neutrino pair, or a muon-muon neutrino pair, or a tauon-tau neutrino pair; for quarks, we have up-antidown, or charm-antistrange pairs; top-antibottom pairs are forbidden because the top quark is far heavier than the W!
All in all, we have three possible leptonic decays, and six possible quark decays: that is because quarks have to be counted three times each, since they may have different colour charge. Now, just a little electroweak theory would be enough for you to compute the lifetime of the W boson, given its mass and the knowledge that it may decay to nine possible fermion pair combinations. However, if you admit you cannot do it, be my guest, since I have forgotten how to compute the W lifetime myself... But culture is what remains when one forgets what he's once learned the hard way!
So let us forget about details, and just state the result: the W boson lives an astonishingly short lifetime, of the order of a millionth of a billionth of a billionth of a second - a time so short that it is really hard to describe it. I think I am not even going to try!
But how do we measure a time so astonishingly short ? Well, we physicists are tricky guys. We know that the lifetime of a particle is inversely proportional to another parameter which is easier to measure, the width. The width of a particle is the spread of possible mass values it can assume: if you reconstructed perfectly the mass of a thousand W bosons, you would not come up with a single value 1000 times, but rather with a distribution following a curve, called Breit-Wigner; a curve endowed with a single meaningful parameter besides its mean value: the width. The fatter the curve, the shorter the lifetime.
Such a connection is not too hard to understand: if you strike a very low note on a piano for a very short time, you will be able to hear only a few oscillations of its pitch, and thus you will be unable to tell very precisely what tone it is. The shorter the time a particle lives, the less defined is its own rest mass - hence the connection that we can use to determine the lifetime.
With W bosons, the matter is complicated experimentally by the fact that the particle has a 2 GeV width, but its mass is usually determined with a much coarser resolution: we usually end up with mass distributions that have an observed width of several GeV, and most of this observed width is due to the experimental precision with which we measure the energy of the final state bodies into which the W has decayed. However, there is a trick we can use -another one!
What we can do is to watch the mass distribution far away from the peak! This helps because the Breit-Wigner has longer tails than the Gaussian curve that usually is caused by the energy resolution. By going where the resolution effects have died out, we can indeed measure the W width from the shape of the tail! In other words, at the peak we observe the convolution of a Breit Wigner and a Gaussian, while far away we measure something much closer to the original Breit-Wigner shape.
The method has been used by both CDF and DZERO, the competing experiments at the Tevatron proton-antiproton collider, and the two have produced equally sensitive measurements of the total W boson width. This turns out to be in excellent agreement with the Standard Model, and the measurement also beats by far the combined measurement of the LEP II experiments.
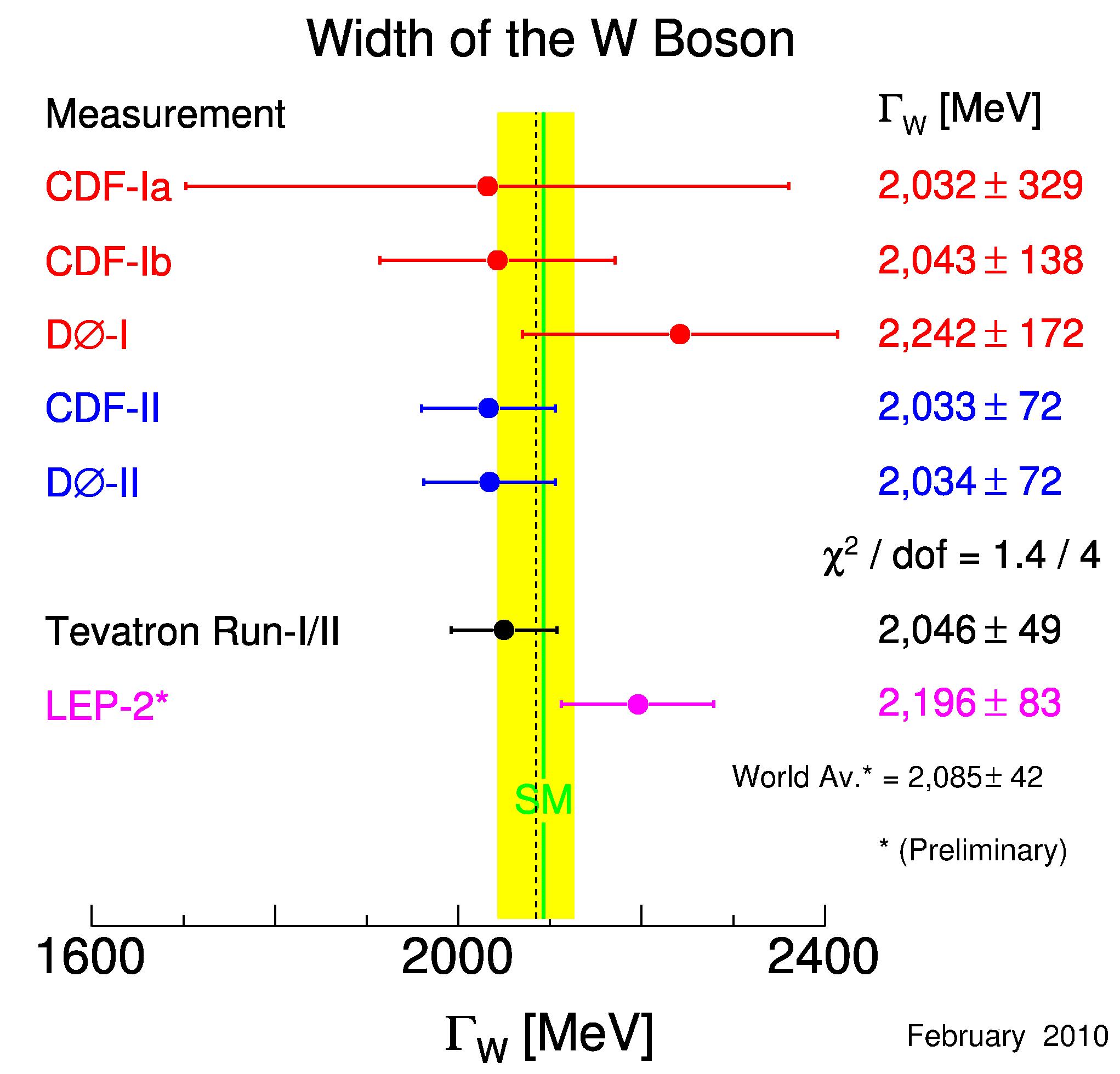
Above you can see all the recent determinations of the W boson width. You can clearly see that all measurements are in agreement with Standard Model predictions. You also see that the new Tevatron average of CDF and DZERO results (2,046+-49 MeV, the black point) is almost two times more precise than that of the W-boson factory per excellence, LEP II (the purple point at the bottom). Not bad! Go Tevatron!
For a description of the combination between the CDF and DZERO W width results, please see the article here.





Comments