John asks whether it is possible that what we see, when we plot the mass of a particle, is the true distribution of values of the particle - i.e. that the particle does not have only one mass, but a distribution of values. The question is not an idle one! So let us discuss it below. I will make a few points to clarify matters.
1. We estimate by proxy
What we calculate in experiments when we reconstruct the mass of a particle from the products of its decay is *not* the mass; rather, it is an *estimator* of that fundamental parameter. The estimator, if unbiased, distributes with a narrow (or less narrow, if resolution is worse) shape around the true value of the particle mass. The distribution is usually a Gaussian because of experimental resolution on the energy and directions of the decay products: the small imprecisions in the measurement of those quantities "add up" into a Gaussian spread, as dictated by the central limit theorem.
2. What is the true mass?
Subnuclear particles, even the elementary ones that John mentions in his question (quarks and leptons, and I guess Higgs bosons, as the original article included a graph of a Higgs mass distribution) may have a finite lifetime. This is true for all but very few of them (the electron and the photon, and also the up quark, albeit for the latter things are complicated by the QCD interaction which we cannot disentangle from the quark's behavior).
Particles that are perfectly stable (and so have infinite lifetime), like the electron, do have a perfectly defined value of mass. So if you could measure the electron mass with infinite precision, you would be certain to obtain always the same value; if instead your measurement were affected by resolution effects, you would obtain a distribution of measurements whose shape would reflect the cumulative effect of your measurement errors - a Gaussian shape, more or less (we could predict that this is not a Gaussian in some particular cases, but I will gloss over this detail).
In contrast, all particles with a finite lifetime are indeed created with a *distribution* of true masses, which has a Breit-Wigner shape. The Breit-Wigner is also called Lorenzian, or Cauchy distribution. It is a sort of peaked structure with long tails, and it has the interesting feature that from a mathematical point of view the mean is undefined, and the width is infinite! Yet experimental physicists are not bothered by these abstract issues, and they work with the Breit-Wigner without worries.
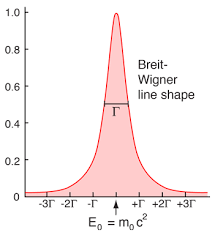
Also note - the support of the Breit-Wigner is the full real axis, but for us speaking of a negative mass is absurd; on the other hand, a produced mass which is larger than the total collision energy is also physically impossible. So the Breit-Wigner is nothing more than a representation of the properties of the resonance "near" the nominal value of its mass (the "peak" of the distribution). [Yet, the shape of that curve has been used in recent times by studying it at mass values much larger than the nominal mass, but still much lower than the total collision energy.]
The width of the Breit-Wigner distribution is governed by the "natural width" parameter Gamma, which is essentially the inverse of the particle lifetime. The shorter the lifetime, the larger Gamma is. So, for all but the stable particles, John is (partly) correct - they do have a distribution; but this is not, typically, what we see, because of mentioned resolution effects!
The shape of the Breit-Wigner distribution, and the spread of "true" masses that correspond to it, is an effect of Heisenberg's Uncertainty Principle. In a nutshell, the mass of a particle corresponds to the energy of the state at rest, and energy cannot be determined with infinite precision if the particle is only around for a short instant: the smaller the lifetime, the wider the range of masses that any of the particles of that kind may show.
The phenomenon has a classical analogue in the vibration of a string. If you hit for a brief instant a low key of a piano, you may have a hard time figuring out exactly what note it corresponds to, because the vibration had only a short duration: the vibration phenomenon corresponded to only a small number of wavelengths - say, a dozen of them - and so your ear cannot make it up quite precisely (the lower the tone, the smaller its frequency; the lowest piano keys have a frequency of about 30 Hz). In some sense, the true tone produced by the vibrating string is uncertain, because the vibration did not have time to "settle" to a well-defined frequency.
3. The truth is in the middle
For most elementary particles, which have typically short lifetimes, the mass we can reconstruct when we combine the information from the momenta of their decay products is affected by both effects discussed above - natural width, and experimental resolution. When the former is larger, we observe something close to the "true" distribution, as supposed by John: a Breit-Wigner distribution. More often, natural width and resolution are comparable, and then what we get to see is the mathematical convolution of the Gaussian resolution spread with the natural resonance shape. The convolution is called "Voigtian". Finally, if the resolution effects are much larger than the natural width, we see a Gaussian distribution of reconstructed masses.
Now, the answer to your question is strictly "no" because we cannot avoid resolution errors, so whatever we have at the start (a single value (for all practical purposes), or a distribution of values), our estimator will show a distribution of values that *does not* match the "real" distribution, due to the convolution with resolution effects, which we cannot avoid.
Finally, another detail: in principle, when we produce a particle with collisions that can release a variable amount of energy, as is the case for the protons of the LHC, the prior distribution of energy plays a role in the distribution of masses we see - this follows from the fact that we may be "illuminating" more the left-side of the Breit Wigner distribution more than the right side. At the LHC this is due to the protons being composite objects, and collisions taking place between their constituents, which carry a variable fraction of the proton's energy. In the rest of this article I will skip this detail, but for some broad resonances such as the Z boson this may have a significant effect on the observable distributions.
4. A couple of examples
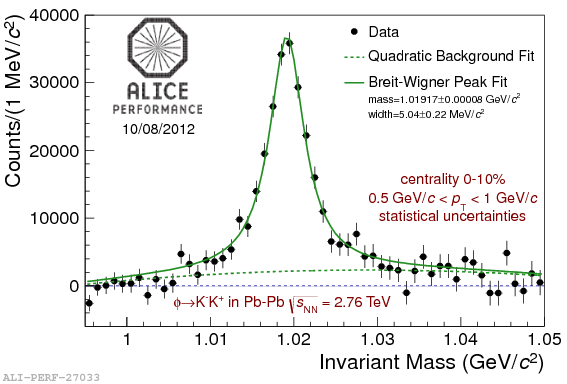
In the graph below you can see what happens when experimental resolution is much smaller than the natural width of the particle. In this case, we are looking at the distribution of reconstructed masses of Phi mesons. The Phi is a composite hadron made up of a strange and an anti-strange quark, and its natural width is of about 5 MeV. Since in this case the particle was reconstructed from detected kaons of small momentum, with a corresponding very small experimental resolution, that factor does not significantly smear the Breit-Wigner distribution, which we get to see in its entirety. The data in this graph was obtained by the ALICE experiment at the CERN LHC, from lead-lead collisions. Note that the shape of the black points is affected by some uncertainty in the background model, so the shape strictly speaking is the sum of the Breit-Wigner and that unknown background.
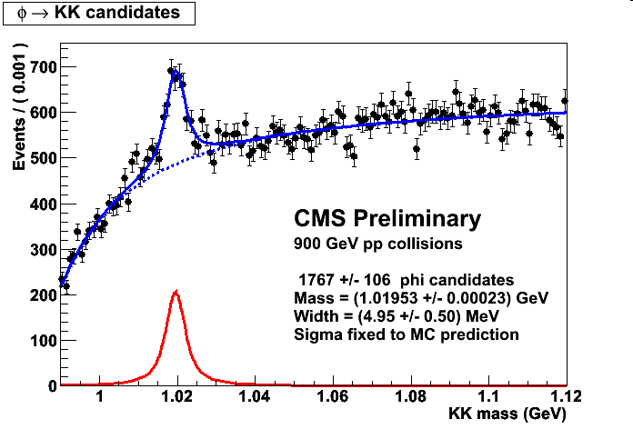
An example of the intermediate case can be made by using the same particle, as seen by data collected by the CMS experiment in 2010. Back then, the LHC had just started to deliver collisions at a small center-of-mass energy, and experimentalists were busy rediscovering known particles in the data, such that they could verify the good calibration of the detector. The graph shows the phi meson peak on top of a large background. This is the result of selecting events that contain two charged particles that look like kaons. The kaon is a hadron heavier than the pion (which is the most abundant particle you get in proton-proton collisions), and this makes it interact differently in the silicon layers of the CMS tracker. This results in a different amount of ionization charge, which allows us to separate it from pions. The Phi peak in the figure is wider than the natural width, and it is indeed well fit by a Voigt distribution.
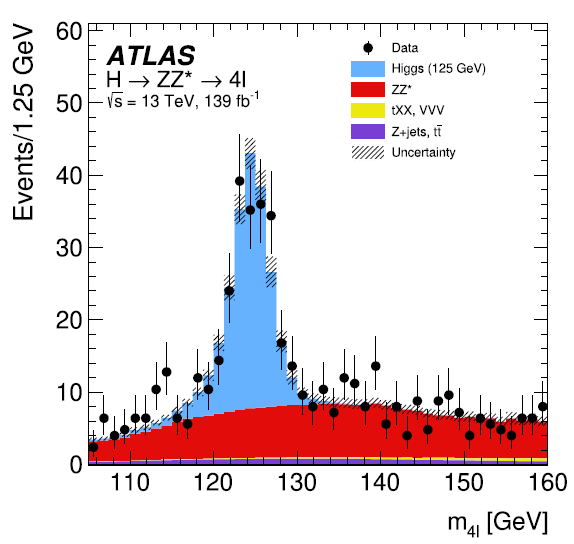
An example of a resolution-driven particle mass peak is instead the one shown below. In this case we are reconstructing Higgs bosons with the ATLAS detector. As the natural width of the Higgs boson is of 4 MeV, while the experimental resolution is three orders of magnitude larger (as the Higgs boson is very massive, the energy of its decay products is large, and so is the absolute uncertainty, which results in uncertainty in the reconstructed Higgs mass), what we see is a Gaussian distribution.
Conclusions
In conclusion, the answer to John's questions is: strictly speaking, no: we always see experimental distributions that to a lesser or greater extent are impacted by the precision of our instruments. However, in some cases this has negligible effect; then, we do see the original distribution of masses.





Comments