This very short paper resolves the matter of black hole firewalls by computing the approximate temperature of a Planck mass black hole. Based on previously published work on black hole temperature I present a precise prediction of the temperature of the Hawking radiation in this situation. The quantum that collapses into the black hole experiences a temperature of 1.410 septillion kelvin. This high temperature would last for about one Planck time. This certainly qualifies as a firewall.
The specific variant of a relativized quantum field theory I used is called the relativized extended standard model. A grand review of this approach is being submitted to traditional paywalled journals. Mostly due to the sociological fact many physicists will either ignore or "forget" to cite papers that are published outside the confines of such venues (Some even refuse to cite the arXiv paper number of peer reviewed, published, but paywalled articles). Secondarily citations pointing from paywalled traditional papers to open access open peer reviewed sources will force people to acknowledge such sources. Which is odd since everyone reads sources like that, certainly the arXiv which is indexed by many research databases.
Introduction
Several papers have been published arguing for and against black hole firewalls. The idea is that as a pair of entangled particles fall into a black hole the entanglement is broken. This releases a great amount of energy as heat. (D.N. Page 1993) (D. N. Page 1993) (Almheiri, Marolf, et al., Black holes: complementarity or firewalls? 2013) (Almheiri, Marolf, et al., An apologia forfirewalls 2013)
Using the relativized extended standard model (Farmer, Fundamentals of Relativization II with Computational Analyses 2015) (Farmer, Gravity Mediated Interaction Cross Sections Without Ultraviolet Divergence. 2015) and a calculation of black hole temperature (Farmer, Fundamentals of Relativization II with Computational Analyses 2015)I will compute the temperature of a Planck scale black hole.
The reason to consider quantum black holes is that theoretically any quantum falling into a black hole will, as it crosses the horizon, gain enough energy that itself will collapse into a quantum black hole. The decay of this quantum black hole by way of Hawking type radiation will tell us about the existence of firewalls.
Suppose a high energy pure state collapses to form a Planck scale black hole. Rather than speculate on it I can calculate about it. In a previous paper I gave an approximate relationship for black hole luminosity and temperature as a function of mass. This relationship unlike that of Hawking is based on a framework that unifies quantum field theory with relativity by making QFT more relativistic, it is called relativization. (Farmer, Quantum Gravity: Have We Been Asking The Right Question? 2015)
Concept.
A simple view of Hawking radiation would be as follows. A quantum interacts with another quantum and becomes entangled. One of the quanta falls into a black hole and as it falls it gains energy, the wavelength shortens and just as it hits the event horizon, it collapses into a quantum black hole. About one Planck time after the formation of this quantum black hole it decays via Hawking radiation into a thermal spectrum of quanta of all kinds at a very high temperature.
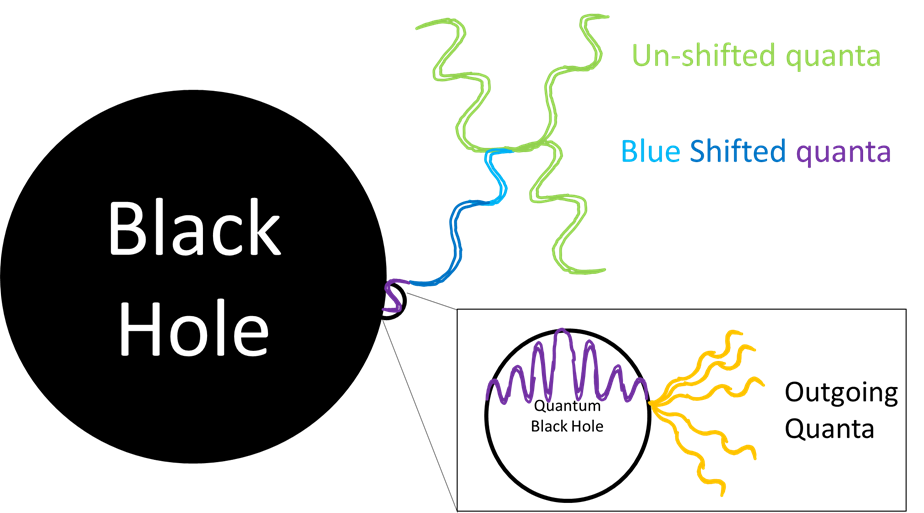
Figure 1: A simple view of Hawking radiation. A quantum, here represented as spin 2 bosons, interacts with another quantum and becomes entangled. One of the quanta falls into a black hole and as it falls it gains energy, the wavelength shortens and just as it hits the event horizon, it collapses into a quantum black hole. Inset, about one Planck time after the formation of this quantum black hole it decays via Hawking radiation into a thermal spectrum of quanta of all kinds at a very high temperature.
Calculations
The calculation that is needed will rely on previously published work which told me the luminosity and temperature of a black hole. The key equations are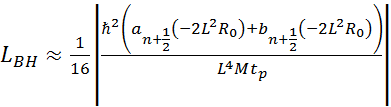
which gives the luminosity of a black hole of mass M, where L is the Schwarzschild radius of the black hole, R0is a constant space-time curvature assumed equal to the cosmological constant, and tp is the Planck time. The other key equation relates luminosity to temperature.
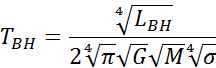
The only new constant is σ which is Stefan’s constant. Calculations are done in the Mathematica notebook which accompanies this paper. The firewall temperature works out to

In words that is 1.410 septillion Kelvin. That is a firewall by any definition.
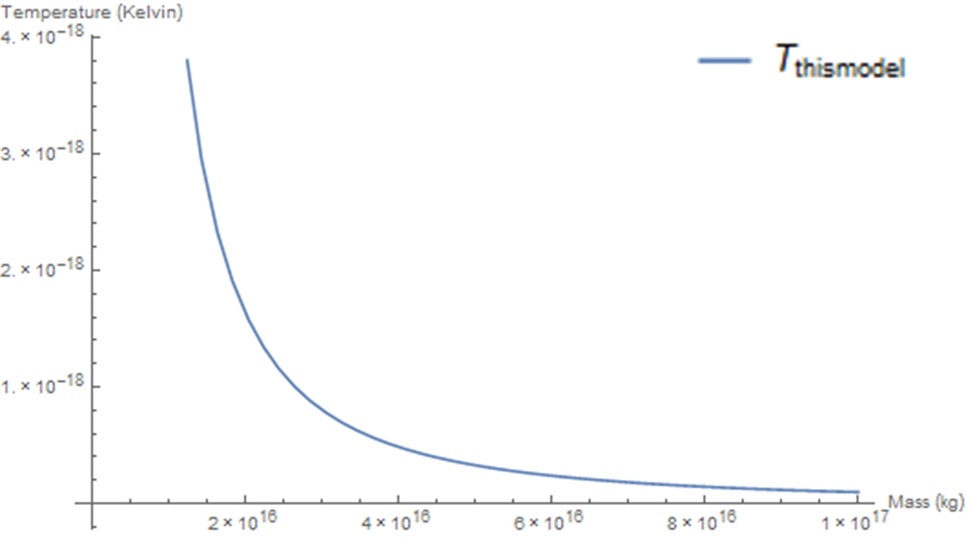
Figure 2: A plot of black hole temperature with respect to mass. Notice two things about this graph. First, as the mass decreases the temperature increases markedly. Second, for black holes well below a stellar mass their temperatures are well below that of the CMB. The firewall phenomena only exist because as individual quanta are pulled in they temporarily form a quantum black hole due to the aforementioned blue shift then radiate away most of their energy. On average, at the macroscopic level, any black hole you encounter will appear colder than ice until you contact it.
Conclusion
What causes the firewall is that as the in falling quantum enters the hole it gains enough energy to collapse into a quantum black hole and then radiates at an incredible temperature. The in falling pure state transforms into a mixed state. The entanglement between the outgoing pure state and any one quantum of this radiation would be minimal if any (Yang 2006) but not zero since the number of quanta emitted would be finite. So information can be preserved even with firewalls as hot as 1.410 septillion kelvin.
The problem is as soon as any of the Hawking radiation particles interact with anything else that information would be gone. What is known in the literature as the monogamy of entanglement says that only two systems can be maximally entangled. The degree of entanglement decreases precipitously for numbers of systems greater than two. It does not become zero the information is still there but, like a shredded and burned newspaper it would be impractical for all but a God to retrieve it. Even in theory.
References
Almheiri, Ahmed, Donald Marolf, Joseph Polchinski, and James Sully. 2013. "Black holes: complementarity or firewalls?" Journal of High Energy Physics, Volume.doi:10.1007/JHEP02(2013)062.
Almheiri, Ahmed, Donald Marolf, Joseph Polchinski, Douglas Stanford, and James Sully. 2013. "An apologia for firewalls." Journal of High Energy Physics 2013. doi:10.1007/JHEP09(2013)018.
Chowdhury, Borum D, and Andrea Phum. 2013. "Decoherence and the fate of an infalling wave packet: Is Alice burning or fuzzing?" Physical Review D 88 (6): 7. doi:10.1103/PhysRevD.88.063509.
Farmer, Hontas. 2015. "Fundamentals of Relativization II with Computational Analyses." The Winnower (The Winnower).doi:10.15200/winn.144503.33399 .
Farmer, Hontas. 2015. "Gravity Mediated Interaction Cross Sections Without Ultraviolet Divergence." The Winnower.doi:10.15200/winn.144503.33399.
Farmer, Hontas. 2015. "Quantum Gravity: Have We Been Asking The Right Question?" APS April Meeting. Baltimore: American Physical Society. 1. doi:10.13140/RG.2.1.2398.5767.
Page, Don N. 1993. "Average entropy of a subsystem ." Physical Review Letters (American Physical Society) 71 (9): 1291-1294.doi:10.1103/PhysRevLett.71.1291.
Page, Don N. 1993. "Information in black hole radiation." Physical Review Letters (American Physical Society) 71 (23): 3743-3746.doi:10.1103/PhysRevLett.71.3743.
Yang, Dong. 2006. "A simple proof of monogamy of entanglement." Physics Letters A 360: 249-250. doi:10.1016/j.physleta.2006.08.027.
Farmer, Hontas. 2016. "Relativization a Unifying Framework for General Relativity and Quantum Field Theory Without Ultraviolet Divergences." PREPRINT. Research Gate
UPDATE
The paper is now final after a long enough period of review I suppose no one could argue with the hard numerical calculations.
Hontas Farmer, A Simple Calculation That Shows Black Hole Firewalls Exist and How Hot They Are., The Winnower 3:e146254.45957 (2016). DOI: 10.15200/winn.146254.45957
To ensure useful reviews are posted with the paper at The Winnower I will close comments here. Full formal reviews at The Winnower can be done as independent publications with the same academic "credit" for same. This is not without precedent since in printed journals via papers criticizing other papers, and letters to the editor journals have hosted such debate.
Lord knows nothing is more debatable than anything to do with black holes and information.



Comments