A three inch long equation (or according to Kaku one inch) is the holy grail of post modern theoretical physics.  We all want one equation from which one can derive all known physical laws. I don't have that.  What I have today is a three inch equation which goes a step towards unifying gravity and the standard model of particle physics.  It will allow one to predict the gravitational corrections to standard model interactions. Not only do I have a theory to present, but an experiment to propose which could test this theory.   A test in this universe, not some multiverse, landscape, or anything else like that.   

 Gravity, the most familiar force in all of nature has proven to be the most mysterious at length scales comparable to that of the atom and smaller.  

Those lengths are the domain of Quantum Mechanics and Quantum Field Theory.  Gravity, the force that binds planets to stars and forms large scale cosmological structure would have lived at the sub atomic scale at times near the big bang.  Tiny fluctuations in the stat e of the universe at that time, stretched out to become and set the stage for, the formation of large scale structures and ultimately life itself.  To understand the universe humanity must understand gravity at those length scales. 

The most researched direction for understanding gravity at the very small sub atomic length scales is generally known as “Quantum Gravity”. There are several major directions in Quantum Gravity, String/Mbrane  Theory and Loop Quantum Gravity.  There are others but those are the most popular and LQG is a distant second.  The basic concept underlying both of those models is that at the most fundamental level General Relativity needs to be modified in order to work with Quantum Field Theory.  In other words gravity needs to be quantized.

The model I discussed on this blog, published at TheWinnower in a series of papers, and discussed at the April 2015 APS meeting takes a fundamentally different approach.  Instead of quantization we take Quantum Field Theory and modify it so it fits within the world of General Relativity. The word I borrowed for this process is “Relativization”.  That is making a theory comply with the prescripts of Special and General Relativity.  The model I have devised is one preliminary method of relativizing a theory.  Yet, it has yielded up results that no other model can match.

1. I have shown that this model can reproduce Hawking Radiation and gives a relationship between black hole temperature and mass which is the same shape as that of Hawking's model.  In this model black holes neither explode right away or are impossible to form.    
2. I have shown in the paper I am going to detail now that interaction cross sections can be computed without UV divergence in this model.  Based on that calculation I have outlined a conceptually simple experiment.  

Gravitational cross sections without UV divergences and the three-inch equation.

I will spare this popular account of a whole plethora of equations and present just one. This equation gives the gravitationally corrected interaction cross section for Standard Model particles and fields in terms of generating functional formalism.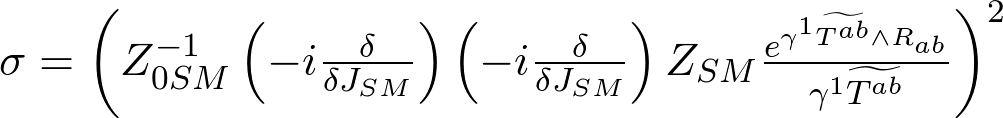

That is a deceptively simple looking equation but it gives the change in probability of a interaction based on gravitational effects.  

Z0SM means the generating functional without interactions for the standard model of particle physics.  JSM is the current of the standard model particles we are concerned with, and ZSM is the generating functional for the standard model including the interaction and the non interaction.  The stress energy tensor written with the \widetilde over it is an integral of the stress energy tensor, and R_ab is the curvature.  The use of Latin instead of Greek indices indicates these are in terms of locally flat coordinates.  The operator R_ab gives as its eigenvalues the local space time curvature which is itself also a functional of the standard model particles and fields in addition to gravity.  The mathematical details are available on The Winnower and Research Gate.

The bottom line: The probability of interactions expressed there as a cross section is a normalize able number.

When this is expanded out as a Taylor series  the gravitational corrections are so small that they would be negligible in most any experiment done to date.    

Hypothetically the effect would appear as a slight difference in interaction cross section with distance from a strong center of mass.  In other words if one were to elevate an atomic clock or a sample of radioactive material by a tiny amount… less than a millimeter and measure the rate of decay, then do that after elevating the sample again, and again… the effect should be a small deviation from what we would predict from gravitational time dilation alone.   

To perform such an experiment, the apparatus would need to be isolated on an optics table, and left to run in a room kept at a very cool temperature, sealed off to run remotely and set up to produce almost no extraneous vibration.  Even then if there is an effect to observe it would be a tiny effect.  Any effect of any theory claiming to address gravity at these length scales should be tiny.  One could spend a lifetime working on just that one experiment.   

Such work I will leave for others for the time being.

Right now I have teaching to prepare to do, and union organizing to do.  

The City Colleges of Chicago Librarians and Contingent Faculty union (CCCLOC) is in the midst of contract negotiations.  We are almost the lowest paid such faculty in the area of Illinois near Chicago.  Yet, we have to live and work in the city of Chicago and/or its nearby suburbs with all the associated cost on an income which is less than the United States of America’s federal minimum.  It is hard to care about combining GR and QFT when one has to worry about paying the bills.