I've often used baseball to talk about concepts such as drag, the Bernoulli principle, Reynolds number and the Magnus effect but Beckham's ability to curve the football so much can teach the same things.
The Bernoulli effect tells us faster moving air reduces pressure and a pressure difference is on either side of the ball creates a net force called the Magnus effect:
Velocity
 Drag
Drag


The force due to the Magnus effect, the lift force, is stated as
FL = CLρD3fv
CL is the lift coefficient
ρ is the density of the air (1.20 kgm−3 at sea level),
D is the diameter of the ball - circumference between 0.68 and 0.70 m, so assume a diameter of 0.22 m)
f is the spin frequency of the ball
v is the velocity of the ball.
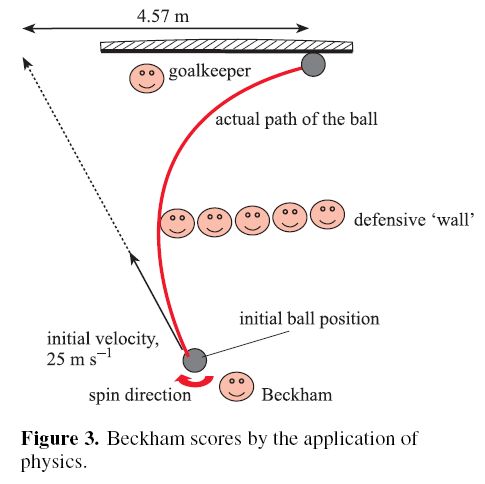
For the World Cup, the Institute of Physics is making free to read the classic Gren Ireson (2001 Phys. Educ. 36 10 http://iopscience.iop.org/0031-9120/36/1/301) piece on how Beckham's kick works. It's worth reading even if Beckham is out with an injury and rather long in the tooth (hey, I am wearing my Thierry Henry shirt during this France-Uruguay match and he may never step on the field) because good physics is always relevant.
Also, take a look at "Soccer: Is scoring goals a predictable Poissonian process?" (2010 EPL 89 38007 doi: 10.1209/0295-5075/89/38007) which uses finite-size scaling to make football games independent Poissonian processes with pre-determined expectation values. Sure, lots of studies have been done on the behavior of spectators, the statistical vs. systematic features behind
league tables and the temporal sequence of ball movements but this tackles (ha ha) scoring itself.
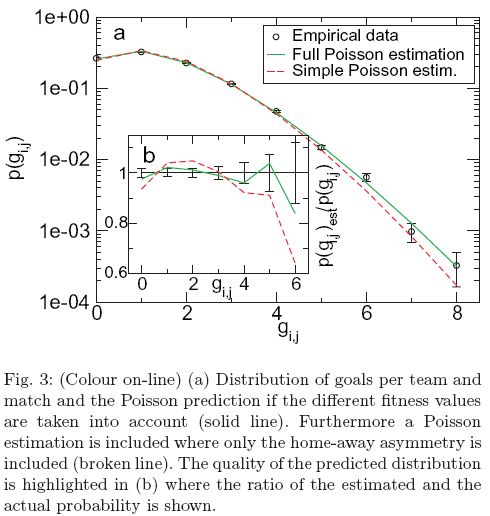
The conclusion? If you factor out the minor differences between a Poissonian and binomial distribution and the tendency towards a draw, a soccer match is pretty much equivalent to two teams throwing dice.
Need even more proof physicists love football? Check out this nifty collection of IOP articles on how the game works, available free of charge (during the World Cup, anyway).




Comments