Bell's Future Quantum Mechanics - A Novel Interpretation

Hello! Years and years have gone by without a blog. For reasons I do not understand, I appear to...

Future Train Wreck: Mine or Modern Physics talk Next Thursday, Jan. 26

If you are in Cambridge, MA on Thursday, Jan. 26, you can see me live at MIT in room 3-270 from...

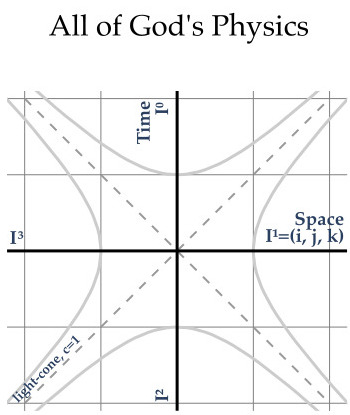
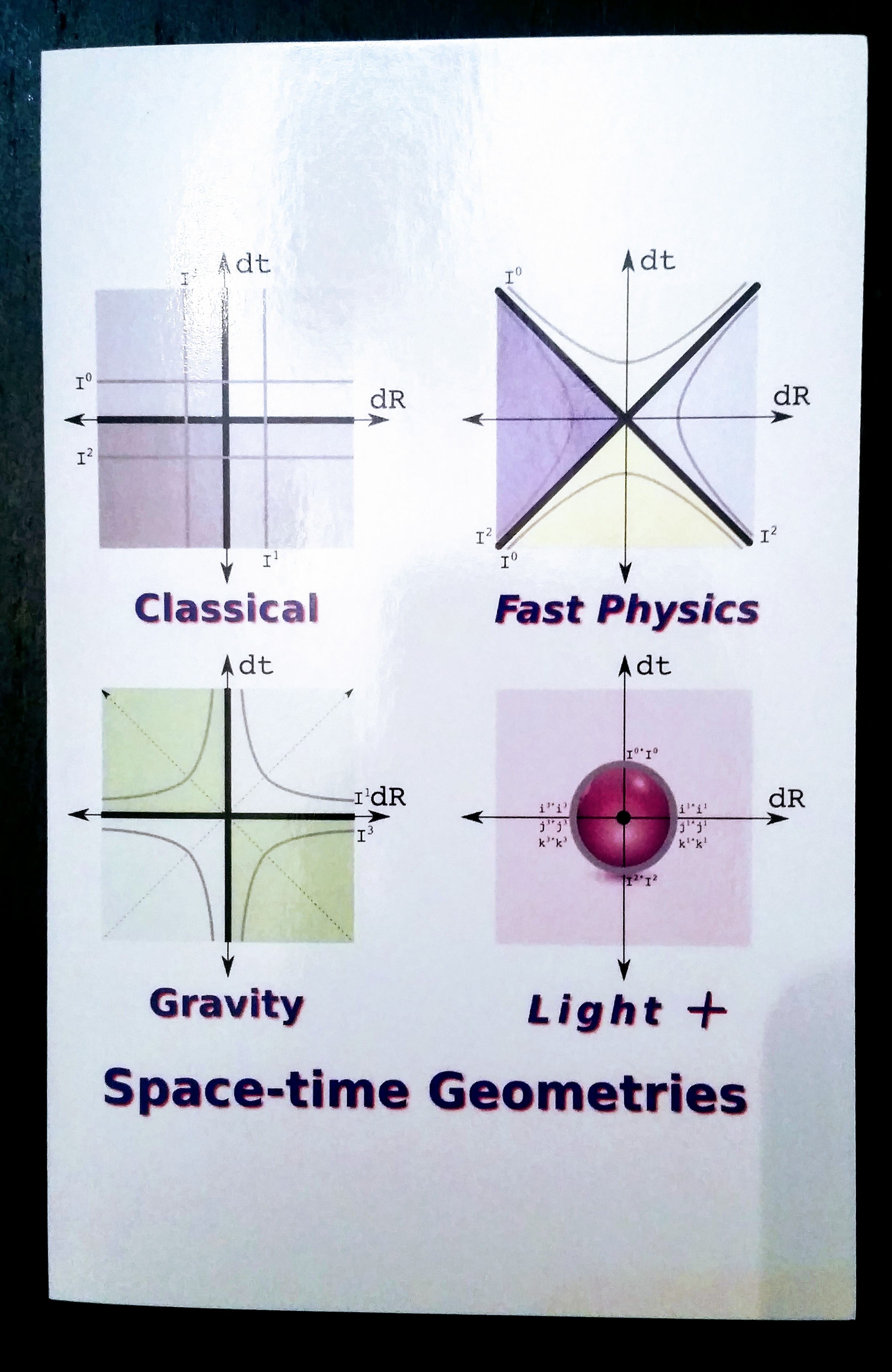Holiday Physics Card, 2016

Just put them in the mail on December 24...It was a fun year of thinking, whether the idea is right...

Unified Mathematical Field Theory Talk

I gave a 15 minute talk at a local Americal Physical Society Meeting. Here is the title and...

Doug Sweetser

Trying to be a semi-pro amateur physicist (yes I accept special relativity is right!). I _had_ my own effort to unify gravity with other forces in Nature. It ran into quite a number of technically... Read More »

A Toy Model For Q<sub>8</sub>

Mar 20 2012 | comment(s)

The idea for this blog was dead simple. In my second blog at Science 2.0, "Quaternions for a Third Grader", I showed of my clay and pipe cleaner model of quaternion multiplication. A few months ago, David Halliday and I started talking about the finite group Q₈, which over the real numbers becomes the quaternions. David pointed out my tetrahedron was half the cube it needed to be to represent Q₈. That was the idea for the blog: make a cube to represent that finite group.

$BFF with HBT (hyperbolic trig)$

BFF with HBT (hyperbolic trig)

Mar 13 2012 | comment(s)

I enjoyed Johannes Koelman's blog, "Velocity: Stuff That Doesn't Add Up." If you haven't read it, please consider doing so. I will review just the math here. There was a technical point that probably flew over many a reader's head. When discussing the elegance of the Lorentz relativity approach, he mentions a hyperbolic tangent. Hyperbolic trig functions used to cause me hypertension. With a little math and a few pictures, gone is my fear. Hopefully the reader will feel these strangers are not so strange after reading this blog.

Galileo Velocity Roundup

$Snark Attack Avoided with Answers$

Snark Attack Avoided with Answers

Mar 06 2012 | comment(s)

Jan. 23, Slit Experiments and Coherence Patterns
Snarky Puzzle

The coherent source is often modeled as a plane wave. Write the quaternion valued plane wave like so:
$\phi = A_0 e^{(\omega t - k \cdot R + \psi)I}$
where
A0 is the amplitude
omega is an angular frequency
k is a wave vector

Diving Into Euler-Lagrange: 2D, 3D, And 4D [parameterizations Of 1D Functionals] (2 Of 2)

Feb 28 2012 | comment(s)

[Title correction: My goal was to create images of 2D, 3D, and 4D functionals. I think I missed that target. Instead I have 1D parameterized curves that all move in up to 3D in space + time. I have a clear idea how to write new code that could move independently with two, three, or four parameters. That code is not written now, so I will change the title to more accurately reflect the content.]

Nothing like writing a title where I am not sure if I can pull it off. It reminds me of skiing slowly off a 6 foot cliff in Colorado. By the time I landed, I was going fast. Nothing like the constant acceleration of gravity.

One, Two, Three D

Diving into Euler-Lagrange: 1D (1 of 2)

Feb 21 2012 | comment(s)

Sophisticated physicists appreciate the dance of abstract symbols. I need to build something. The abstract is more real when made out of clay and pipe cleaners. In this blog on the 1D Euler Lagrange equations, beads (not clay) and pipe cleaners will be used to appreciate this important tool, followed by the same story told with symbols.

[note: I missed my usual self-imposed deadline because I was not able to get the icon bar to appear in Google Chrome on a Mac. The browser Opera worked, so long as I cut and plasted URLs for images and HTML code from codecogs.]

A Tour of the Private Pop Science Art Collection

Feb 14 2012 | comment(s)

The 6 minute YouTube video, available in high def, provides a walking tour of my private Pop Science art collection. One painting spent a summer month in Lancaster, PA as part of a juried show. "Turquoise Einstein" was a hit with the public, but did not win "Best in Show" because it was too happy. Happy art is not serious art.

Most of these piece were created around 1995. Each piece was driven by equations I was pondering about in physics. The math is right, wrong or I don't understand it, but at least it looks good.