[Clarification: I tweaked the title because the focus of this blog was intended to be quite small. While scalars and vectors are used in a dizzying array of areas in many dimensions, quaternions are constrained to work in one plus three dimensions. One could say one plus three equals four, which is true, but I say one plus three because with quaternions, the one has different math properties from the three. What happened in the comments was the first two folks admitted they were looking for a blog with a different subject, one that might have me linking quaternions to objects that transform like 4-vectors. That really is beyond the scope of this blog which doesn't confront how anything transforms.
I spent the day with the family at the zoo, idly thinking about physics, but not enough to blog about it yet. Since it is Memorial Day, a day when one should think about those who gave their lives for our liberty, I considered a war story from my family.
This blog required programming. The basic idea is to have four degrees of freedom for the four parameters living inside a four dimensional quaternion. Four for loops did the trick.
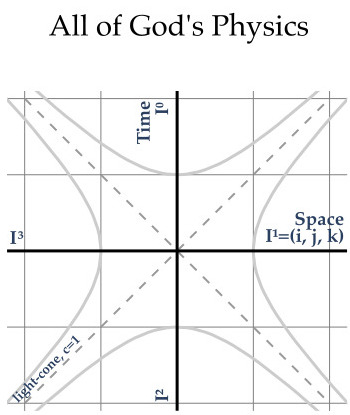 Bell's Future Quantum Mechanics - A Novel Interpretation
Bell's Future Quantum Mechanics - A Novel Interpretation Future Train Wreck: Mine or Modern Physics talk Next Thursday, Jan. 26
Future Train Wreck: Mine or Modern Physics talk Next Thursday, Jan. 26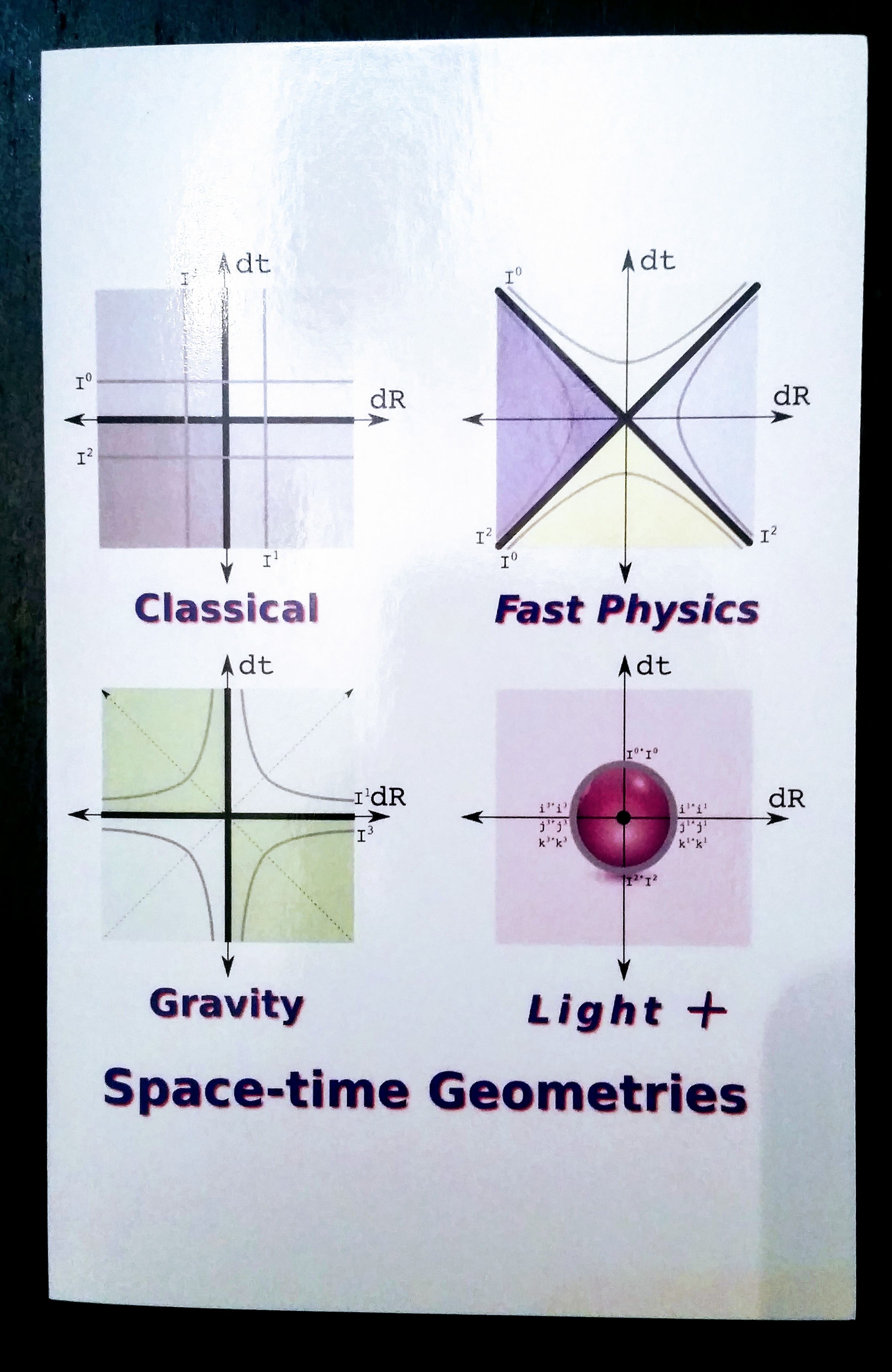 Holiday Physics Card, 2016
Holiday Physics Card, 2016






