Gauge symmetry is a clear, direct idea in EM, as I will detail. This property is essential, [correction: due to redundancy found in the 4-potential description of light and not any issue of the speed of travel for the wave]. Any proposal for gravity must also have [gauge symmetry]. I will show how the Lagrangians I have discussed over the last few months do not have this property, therefore they are wrong. I have altered three titles to say "RETRACTION", including a brief explanation at the start. [Note: the corresponding YouTube video titles have also been marked.] A different Lagrangian I am toying with might have a chance, but that will be discussed at another time.
Click or skip this reading of the blog.
RETRACTION: I have decided to retract three blogs (Deriving … 4/5, 5/5, 6/5+1). I was unable to figure out a reasonable statement concerning gauge symmetry. When the blogs were initially written, I focused on the field equations, mainly the Gauss-like law, and ignored the force equations entirely. Finding a solution that works with the the field and force equations were not looked for. A consistent proposal should do all three things (fields, forces, and solutions) with grace. I have concluded it is not possible to achieve these goals with the Lagrangian as written, hence the retraction.
The hypercomplex gravity and unified GEM Lagrange densities was wrong.

Gravity continues to work fine, even though we don't know why. Newton wrote down the first calculus based description. Gravity worked at a distance for reasons beyond our reach. Einstein developed a more accurate description with a little help from his friends, including Grossman, Hilbert and Schwarzschild. "Matter tells space how to warp. And warped space tells matter how to move" is John Wheeler's circular logic jerk. My own work suggests gravity is all about doing close to absolutely nothing, pushed to do trivial harmonic motions because there is other stuff in the Universe.
The sixth Snarky Puzzle Answers leads off with the story of a minor controversy.
[Click or skip this
video reading on YouTube.]
Two related Snarky Puzzles
September 20, "Deriving the Maxwell Source Equations Using Quaternions (2/5)"
RETRACTION: I have decided to retract three blogs (Deriving … 4/5, 5/5, 6/5+1). I was unable to figure out a reasonable statement concerning gauge symmetry. When the blogs were initially written, I focused on the field equations, mainly the Gauss-like law, and ignored the force equations entirely. Finding a solution that works with the the field and force equations were not looked for. A consistent proposal should do all three things (fields, forces, and solutions) with grace. I have concluded it is not possible to achieve these goals with the Lagrangian as written, hence the retraction.
RETRACTION: I have decided to retract three blogs (Deriving … 4/5, 5/5, 6/5+1). I was unable to figure out a reasonable statement concerning gauge symmetry. When the blogs were initially written, I focused on the field equations, mainly the Gauss-like law, and ignored the force equations entirely. Finding a solution that works with the the field and force equations were not looked for. A consistent proposal should do all three things (fields, forces, and solutions) with grace. I have concluded it is not possible to achieve these goals with the Lagrangian as written, hence the retraction.
 Bell's Future Quantum Mechanics - A Novel Interpretation
Bell's Future Quantum Mechanics - A Novel Interpretation Future Train Wreck: Mine or Modern Physics talk Next Thursday, Jan. 26
Future Train Wreck: Mine or Modern Physics talk Next Thursday, Jan. 26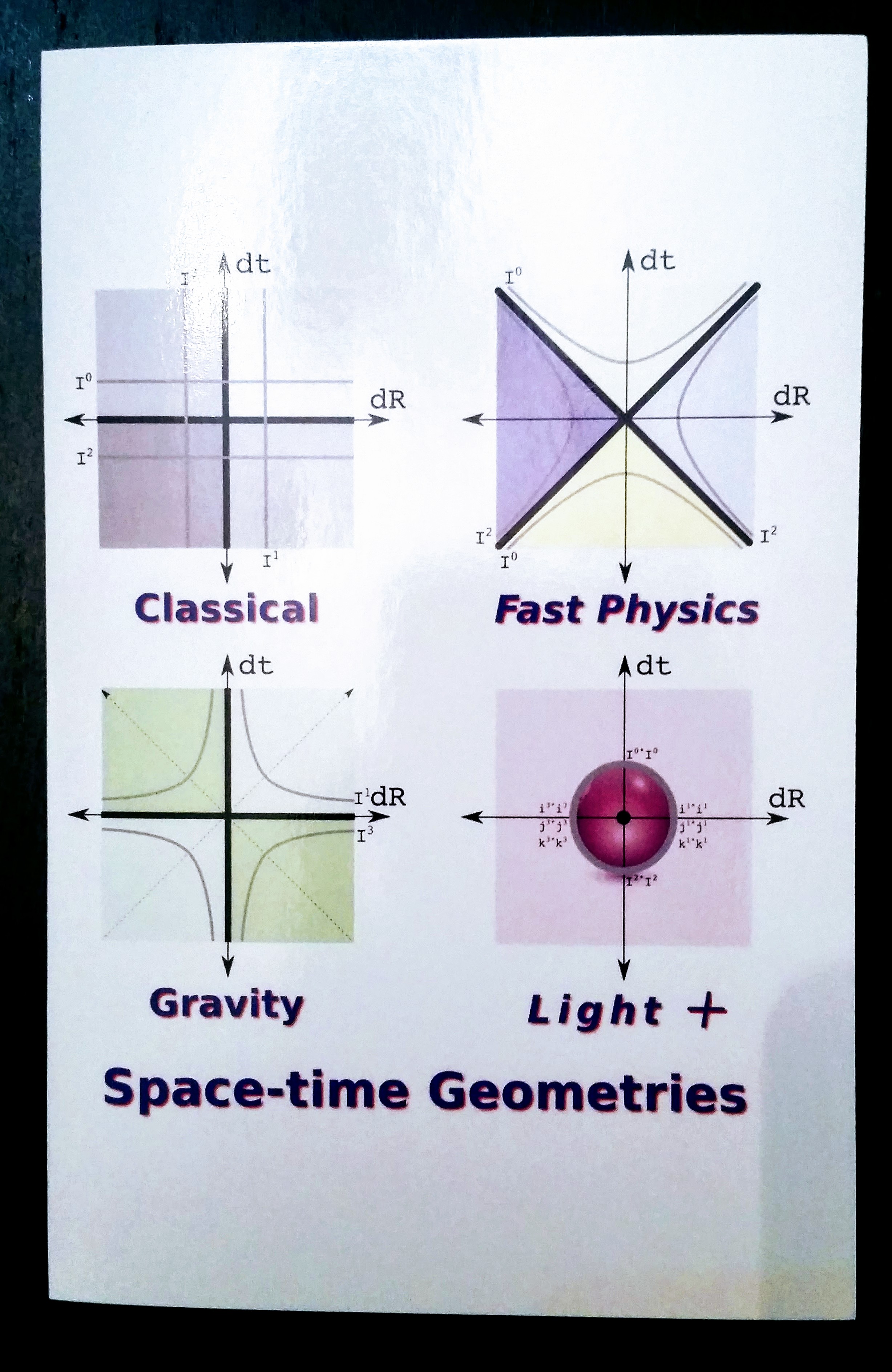 Holiday Physics Card, 2016
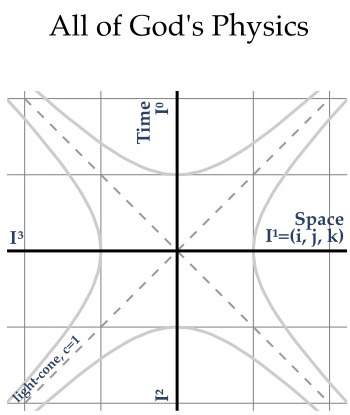
Holiday Physics Card, 2016



 Gravity continues to work fine, even though we don't know why. Newton wrote down the first calculus based description. Gravity worked at a distance for reasons beyond our reach. Einstein developed a more accurate description with a little help from his friends, including Grossman, Hilbert and Schwarzschild. "Matter tells space how to warp. And warped space tells matter how to move" is John Wheeler's circular logic jerk. My own work suggests gravity is all about doing close to absolutely nothing, pushed to do trivial harmonic motions because there is other stuff in the Universe.
Gravity continues to work fine, even though we don't know why. Newton wrote down the first calculus based description. Gravity worked at a distance for reasons beyond our reach. Einstein developed a more accurate description with a little help from his friends, including Grossman, Hilbert and Schwarzschild. "Matter tells space how to warp. And warped space tells matter how to move" is John Wheeler's circular logic jerk. My own work suggests gravity is all about doing close to absolutely nothing, pushed to do trivial harmonic motions because there is other stuff in the Universe. 
