Newtonian mechanics has marked the beginning of a new era for physics. Indeed the newtonian formulation of the gravitational force has allowed to prove the heliocentric theory developped by Copernicus and defended by Galileo. It is a very interesting story that deserve a full post (maybe one day, if I have enough time...).
I'm writing this post because I had to teach to freshmen the foundations of newtonian mechanics. The point is I never liked how formulas were dropped from nowhere when I was a freshman myself. First there was a speach about inertia principle (or newtonian first law of motion), then the teacher would introduce the famous vectorial relation
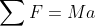
(second law of motion). But the second one was not derived directly from the first one. And yet it is an immediate work.
What is inertia : "The vis insita, or innate force of matter is a power of resisting, by which every body, as much as in it lies, endeavors to preserve in its present state, whether it be of
rest, or of moving uniformly forward in a straight line."
That's how Newton defined it in his Principia. It simply states that an object doesn't change his current motion until it has a good reason, or otherwise,if there's no cause, there is no consequences... Written formally
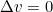
for an isolated object (

being the
velocity of the object considered).
Once Newton introduced infinitesimal calculus, it was easy to formally link the velocity to the acceleration
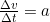
, particularly interesting for non-constant

.
Now, we can notice that any object that is dropped with no speed (
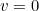
), will start moving under the action of gravity. Before it touches the ground, we have a non-null

. Something acts on it and accelerates it.
For the proportionnality coefficient, one can simply notice that pushing a mass
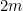
demands twice the force needed to push a mass
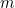
, thus introducing an extensive quantity called inertial mass. Why inertial? simply because it quantifies how much a body resists to a change in its current state. It is easy to illustrate that with a spring and two bodies with the same mass, and a non-frictionnal support. Try to pull one of the bodies with the spring, and then both at the same time, and you'll simply notice that the spring extension will double (the extension of the spring is proportionnal to the force applied).
Finally we end with:
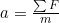
.





Comments