So I started pondering on what exercise I could give to the students. And pretty soon I came up with a nice little game, which I will describe here in case you want to entertain yourself with it. The physics case is the one of detecting and correctly classifying the signal of high-energy cosmic rays hitting our atmosphere and raining down particles on the surface. The SWGO experiment, in particular, is going to be built with a number of Cherenkov tanks laid down in some array on the ground, and it will be tasked to distinguish the signal of energetic photons from the one produced by energetic protons. As both particles create showers of secondary particles on the ground, the distinction is subtle and it relies on detailed properties of the showers and their composition.
Inspired by the SWGO classification problem, I came up with the simple toy problem explained below.
Imagine you have a detector composed of a grid of five by five square positions where active "pixels" can be placed. The grid covers a square area (we could say it is a 5x5 square meter square, or smaller, not relevant here). The task of these pixels, which individually record light hitting their surface in the form of a "Y/N", digital answer, is to collectively determine if the total pattern hitting the grid has one of two possible shapes. The shapes and the grid are shown below.
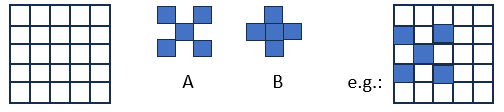
Note that we assume that the patterns are fully contained within the 5x5 grid (a very important detail, as you will realize later). So there is a total of only 9 possible situations with pattern A, and 9 possible situations with pattern B, depending on the location that the 3x3 patterns hit.
As you can see, shapes A and B are both made of five light spots, but they are arranged differently. The question, "How to place a number N of pixels to optimize the discrimination of the two patterns in an optimal way?" is incomplete until we specify what it means to be optimal. Since a set of few active pixels on the grid may or may not be able to recognize the patterns, depending on their location and number, we have a situation where, once a pattern hits the grid in one particular location, the detector can either:
- detect it as a pattern of kind A with certainty;
- detect it as a pattern of kind B with certainty;
- infer that a pattern lighting up some pixels is of kind A with higher probability than B;
- be unable to prefer one of the two hypotheses for the pattern hitting the grid;
- infern that a pattern lighting up some pixels is of kind B with higher probability than A;
- fail to respond in any way to the pattern, in case no pixel gets hit.
In other words, we can have true positives and false positives for both hypotheses, as well as cases of no detection. Let us write a utility function that we want to maximize as:
U = [N(A|Atrue)+N(B|Btrue)-N(A|Btrue)-N(B|Atrue)] / Nevents
where Nevents is the total number of patterns hitting the grid, when we assume the patterns fall randomly with a uniform distribution (i.e., every pattern in every location is equally probable). Also, note: Nevents is **not** the total patterns that lit up at least one pixel, as some patterns may lighten up no pixels, if the grid has been instrumented with too few pixels. In the expression above N(A|Atrue) is the number of patterns we assigned to the A hypothesis when in fact they are of type A, and so on.
If you play with this problem you might find it useful to consider a total of Nevents = 18, one of each kind for each of the two patterns: this way you are sampling uniformly by construction from all the possible cases. Then, you will soon realize that in the case N=1 (if you have only one pixel) you should place it in one of the spots marked "A" or "B" below, which provide a utility equal to
U = 2/18; that is because those spots can be lightened up with different frequency by patterns A or B occurring at four different locations. The recipe in that case is to claim that the identified pattern is A or B whenever the chosen pixel is lit up, and the opposite otherwise.
A 0 A 0 A
0 B B B 0
A B 0 B A
0 B B B 0
A 0 A 0 A
The situation becomes only slightly more interesting if you have money to instrument the grid with two pixels, but it also becomes more complex. With two pixels, you may have situations when only one pixel is hit, and you must then decide what is the most probable scenario. In other words you have two different bits of information: the fact that one pixel was hit, and the fact that the other one was not. Again, you can classify the three possible detections (10, 01, or 11, in binary terms) as evidence of one pattern or the other, and the problem of placing the two pixels in the most useful location is a bit more complex. You might then find that a scheme like the one in the table below is useful: in the table, we have one row for each of the possible cases (first pixel hit, second pixel hit, both pixels are hit), and for each of these we can consider how many patterns of type A manifest themselves that way, and how many of type B do. The larger the _difference_ between these two numbers, the better discrimination you have of the two patterns with the considered response map.
0 0 0 0 0
0 1 0 0 0
0 2 0 0 0
0 0 0 0 0
0 0 0 0 0
Pixel hits Number of patterns A Number of patterns B classification
-------------------------------------------------------------------------------------
0 4 4 -
1 2 1 A
2 3 2 A
1 2 0 2 B
-------------------------------------------------------------------------------------
U = 4/18
Let us try with three pixels arranged in the pattern below, which AFAIK is the best performer:
0 0 0 0 0
0 0 1 0 0
0 0 2 0 0
0 0 3 0 0
0 0 0 0 0
This time the matrix of possibilities is much richer:
Pixel hits Number of patterns A Number of patterns B Classification
-------------------------------------------------------------------------------------
0 0 0 -
1 1 2 B
2 5 2 A
3 1 2 B
1 2 0 1 B
1 3 2 0 A
2 3 0 1 B
1 2 3 0 1 B
-------------------------------------------------------------------------------------
U = 10/18
So, which is the most performing pattern with two pixels? And with four? And with five, six,... pixels?
I let you play with this riddle and discover how even the simplest pattern recognition problem hides subtleties and surprising asymmetries...




Comments